當機械設備發生振動時,由于實際轉速、摩擦作用與載荷條件都會發生改變,從而形成不穩定的信號特征。采用變分模態分解(VMD)方法進行處理的過程需綜合運用維納濾波、變分技術與希爾伯特變換方法來實現。目前已有學者采用 VMD 方法開展故障診斷研究,并獲得了較大的研究進展,但使用上述方法時應先設置合適的模態數與懲罰條件,在計算大量數據的過程中會耗費較長時間。還有學者根據傅里葉轉換原理設計了一種新的傅立葉分解(FDM)技術,可以實現由高頻往低頻或由低頻往高頻的特定搜索過程,從而把一個具備非線性與非穩態特征的數據表示成多個本征模態函數。而采用 FDM 方法確定單分量信號不能完全符合瞬時頻率,會引起相鄰模態發生交叉混疊的情況。
由于 IFDM 方法同時包含了 FFT 與自適應頻譜分割技術,利用逆傅里葉變換方法來實現自主重構基函數,從而把一個復雜非平穩信號以自適應方式分解成包含多個瞬時頻率的傅里葉本征模態函數(FIMF),再對各 FIMF 分量瞬時幅值與頻率實施預估,由此獲得各 FIMF 分量邊際譜與初始信號時間頻率的能量分布狀態。設計了基于改進傅里葉分解的齒輪箱故障診斷。把一個復雜非平穩信號以自適應方式分解成包含多個瞬時頻率的傅里葉本征模態函數 FIMF,再對各 FIMF 分量瞬時幅值與頻率實施預估,獲得分量邊際譜與初始信號時間頻率的能量分布狀態。
1、本文方法
改進傅里葉分解方法(IFDM)
采用 IFDM 方法進行處理的目標是根據快速傅里葉變換過程,把包含一定能量的非線性與非平穩信號自主分解成包含瞬時頻率的不同單分量信號,計算式如下:
式中:xi(t)為 FIMF 分量;fi( t)和 Fi(t)為噪聲和剩余信號的變化趨勢,同時分解過程需滿足正交性、完備性、局部性與自適應性要求。
應對 IFDM 方法的以下三個方面進行分析。第一,相對于常規傅里葉與快速傅里葉轉換方式獲得的幅值與固定頻率差異性,利用以上方法進行處理時會使得信號幅度的發生明顯變化,同時也無法保持恒定的頻率狀態,對計算展開過程造成了一定的干擾,因此需對該方法進行一定的優化調整;第二,以傳統方式進行傅里葉轉化與 FFT 重構計算的過程屬于一個整體處理的過程,但上述分析只考慮頻率恒定的條件,并未加入時間因素的影響。IFDM 屬于一個局部概念,包含了恒定的基函數,因此可以將所有函數都通過傅里葉正交基空間進行展開,并且基函數也會發生變化,引起上述現象的原因在于 IFDM 可根據信號局部特性,完成基函數的自適應重構過程。
可以將各 FIMF 瞬時幅值 ai(t)與頻率 fi(t)都表示成時間的函數,由此獲得三維時頻能量分布{t,fi(t),ai(t)},將其表示成 H(f,t)。以下為邊際希爾伯特譜 h(f)計算式:
由于基函數空間是正交基空間,自適應重構過程不會發生頻譜分割集交叉,不影響分解的正交性,避免了模態混疊現象。
故障診斷流程
圖 1 為根據齒輪箱故障診斷流程。離線訓練時,數據完成特征提取器與分類器訓練;在線測試時,利用網絡完成輸入數據分類預測。
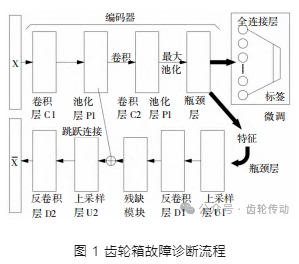
2、實測信號分析
利用 IFDM 方法對滾動軸承內圈故障振動信號分析。選擇 6205-2RSJEMSKF 型深溝球軸承作為測試對象,再對其表面進行電火花加工使軸承表面形成故障直徑為 0.177 5 mm 的故障點,在 0 載荷下控制實驗電機轉速 1793r/min。通過計算得到,轉頻 fr=29.95Hz,同時在內圈中形成的故障特征頻率 fi=162.2 Hz。振動信號形成的時域波形見圖 2。
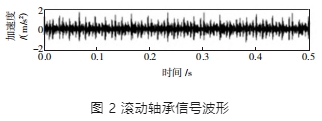
以 IFDM 分解徑向位移參數,按照頻譜將 IFDM 的初始邊界集設定成[15,85,123,178,300]。IFDM 包含了 5 個 IMF 與 1 個剩余項,其中,第一個 IMF 存在明顯調幅調頻的特點,可以從中提取出關于碰摩故障的關鍵數據。計算得到的第一個 IMF 包絡譜與最初的 4 個 IMF 頻譜。
為提取獲得故障特征的相關信號,對 IFDM 的前 5 個初始 IMF 分量包絡譜進行測試。分析圖 3 知,在 EMD 初始 IMF 分量包絡譜內存在內圈故障特征頻率 fi 以及轉頻二倍頻,第 3~4 個 IMF 分量的包絡譜內未形成明顯譜線。以 IFDM 方法計算獲得的前 3 個 FIMF 分量包絡譜內形成了轉頻二倍頻與內圈的故障頻率信號,并且在第 4~5 個 FIMF 分量包絡譜內同樣形成了對應的故障特征頻率,相對 EMD 方法,FIMF 分量形成的包絡譜內含有更少的低頻信號。

3、參數敏感性分析
以迭代損失來檢驗算法的敏感性,引入殘差學習機制的算法損失結果如圖 4 所示。由圖 4 可知,設置殘差后的算法使數據重構誤差快速減小,由此判斷殘差學習方式可以為特征提取與數據重構發揮關鍵作用。
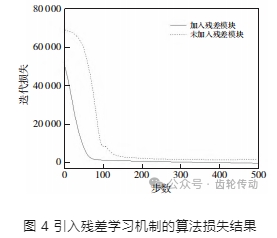
不同卷積核寬度會對振動信號特征提取狀態造成影響,結果見表 1。改進傅里葉分解對各寬度卷積核識別準確性存在差異。隨著卷積核寬度提高至固定寬度后,分類效果不再明顯,且當卷積核設置太大會導致資源浪費。綜合考慮,將第一層卷積層寬度設定在 64 是最優的。
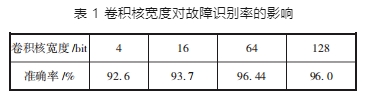
4、結論
本文設計了基于改進傅里葉分解的齒輪箱故障診斷,并開展了測試分析,得到如下結果:對轉子碰摩信號分析可以看到計算得到的第一個 IMF 包絡譜與最初的 4 個 IMF 頻譜;對滾動軸承內圈故障振動信號分析,FIMF 分量形成的包絡譜內含有更少的低頻信號。
參考文獻略.
