加工誤差是影響RV減速器傳動精度的關鍵因素。為評估多種加工誤差對該機構的傳動誤差的影響機制，基于輪齒接觸分析方法構建了考慮齒廓修形、加工誤差和裝配誤差時漸開線齒輪及擺線針輪兩級傳動的輪齒接觸方程，得到不同制造誤差作用下擺線針輪行星傳動誤差分析模型，并評估了各種制造誤差對機構傳動誤差的靈敏度;然后，以該靈敏度為公差等級選擇依據，將RV減速器的各項加工誤差表達為以公差等級IT5和IT6為基礎產生的高斯分布隨機數，通過隨機抽樣誤差來分析各組誤差樣本下RV減速器不發生干涉的可靠度，以及傳動誤差分布情況。計算結果表明：針齒位置度誤差、擺線輪齒距累積誤差對傳動誤差的影響最大;漸開線齒輪偏心量誤差和曲柄軸偏心量誤差的影響較小;針齒半徑誤差的影響最小。將靈敏度較小的加工誤差設為IT6，靈敏度較高的加工誤差設為IT5，可得到所有加工誤差均為IT5時的傳動誤差精度要求，其可靠度達98%且加工成本更低，從而為RV減速器加工精度選用和制造成本控制提供依據。

　　RV減速器屬于擺線針輪行星傳動機構，具有高減速比、高傳動效率、高過載能力且低噪音的優勢，被廣泛應用于工業機器人、機床以及其他高精度傳動領域。

　　RV減速器的制造誤差對其傳動精度有重要影響。國內外學者對擺線針輪機構傳動精度分析主要從3個方面展開：第一類是通過動力學建模和求解的方法獲取傳動誤差;第二類是基于多體動力學和虛擬樣機技術(如MSC.ADAMS軟件)的系統仿真方法;第三類是基于輪齒接觸分析(tooth contact analysis，TCA)方法的研究。

　　動力學方法是研究RV減速器傳動性能的有效途徑之一。集中質量法和動力子結構法是一種建立RV減速器的簡明力學方法，在理論模型的基礎引入誤差因素進行分析，研究各種誤差對RV減速器傳動精度的影響。shan等將RV減速器中輪齒嚙合和軸承支撐用彈簧阻尼代替，同時將各零件的加工和裝配誤差等效到理論模型中，進而分析RV減速器的傳動性能。但是動力學方法在考慮幾何誤差，特別是輪廓誤差方面存在較大難度。

　　此外，在多體動力學及虛擬樣機技術方面，xu 等提出了考慮軸承的擺線針輪傳動接觸模型，采用含接觸的多體動力學架構，對多齒接觸和嚙合特性進行計算，但并未引入加工誤差;吳鑫輝等綜合考慮間隙、加工誤差、裝配誤差、彈性變形等因素建立了虛擬樣機模型并通過實測驗證了虛擬樣機的可靠性;劉華明等在UG環境下建立了RV減速器的三維模型并導人MSC.ADAMS軟件進行多體動力學仿真，并得出了主要加工誤差對RV減速器傳動誤差的影響情況。但是虛擬樣機仿真軟件對含多個接觸環節的模型計算效率很低，為了提高接觸碰撞的求解速度，采用 RAPID幾何引擎。通過三角形或多邊形等幾何圖元拼接擬合物體表面來描述物體三維幾何結構，犧牲了幾何精度，從而無法精確地描述幾何誤差的影響。

　　在TCA方面，Litvin等改變擺線齒輪輪廓既有的向量式表示法，基于齒輪嚙合原理與坐標轉換法，推導出考慮齒廓修形的擺線輪廓的參數式，進而建立完整的TCA流程，并利用該流程求出擺線減速機運轉時的傳動誤差;李軒應用齒面接觸分析原理，建立了有側隙嚙合擺線針輪嚙合副TCA模型及LTCA(Loaded tooth contact analysis)模型，計算擺線齒輪輸出角度及擺線輪輪齒與針齒之問背隙角，得到了有/無負載時傳動誤差、嚙合剛度、傳動比波動等傳動性能指標;Huang 等提出一種基于影響系數法的LTCA方法，首先利用剛體平面運動的瞬時速度中心定理確定接觸點，然后根據赫茲理論與載荷平衡的關系，將多齒接觸問題描述為一個方程組并進行數值求解計算，得到了載荷分布和接觸應力情況。上述研究均未在TCA中融入加工誤差。張也等通過TCA的方法構建考慮齒廓修形、加工誤差和裝配誤差等綜合因素的擺線齒輪齒廓方程，得到多因素綜合作用下的擺線針輪嚙合副誤差分析模型，但是其模型并未涵蓋第一級漸開線齒輪傳動。

　　上述研究表明，針對RV減速器傳動精度分析，虛擬樣機技術存在模型靈活性不足和計算效率低的問題，而動力學方法比較難于融入齒廓幾何誤差因素，以及鮮有實現RV減速器的完整TCA建模與分析。因此，本文根據RV減速器的傳動原理，建立了考慮齒廓修形、加工誤差的TCA法，然后針對各加T誤差對整機傳動誤差的靈敏度進行分析，并以靈敏度為依據對不同零件設置不同公差等級，通過公差等級優化配置，實現滿足傳動可靠度約束的加工質量與成本控制。

　　一、綜合齒廓修形的RV減速器幾何建模

　　漸開線齒廓幾何方程

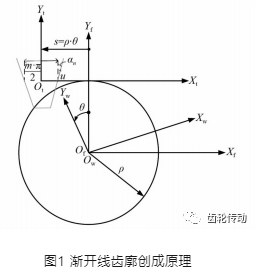
　　RV減速器第一級傳動采用漸開線齒輪的形式。根據漸開線齒形創成法，如圖1所示。圖1中：S_f (X_fO_fY_f)為大地坐標系;S_w(X_wO_wY_w)為漸開線齒輪坐標系;S_t (X_tO_tY_t)為齒條刀坐標系;θ為S_w相對S_f的轉角；s為齒條自大地坐標移動的距離；m為齒輪模數；α_n為壓力角；ρ為節圓半徑；u為齒條刀輪廓位置變量。齒輪齒廓為齒輪坐標上刀具的輪廓形成軌跡，表達式為

　　考慮修形的擺線輪的幾何模型

　　RV減速器的第二級傳動采用擺線針輪傳動形式。針對擺線輪齒廓進行修形，可使擺線輪易于裝配，提升其可加工性能。常見的擺線輪齒廓修形方法有針齒半徑修形、針齒位置修形和偏心量修形。前兩種方法較為常用，因此綜合這兩種修形方法可得到擺線輪齒廓。

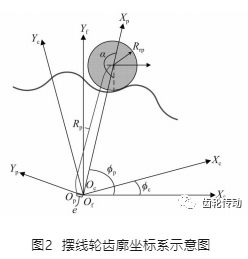
　　擺線輪齒廓坐標系示意圖，如圖2所示。圖2中：Φ_c 為 S_c 的旋轉角度；Φ_p 為 S_p的旋轉角度;R_p為針齒中心到O_p的距離；R_rp 為針齒半徑；P為針齒上與擺線齒輪接觸的一點；α 為P點在針齒上的角度參數；S_c (X_c-O_c-Y_c)為擺線輪坐標系，O_c為原點；S_p (X_c-O_p-Y_p)為針齒坐標系，O_p為原點。其中：O_c與O_f重合；O_P與O_f相距一個曲柄偏心量e。根據嚙合原理，可將擺線輪與針齒視為一對嚙合齒輪，則假定n_c，為擺線輪齒數，n_p為針齒數，二者轉角和齒數符合關系式為Φ_cnc =Φ_pnp。依據此關系式，并考慮針齒半徑修形和位置修形，可得到擺線輪齒廓方程的參數式為r_c=[X_c，Y_c，1]^T，其中

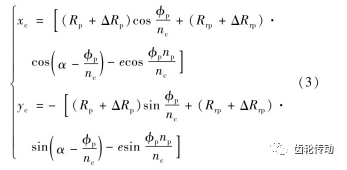
　　式中：ΔR_p為移距修形量；ΔR_rp為等距修形量；α為角度參數，其表達式為

　　在擺線齒輪參數式(3)和式(4)中，參數n。n_p和n_c在設計初期決定減速比后，則不能改動，故而有R_p，R_rp與e可作為擺線輪齒廓修形的依據，通過不同修形參數組合，可達到不同的修形效果。若專門針對修形參數，擺線輪齒廓參數式可簡化為

　　二、RV減速器的輪齒接觸分析

　　輪齒接觸分析的坐標系統

　　RV減速器的第一級傳動為漸開線行星齒輪系。以一個行星輪與太陽輪嚙合為例，如圖3所示。圖3 中坐標系統定義如下：X₁O₁Y₁與X₂O₂Y₂分別為同定在太陽齒輪及行星齒輪上的坐標系；Φ₁為太陽齒輪輸入角(順時針為正)；Φ₂為行星齒輪的轉角(逆時針為正)；Φ_out為行星架的轉角(順時針為正)。

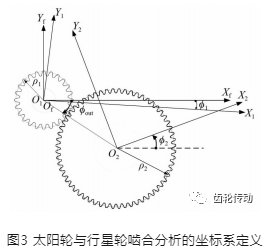
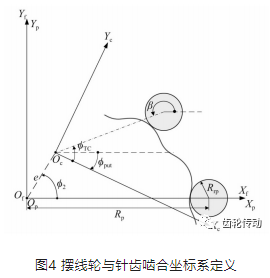
　　RV減速器的第二級采用擺線針輪傳動形式，如圖 4所示。圖4中擺線輪與針齒嚙合如下：Φ_TC為擺線齒輪坐標系中擺線齒輪上接觸點的位置角度參數；β為針齒上真實接觸點的位置角度參數；i為針齒編號，并令最后一顆針齒位于x_p軸上，接著依序命名為第1顆～ 第i顆針齒(逆時鐘方向遞加)。

　　RV減速器的TCA方程構建與求解

　　RV減速器共有兩級傳動，因此必須將兩級傳動過程的齒面接觸方程進行集成，以獲得最終傳動誤差。RV減速器的TCA方程的構建，首先要將幾何接觸模型統一到固定坐標系下。針對第一級傳動，根據漸開線齒廓方程式(1)及相應坐標變換可得到在固定坐標系下的太陽輪齒廓r_f1及行星輪齒廓r_f2的參數式，即

　　式中：M_f1為坐標系S₁向Sf的變換矩陣；M_f2為坐標系 S₂向S_f的變換矩陣。M_f1和M_f2的表達式分別為

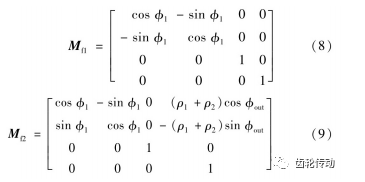
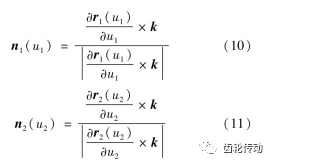
　　針對太陽輪齒廓r₁及行星輪齒廓r₂的參數式進行微分運算，可分別得到其齒廓任一點的切向量，并與垂直XY平面單位矢量k外積后計算出各自齒廓的單位法矢量n₁和n₂，其表達式分別為

　　根據式(10)和式(11)及相應坐標變換可得到在同定坐標系下的太陽輪齒廓及行星輪齒廓的單位法向量，即

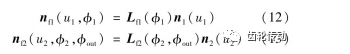
　　式中，L_f1和L_f2分別為太陽輪和行星輪自身坐標系向固定坐標系的變換矩陣，可通過取M_f1和M_f2的前3行與前3列元素得到。

　　TCA的齒面接觸條件：(a)兩齒面接觸點在同一坐標系下的位置矢量必須相同;(b)兩齒面接觸點在同一坐標系下的單位法矢量必須相等，可表述為

　　式(14)和式(15)共包括3個方程，而在輸入角Φ₁確定的情況下，仍有4個未知數。因此，該方程組為不定方程組，仍需考慮擺線輪齒面接觸分析。

　　根據擺線齒廓方程式(5)，經坐標變換得到固定坐標系擺線輪齒廓方程為

　　式中，M_fc為坐標變換矩陣，其表達式為

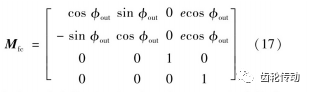
　　類似漸開線齒輪，得到固定坐標系下的擺線輪齒廓的單位法向量為

　　式中：L_fc為由擺線坐標系轉換至固定坐標系的旋轉矩陣；n_c為擺線輪自身坐標系下的齒廓單位法向量，其表達式為

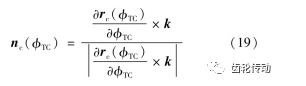
　　第i號針齒外輪廓方程式及外法矢量可分別表示為

　　擺線輪與針齒的TCA方程式分別為

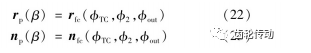
　　綜合漸開線輪齒接觸方程式(14)、式(15)和擺線輪針齒接觸方程式(22)、式(23)，共6個方程，涉及Φ_out，Φ_TC，Φ₂，β，u₁，u₂6個未知數，因此該方程組可解。

　　傳動誤差計算

　　在理想狀況下，RV減速器的輸入角度與輸出角度的比值為定值。當減速器具有傳動運動誤差時，實際輸出轉角并不等于理想輸出轉角。若RV減速器的理論傳動比為z，則根據上述齒面接觸分析后可得具有修形及加工誤差影響的RV減速器的實際輸出角Φ_out其與理想輸出角之間的差值即為傳動誤差ΔΦ_out，如式 (24)所示

　　三、RV減速器的主要加工誤差

　　RV減速器包含諸多零件，如：太陽輪、行星輪、擺線輪、針齒、曲柄軸、軸承及箱體等。其中，標準件的精密度較高，其制造誤差不予考慮，本文僅考慮非標準件的制造誤差，如：第一級漸開線齒輪傳動的零件加工誤差為太陽齒輪偏心誤差、行星齒輪偏心誤差及二者的齒距誤差;第二級擺線針輪傳動的零件加工誤差為擺線輪齒距誤差、針齒半徑誤差、針齒位置度誤差及曲柄軸偏心量誤差等。

　　擺線針輪傳動的主要加工誤差

　　(1)針齒制造誤差：包括針齒半徑誤差d_r、針齒分布位置度誤差R_e和針齒分布角誤差θ_e。將此三種誤差融人式(20)后構成考慮新的針齒廓參數化表達式為

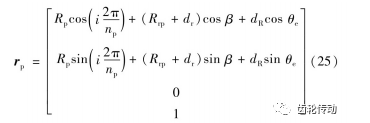
　　(2)擺線齒輪齒距誤差E_pr：如圖5所示，齒距誤差E_pr，可通過式(26)轉化為角誤差θ_c。依據此角度誤差建立旋轉坐標變換矩陣，并且將擺線齒形輪廓參數前乘此變換矩陣，即可得到具有齒距誤差的擺線輪齒形。

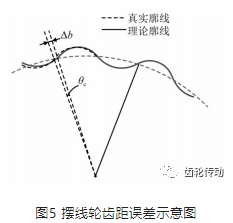
　　(3)曲柄軸偏心量誤差d_ec：將矩陣M_fc的偏心量e 加上誤差d_ec，如式(27)所示

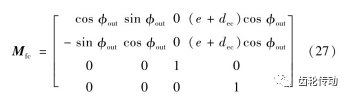
　　漸開線齒輪傳動的主要加工誤差

　　(1)太陽輪偏心誤差：如圖6所示，太陽輪理論中心為O_f，實際中心點為O₁，偏心誤差為d_es。因此可將坐標變換矩陣改為

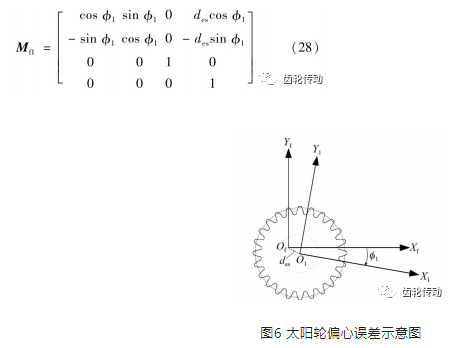
　　(2)行星輪偏心誤差：如圖7所示，行星齒輪中心孔偏心誤差為d_ep，具有誤差的轉移矩陣可以改寫為

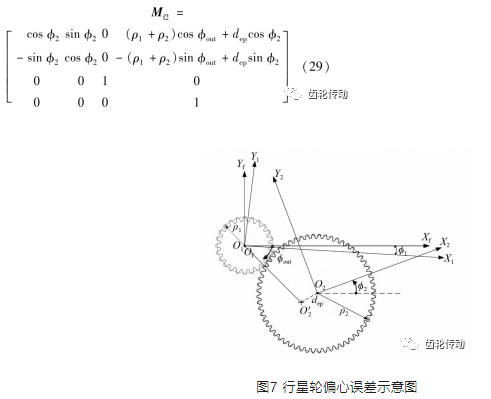
　　(3)漸開線齒輪齒距誤差：太陽輪與行星輪等漸開線齒輪在制造工程中會產生齒距誤差。設定最大累積齒距誤差為E_m，且假定各齒的齒距誤差E_t服從正弦規律，即可表示為

　　式中：n為漸開線齒輪齒數；下標k為s或p，其中，s和 p分別為太陽輪和行星輪;通過弧角關系可將齒距誤差轉換成角度誤差，并以旋轉矩陣的形式疊加到齒形方程式(1)，即可得到考慮齒距誤差的新齒形。

　　各項加工誤差的影響分析

　　依據第2章、3.1節和3.2節所提出的考慮多種加工誤差綜合作用下的傳動誤差計算方法，考察各項加工誤差對傳動誤差的影響。具體的RV減速器設計參數如表1所示。其中，針齒數為11，取較少的針齒數可實現當各項加工誤差發生微小變化時傳動誤差具有較顯著變動，利于分析且不失一般性。

　　(1)針齒半徑誤差dr的影響

　　設定針齒半徑誤差d_r從-0.01 mm增加到 0.01 mm，分析該誤差變化對傳動誤差的影響。針齒半徑對傳動誤差的變化，如圖8所示，基本符合線性關系，即隨著針齒半徑的增加，擺線輪和針齒的間隙變小進而使最大傳動誤差下降，圖8中實線為線性回歸曲線，其斜率即為針齒半徑誤差的靈敏度。

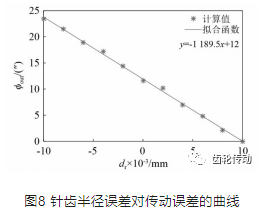
　　(2)針齒位置度的靈敏度

　　分析當針齒分布圓半徑誤差d_r在0～0.01 mm內變化時，傳動誤差的變化情況，如圖9所示。可見，針齒分布圓半徑誤差越大，傳動誤差越大，二者呈線性關系。

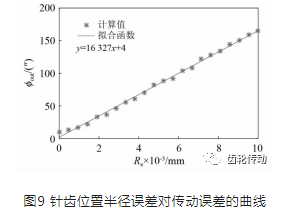
　　(3)曲柄軸偏心量誤差的靈敏度

　　設定曲柄軸偏心量誤差d_ec從-0.01 mm增加到 0.01 mm，分析其對傳動誤差的影響，如圖10所示。可見，隨著d_ec的增大，傳動誤差以近似指數形式增大。圖10所示曲線的斜率并非定值，故而取其梯度即可得到靈敏度及其線性回歸曲線，如圖11所示。

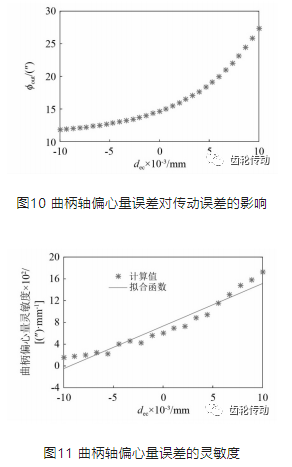
　　(4)擺線齒輪齒距的靈敏度

　　擺線輪的最大累加齒距誤差E_pr變化對傳動誤差的影響，如圖12所示。E_pr在-0.01 mm～0.01 mm內變化。E_pr正負號只會改變起始齒距偏移方向，并不影響整體最大運動誤差，故而成對稱關系。此外，E_pr的絕對值越大，傳動誤差也越大，基本呈線性關系。

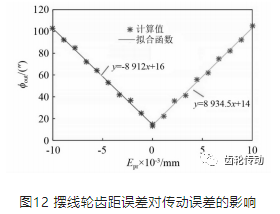
　　(5)漸開線齒輪偏心量的影響

　　RV減速機的太陽輪及行星輪皆為漸開線齒輪，設定二者偏心量誤差在0～0.01 mm內變化，其對傳動誤差的影響如圖13所示。太陽輪與行星輪的偏心量增大均可導致傳動誤差的增大，影響程度大致相同，且均呈線性關系。

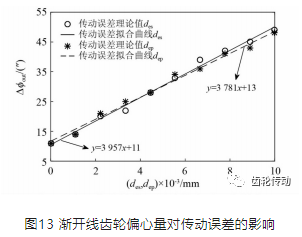
　　(6)漸開線齒輪齒距誤差的靈敏度

　　太陽輪與行星輪的累加齒距誤差E_p1和E_p1變化對傳動誤差的影響，如圖14所示。二者累加齒距誤差在 -0.01 mm～0.01 mm內變化。可見左右兩端如同擺線齒輪齒距誤差約略成對稱之線性關系。

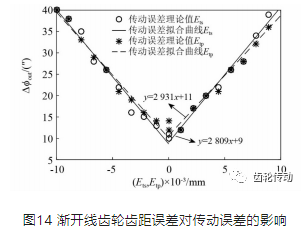
　　加工誤差的靈敏度對比

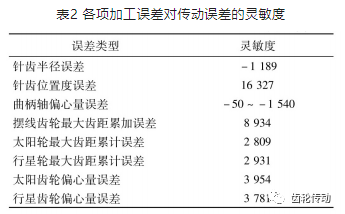
　　將3.3節得到的各項加工誤差對RV減速器傳動誤差的靈敏度匯總，如表2所示。南表2可知，針齒位置度誤差、擺線輪累積齒距誤差的影響較大，而針齒半徑誤差、曲柄軸偏心量誤差、漸開線齒輪齒距誤差及偏心誤差的影響較小。根據各項誤差對傳動誤差的影響程度，可選用不同的加工精度等級，既可保證加工質量，又可控制加工成本。

　　四、基于可靠度的RV減速器加工精度優選方法

　　可靠度分析方法

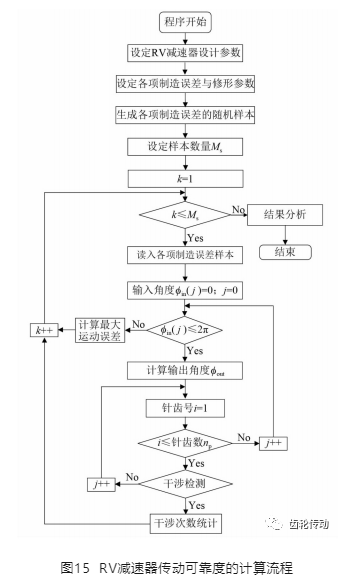
　　根據RV減速器的結構尺寸、各項加工誤差，通過第2章和第3章所構建的傳動誤差分析方法進行可靠度分析。該可靠度分析流程如圖15所示。首先，根據 RV減速器的結構尺寸及加工精度等級，生成給定數量的誤差樣本;然后，針對每組樣本進行十涉分析，若無干涉則繼續進行傳動誤差計算。由于可靠度分析通過隨機抽樣來進行，因此需要足夠大的樣本數才能盡可能降低可靠度誤差。根據文獻，可靠度誤差ε%表示為

　　式中：M_s為樣本總數；p為可靠度。一般情況下，可靠度誤差不超過10%。假定RV減速器的傳動可靠度為 0.98，則可根據式(31)得到該可靠度下所需樣本數為 20 000。因此設定樣本數為20 000組，并計算各組加工誤差下RV減速器在輸入角旋轉360。不會產生干涉的概率，即為該誤差等級下的可靠度。

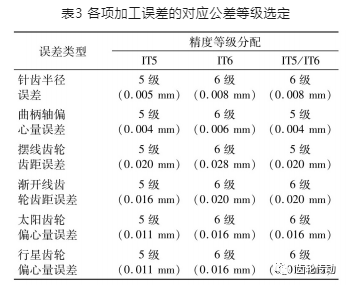
　　當零件批量加工時，其尺寸公差需滿足一定公差等級。加工等級的選用，可綜合考慮加工誤差靈敏度及制造成本。RV減速器為精密傳動機構，故其加工精度設置為IT5和IT6。為了便于對比，公差等級分為三類，即所有誤差均采用IT5、IT6及IT5/IT6混合使用三種情況。基于靈敏度分析結果并依據國際標準公差等級，設定各項加工誤差的等級及誤差尺寸范圍，如表 3所示。因針齒位置度誤差無法通過查表獲得其標準公差，可預設為0.02 mm。雖然曲柄軸偏心量誤差的靈敏 度較小，但對其所連接軸承壽命有重大影響，故設置為 IT5級精度。具體計算時，運用MATLAB軟件中的 “normrnd，'指令來產生符合高斯分布的各零件加工誤差。　　

　　采用隨機抽樣生成的加工誤差來形成設計尺寸，可能會使機構運動時存在十涉。因此，在傳動誤差分析前，需進行十涉檢測。干涉檢查采用距離判別法，即當針齒中心到擺線輪廓上的各個點距離三都大于針齒半徑時，則表示針齒與擺線盤并未接觸;而當針齒中心 到擺線輪廓上有任何一點小于針齒半徑時，則代表針齒和擺線盤發生干涉，具體L的計算方法為

　　因此，可通過計算擺線輪廓到針齒中心最短距離點來作為判定準則。但是式(32)涉及平方及開方運算，在大樣本量的情況下，勢必耗費巨大計算時問。因此，將式(32)進行微分處理得到

　　由式(33)并根據極值定理，得到極值條件下的ΦTC，并將其重新代入式(32)即可得到最短距離。

　　不同公差等級下的可靠度評估

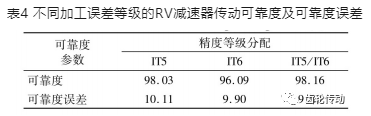
　　以20 000樣本量為基準，針對表3的公差等級，分別進行RV減速器的可靠度分析，結果如表4所示。由表4可知，在IT5以及IT5/IT6混合使用的情況下，可靠度均超過98%;當精度等級為IT6時，可靠度為 96%。可見為了控制加工成本，不必全部零件都采用 IT5級精度，而將對傳動誤差影響較小的漸開線齒輪加工精度降低一個等級，采用IT5/IT6混合使用，也可滿足傳動精度要求。

　　傳動誤差方面，分別在IT5、IT6及IT5/IT6三種情況下的各自20 000組樣本數中，輸入角旋轉360°，在擺線輪與針齒未發生干涉時對RV減速器的傳動誤差進行統計，得到落在某傳動誤差區間且未發生干涉的樣本組數Ns，如圖16所示。由圖16可知，在IT5與IT6 等級下RV減速器的傳動誤差分布并不完全相同。IT5 等級下最大運動誤差集中分布在60”～100”;IT6等級下最大運動誤差集中分布在80”～100”。此外，相對 IT6級，IT5級下傳動誤差整體趨勢較集中，且主要分布在較小區間。

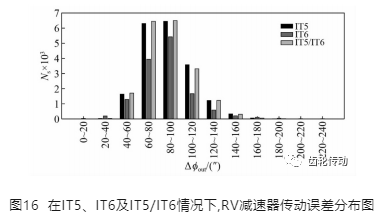
　　在IT5與IT5/IT6兩種情況下，最大傳動誤差分布幾乎相同，可靠度也較為接近。因此，將太陽輪和行星輪的加工等級改為IT6等級后，對RV減速器的傳動精度影響很小。因此在實際加工中，可通過選配不同的加工等級來實現既可滿足傳動要求，又可降低加工成本的目的。

　　五、結論

　　本文以輪齒接觸分析方法構建了考慮齒廓修形、加工誤差等因素的RV減速器傳動誤差分析模型，以及比較各加工誤差的靈敏度，最后提出了在滿足傳動可靠度的前提下，主要加工誤差的公差等級優選方法，總結如下：

　　(1)綜合對比各項加工誤差對傳動誤差的影響，表明針齒半徑誤差、針齒位置度誤差、擺線輪齒距累積誤差、漸開線齒輪偏心量誤差和累積齒距誤差均勻與傳動誤差近似呈線性關系;曲柄軸偏心量誤差與傳動誤差近似呈指數關系。

　　(2)通過對比各加工誤差對傳動誤差的靈敏度可知，針齒位置度誤差、擺線輪累積齒距誤差的影響較大，而針齒半徑誤差、曲柄軸偏心量誤差、漸開線齒輪齒距誤差及偏心誤差的影響較小。

　　(3)當可靠度滿足0.98和可靠度誤差小于10%時，隨機樣本總量需大于20 000。基于該樣本量進行 IT5級和IT6級公差下RV減速器傳動誤差分析，結果表明，漸開線齒輪與針齒半徑采用IT6級精度、擺線輪與曲柄軸采用IT5級精度，可得到與所有零件均采用 IT5級精度下的相同的傳動誤差分布，從而得到不同公差等級搭配可滿足傳動要求，且能降低加工成本的結論。

　　參考文獻略.