航空齒輪等高速齒輪傳動系統中,由于軸、軸承、殼體和齒輪等受載變形以及零部件制造和裝配誤差,易造成齒輪嚙合錯位即齒輪不對中,根據國內外相關文獻統計,由于齒輪錯位即不對中所引起或 與之相關的故障占所有旋轉機械故障的 60% 以上,微小的錯位可能造成系統轉速失穩、振動加劇、齒輪偏載和疲勞破壞等嚴重后果。關于齒輪嚙合錯位,國內外學者進行了較多的研究,就研究方法而言,主要分為解析法和仿真。Shao 等研究了斜齒輪嚙合錯位對齒輪嚙合力的影響。馬輝等研究了修形對嚙合錯位的影響,結果表明,鼓向修形可改善錯位對齒輪接觸應力的影響。Lin 等、Wang 等和 Saxena 等建立了斜齒輪副嚙合剛度計算模型,說明了嚙合錯位對斜齒輪嚙合剛度的影響,但他們的模型均為切齒嚙合模型,模型較為簡單,考慮因素較少。Guan 等和 Wei 等以齒式聯軸器為對象,考慮錯位建立齒式聯軸器數學模型,研究了錯位對輪齒接觸特性的影響,研究結果表明,在錯位情況下輪齒表面由原來的線接觸變為點接觸。Shi 等建立了準雙曲面齒輪轉子系統數學模型,研究軸不對中對準雙曲面齒輪動態響應的影響,結果表明,軸系不對中對速度、轉矩波動等響應產生了較大影響。Zhan建立了嚙合剛度的有限元模型,分析了齒輪錯位對嚙合剛度的影響。Jones 等和 Li運用有限元方法,建立齒輪模型研究了嚙合錯位對齒輪嚙合性能的影響,錯位改變了嚙合力、傳動誤差和輪齒接觸模式,輪齒修形可減小錯位的影響,但他們的建模過程中均未考慮系統各齒輪軸受載產生的彎扭耦合作用對嚙合錯位的影響。
國內外學者在研究齒輪嚙合錯位時,所建立的模型多為切齒錯位模型,模型中未考慮齒輪軸在運轉過程中受載產生的彎扭耦合作用(各軸系柔性) 對嚙合錯位的影響;研究多局限于錯位對齒輪副嚙合剛度、接觸狀態等齒輪自身嚙合性能影響,而錯位對系統振動特性,特別是錯位對應力造成的影響研究較少。針對以上研究不足,本文運用超單元縮聚方法對系統各軸系和齒輪輪齒進行縮聚創建縮聚主節點,實現軸系及齒輪柔性化,結合多體動力建模理論,在各主節點施加約束和載荷,建立了考慮錯位的全柔體單級航空高速直齒輪傳動系統動力學模型,研究了齒輪嚙合錯位對系統影響。
一、嚙合錯位齒輪傳動系統動力學模型
嚙合錯位主要分為 3 種:角度錯位、軸向錯位和徑向錯位,如圖 1 所示,錯位導致齒輪非正常嚙合,進而影響系統動態特性,文獻的錯位試驗研究結果表明,錯位增大了振動位移頻譜中各主頻處幅值,其中角度錯位的增幅更大,因此本文主要研究角度錯位。
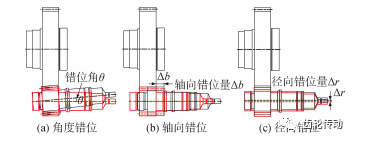
圖 1 嚙合錯位類型
耦合動力學模型基于 Guyan 矩陣縮聚理論完成,通過子結構分析法將結構單元凝聚為一個超單元,大大縮減模型自由度。選取某一部件其動力平衡方程為:
式中:M、K、C 分別為質量、剛度和阻尼矩陣;F 為載荷矩陣;u 為位移矩陣。
u 分為主自由度 um 和從自由度 us,兩者關系為:
式中:T 代表 um 和 us 相互關系,um 和 us 分別用 nm 和 ns 階向量表示,T 為 nm × ns 階矩陣,式(2) 表示為:
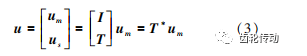
靜態時:
假設部件有 m 個主自由度,且有 s 個從自由度,則式(4)可以表示為:
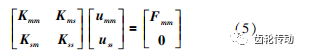
式中:Kmm、Kms、Ksm、Kss 依次為 m×m、m×s、s×m、s×s 階剛度矩陣:主自由度上的載荷向量為 Fmm。
由式(5)可得 :
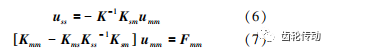
由式(2)、(6)可得:

聯立式(6)、(7)、(8)可得
通過有限元縮聚完成各子結構分析,同時將傳遞矩陣 T 寫入式(1)的阻尼矩陣及質量矩陣中:

主自由度代替了原本結構的自由度,其縮減的自由度動力學方程為:
根據上述建模理論,建立傳動系統動力學模型,流程如圖 2 所示,其中輸入、輸出齒輪參數如表 1 所示,齒輪材料為 9310 合金鋼。
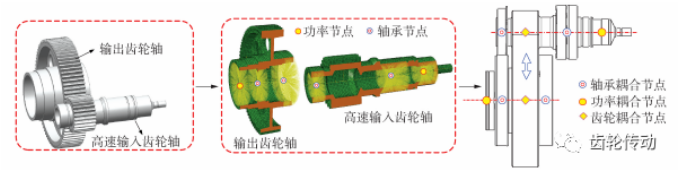
圖 2 節點有限元法動力學建模流程
采用十節點二階四面體單元( Solid187 單元) 對兩齒輪進行網格劃分,劃分過程中對幾何進行簡化(忽略倒角等微小幾何特征) ,保證模型精度兼顧計算效率。高速輸入軸單元數量 80 673,節點數量 134 110,輸出軸單元數量 109 170,節點數量 181 379。
表 1 齒輪參數

在輸入、輸出軸上設置 MPC(柔性多點約束)主節點用以創建多體耦合連接關系。其中輸入軸設置 3 個主節點:1 個功率輸入節點與輸入扭矩建立耦合關系,2 個軸承節點與箱體建立耦合關系;輸出軸設置 3 個主節點:1 個功率輸出節點與輸出轉速建立耦合關系,2 個軸承節點與箱體建立耦合關系。
運用軸承節點建立齒輪軸系與箱體之間的耦合關系,軸承滾動體與內外圈之間的耦合關系為:

運用嚙合節點建立主動和從動齒輪嚙合關系,如圖 3 所示,在每個輪齒節圓位置沿齒寬方向創建均勻分布的縮聚主節點,實現輪齒柔性化建模。
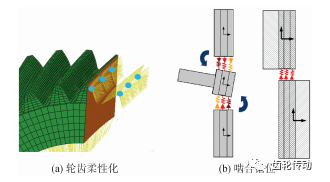
圖 3 考慮嚙合錯位的齒輪嚙合單元
將主節點載荷分布到齒面節點上,可計及輪齒彎曲、剪切等變形影響。另外,該方法可考慮軸系、輪齒瞬時變形、偏斜等導致的嚙合錯位狀態,進而影響系統動態響應。
二、嚙合錯位對系統動態特性影響
齒輪嚙合特性
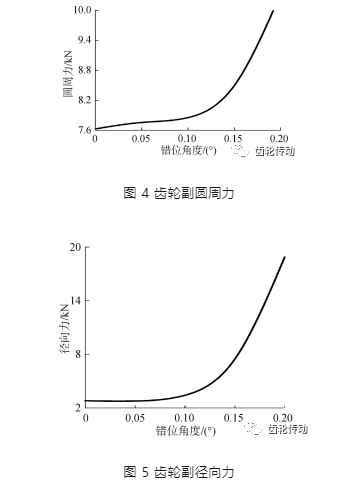
齒輪副嚙合力:多體動力學模型中求解齒輪副所受圓周力和徑向力有效值隨錯位角度變化趨勢如圖 4、5 所示,由圖 4、5 可知,總體上圓周力和徑向力均隨錯位角度增大呈增大趨勢,0. 05°范圍內兩者變化趨勢較為緩和,0. 1°時圓周力和徑向力大小分別為 7 852 N 和 3 418 N 相比于正常情況下的增幅分別為 2. 9%和 21. 8%,錯位角超過 0. 1° 后圓周力和徑向力增幅顯著。
動態接觸應力:考慮齒輪的接觸強度。得到齒輪動態接觸應力可以分析其受力狀態、嚙合情況和沖擊程度等,對研究齒輪嚙合特性至關重要。
嚙合錯位角 θ 從 0°變化至 0. 2°時,齒輪副動態接觸應力隨 θ 變化的時頻域響應如圖 6 所示,齒輪材料為 9310 鋼,屈服強度 940 MPa,正常情況下接觸應力均值是 595 MPa,滿足接觸強度要求。隨著 θ 增大接觸應力明顯增大,這是因為錯位后輪齒接觸面偏向一側,造成偏載。相同時間內應力幅交變頻率更快,加速了材料的疲勞破壞;接觸應力頻譜中主要包含嚙頻及其 2 倍頻、3 倍頻,嚙頻處幅值隨著 θ 增大明顯增加。
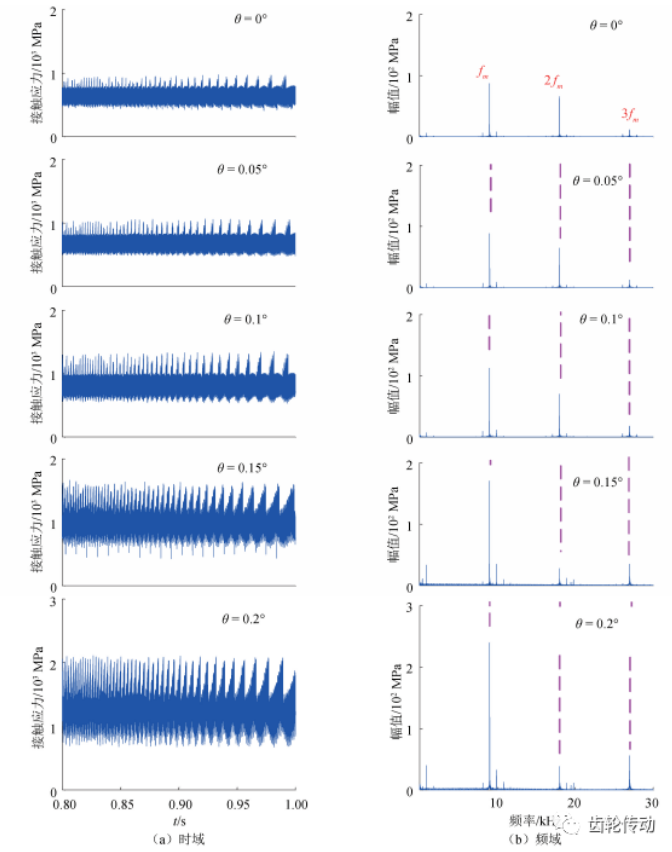
圖 6 接觸應力隨錯位角變化時頻域響應
接觸應力均值和幅值隨錯位角 θ 變化如圖 7 所示,隨 θ 增大接觸應力均值和幅值呈增大趨勢,θ 從 0. 05°至 0. 2° 接觸應力均值分別為 632、762、983、1 247 MPa,相比于正常情況下分別增加 6. 22%、28. 1%、65. 2%、109. 6%;θ 從 0. 05°至 0. 2°接觸應力幅值分別為 620、827、1 235、1 446 MPa,相比于正常情況下分別增加 3. 85%、38. 5%、106%、142%;總的來看,角度錯位對接觸應力影響較大,θ 在 0. 05°內接觸應力增幅較小,超過 0. 1° 后急劇增加,錯位 0. 15°時接觸應力已超過材料的屈服強度。
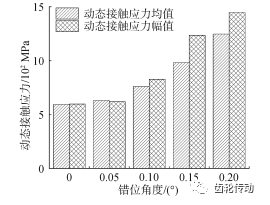
圖 7 接觸應力隨錯位角變化
傳動誤差:傳動誤差峰峰值隨錯位角 θ 變化如圖 8 所示,傳動誤差峰峰值隨 θ 增大呈明顯增大趨勢,θ 從 0. 05°至 0. 2°峰峰值分別為 4. 1、5. 4、5. 8、7. 0 μm,相比于正常情況下分別增加 5. 1%、38. 5%、48. 7%、79. 5%,錯位在 0. 05°內,傳動誤差峰峰值變化較小,超過 0. 05°后增幅加劇。
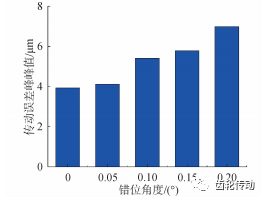
圖 8 傳動誤差峰峰值隨錯位角變化
系統動態特性
振動加速度:錯位角 θ 從 0°增至 0. 2°,拾振點振動加速度隨 θ 變化的時頻域響應如圖 9 所示,振動加速度隨 θ 增大急劇增大;加速度頻譜圖主要包含嚙頻及其 2 倍頻、3 倍頻,嚙頻及其 3 倍頻處幅值隨 θ 增大明顯增大,隨著錯位程度增大最大幅值對應頻率向高頻轉變,θ 為 0. 2°時最大幅值頻率由原先嚙頻的 2 倍頻轉變為嚙頻的 3 倍頻,與此同時由頻域圖可以明顯看出,隨著 θ 增大,各主頻處出現明顯的邊頻帶。
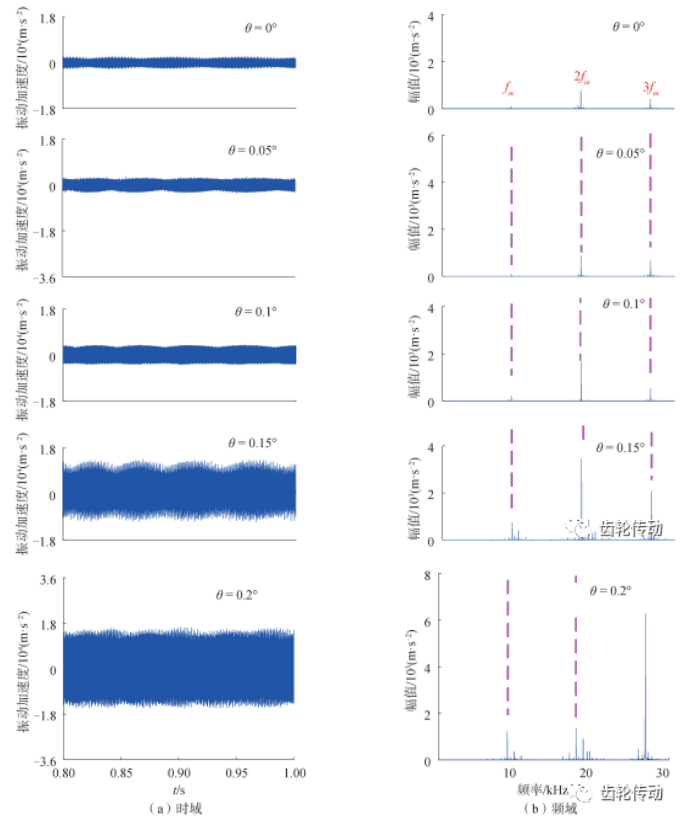
圖 9 振動加速隨錯位角變化時頻域響應
振動加速度 RMS 隨 θ 變化如圖 10 所示,總體來看,加速度隨 θ 增大呈增大趨勢,錯位小于 0. 05° 時振動加速度變化較緩,超過 0. 05°時振動加劇,θ 從 0. 05° 至 0. 2° 振動加速度分別為 1 371. 6、2 192. 5、5 160. 3、8 996. 1 m·s -2,相比于正常情況下分別增加 33. 9%、114. 1%、403. 9%、778. 5%,由此可見,振動加速度對嚙合錯位較為敏感,微小的錯位即可造成系統劇烈振動。
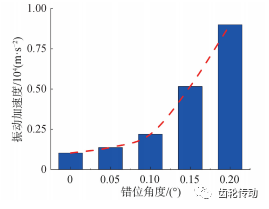
圖 10 振動加速度隨錯位角變化
動應力:多柔體動力學模型結合有限元方法獲取系統動應力(模態應力恢復法),該方法簡單高效適用于絕大多數的機械構件。不同錯位角下,高速輸入齒輪軸動應力云圖如圖 11 所示,未錯位情況下,最大動應力出現在齒輪和軸連接處(應力集中),且軸系動應力隨著錯位角增大明顯增大。
圖 11 不同錯位角動應力云圖
測點動應力時頻域響應如圖 12 所示,動應力隨著錯位角 θ 增大而增大,θ 為 0°和 0. 2°時應力峰值別為 65 MPa 和 165 MPa,增大近 1. 5 倍;頻譜圖中,軸頻處幅值最大,嚙頻處幅值較小但隨 θ 增大其幅值逐漸增大,同時嚙頻處出現大量邊頻帶,θ 為 0. 2°嚙頻處邊頻帶如圖 13 所示。
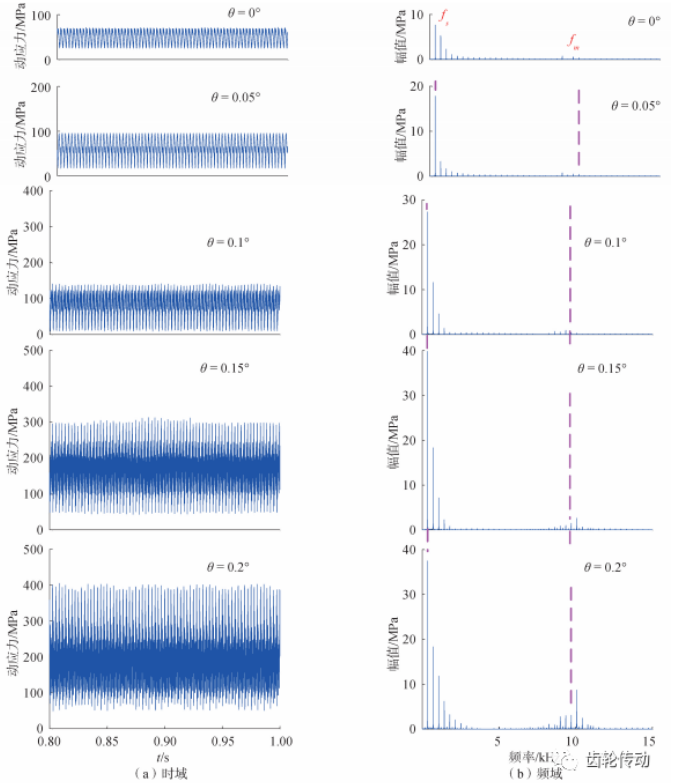
圖 12 動應力隨錯位角變化時頻域響應
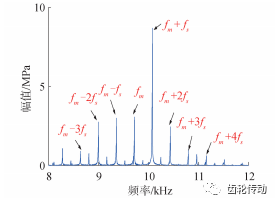
圖 13 θ= 0. 2°時動應力邊頻帶
由圖 13 可知,邊頻帶主要成分為嚙頻和軸頻及其倍頻,該特性可以為系統故障甄別提供思路。
動應力均值和幅值隨錯位角 θ 變化如圖 14 所示,兩者均隨 θ 增大呈增大趨勢,錯位為 0. 2°時動應力均值和幅值較正常情況下分別增大 109. 7%和 441. 3%,動應力增大加速零件疲勞,減少零件壽命;同時由圖 14 可以發現,θ 在 0. 05°內動應力變化較小,θ 大于 0. 05°后增幅較快。
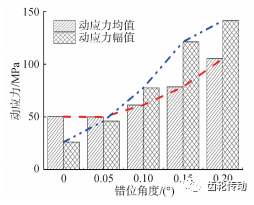
圖 14 動應力隨錯位角變化
三、結論
1) 嚙合力、動態接觸應力和傳動誤差均隨錯位角度增大呈增大趨勢,錯位角度超過 0. 05°后嚙合力、動態接觸應力和傳動誤差峰峰值增幅明顯變大,嚙合性能惡化,其中通常錯位角的范圍控制在 2′ ~ 3′之內以及可通過提高軸承的安裝精度來提高轉配的精度。
2) 振動加速度和軸系動應力隨錯位角增大呈增大趨勢,其中振動加速度對嚙合錯位較為敏感,較小的錯位即可造成系統劇烈的振動;由頻域響應可知,隨著錯位角增大,各主頻附近出現由軸頻及其諧波組成的豐富邊頻帶,該特性可為系統故障診斷提供思路。
3) 高速齒輪傳動系統對齒輪嚙合精度要求極高,較小錯位角度即可導致系統動態特性急劇惡化,對于本系統而言,嚙合錯位角度應控制在極小的錯位角度范圍以內。
參考文獻略.
