風力發電機組運維成本大、對可靠性要求極高，隨著風電機組單機容量朝著8～16 Mw發展，對增速齒輪箱扭矩密度提出了更高要求，由此帶來的齒輪內部接觸疲勞失效問題成為制約傳動系統可靠性的瓶頸。不同于傳統的齒輪接觸疲勞失效形式(如微點蝕、點蝕和剝落)，齒輪內部疲勞斷裂(tooth interior fatigue fracture，TIFF)常見于重載滲碳齒輪，其裂紋源大多位于硬化層與心部交界處，斷裂截面與齒面呈40°～ 50°夾角，主要失效原因包括齒輪次表面等效應力超出材料許用剪切強度、非金屬夾雜物導致應力集中等。
國外FZG、SMT、KISSsoft等研究機構較早開展了TIFF數值模擬和試驗研究;MackAldener等采用有限元方法，研究了齒輪宏觀參數、材料強度、滲碳層深度對TIFF的影響。Al等將TIFF失效計算方法歸納為應力歷程分析、殘余應力分析、多軸疲勞準則選取和失效風險評估四個步驟;Hein等基于材料暴露值研究了不同參數對齒輪內部斷裂失效風險的影響;Octrue等綜合CAE分析方法和多軸疲勞準則，建立了TIFF失效評估模型，并就滲碳層深度和殘余壓應力的影響進行了分析。國內相關研究起步較晚，Liu等建立齒輪內部等效應力模型，通過材料暴露值研究了硬化層深度、殘余應力對齒輪內部疲勞斷裂的影響;zhou等采用彈塑性流體動力潤滑模型研究硬化齒輪的接觸性能，結合DangVan準則研究了表面粗糙度、殘余應力、硬化層深度對齒輪內部疲勞參數的影響。上述研究主要側重于硬化層對接觸性能的影響，而對齒輪疲勞可靠度關注較少。
風電齒輪設計壽命為20～25年，屬典型的高周疲勞范疇。目前風電齒輪的可靠度研究主要針對點蝕和斷齒失效，而針對TIFF失效的可靠度研究鮮有報道。美國可再生能源實驗室早在2007年便率先啟動了風電齒輪箱可靠度相關研究，且一直持續至今;Sun 等基于應力強度干涉模型和Monte Carlo方法建立 了1.5 MW風電齒輪箱可靠性分析模型。秦大同等利用二階矩和攝動法求解風電齒輪動態可靠性指標;陳會濤等應用概率累積損傷理論構建了風電齒輪可靠度模型;劉波等通過建立某1.5 MW風電齒輪箱傳動系統copula可靠性模型，研究了齒輪可靠度隨服役時問變化的規律。目前關于風電齒輪可靠性的研究主要針對點蝕及彎曲疲勞失效，對TIFF失效可靠度缺乏深入研究。此外，大部分研究仍局限于傳統均質材料的理想假設，未考慮風電齒輪時變載荷、硬化層梯度性能以及微觀修形等因素影響，與大模數風電齒輪實際運行場景存在顯著差異，嚴重制約了更高扭矩密度風電齒輪箱的研發。
本文結合某風場2 MW風電齒輪TIFF失效案例，分析影響大模數滲碳齒輪TIFF失效的主要因素，基于應力強度模糊干涉函數和齒輪材料強度退化理論，結合Dang Van多軸疲勞準則建立風電滲碳齒輪內部疲勞斷裂可靠度分析模型，并通過因子試驗和望小優化設計建立TIFF疲勞可靠度優化方法，期望為高可靠性高扭矩密度風電齒輪箱的設計制造提供支撐。
一、齒輪內部疲勞斷裂可靠性分析建模
齒輪內部等效應力
鑒于齒輪接觸過程中的時變多軸非比例加載情況，多軸疲勞準則被廣泛應用于接觸疲勞評估，其中應用較廣泛主要是基于臨界面法的Dang Van準則、Finley準則以及Matake準則等。Dang Van準則認為疲勞裂紋的萌生是由于材料內部的臨界體積內特征滑移帶上晶粒所受的塑形應變引起，靜水應力σH促使裂紋進一步擴展，與TIFF失效中的裂紋萌生擴展較為一致，因此本文采用Dang Van多軸疲勞準則將齒輪次表面應力場轉化為等效應力。風電齒輪通過微觀修形優化齒面載荷分布，首先通過齒輪箱有限元模型提取齒面嚙合線上各點單位長度載荷，則次表面應力場可根據 Hertz接觸理論求解。
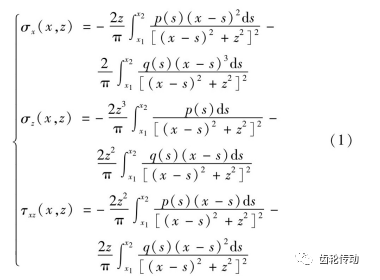
式中：p(s)為齒面壓力分布;q(s)為摩擦力分布;x為沿嚙合線方向坐標;z為沿齒面深度方向坐標，應力分量得出后即可利用Dang Van多軸疲勞準則求得目標點等效應力分布。
式中，材料疲勞參數 
分別為對稱循環下材料的扭轉和拉壓疲勞極限，針對合金鋼風電齒輪， 
，靜水應力σH和最大剪應力τmax根據齒輪次表面應力分量求得。
風電齒輪滲碳熱處理和磨削后不可避免的會引入殘余應力，將顯著影響齒輪接觸疲勞性能，通過考慮等效殘余應力τRS(z)和殘余應力擾動量ΔτRS(z)，對當量應力進行修正
式中，τRS(z)和ΔτRS(z)可通過殘余應力σRS(z)直接求解如下
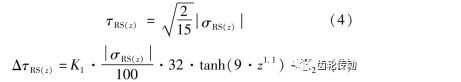
通常齒輪殘余應力可由x射線衍射儀直接測得，也可通過經驗公式近似計算。對于正常狀態的滲碳硬化齒輪，工程實踐中通常采用Hertter經驗公式計算殘余應力
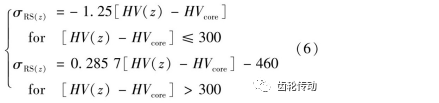
式中：HV為齒輪硬度梯度；HVcore為齒輪心部硬度。
齒輪材料強度及退化
根據Witzig的測試結果，材料質量等級滿足 ISO6336-5 MQ級時齒輪內部任意點許用強度服從以下經驗公式
式中：kτ，per為硬度梯度修正系數，滲碳齒輪取0.4；kml為材料相關系數，對于抗拉強度Rm≥900 MPa的材料，取值1.08。齒輪內部疲勞斷裂失效風險程度可通過材料暴露系數AFF(z)表示
這一系數通過等效剪切應力與許用強度比值表征疲勞失效風險，根據Stahl等研究成果，滲碳齒輪材料暴露系數的安全臨界值為0.8。
材料強度伴隨服役時間增加呈現衰減趨勢，其在任意時問f時的強度被定義為剩余強度，剩余強度的衰減量與材料內部的微觀損傷密不可分。根據等損傷比剩余強度模型，在累積損傷量D的作用下，材料的剩余強度R(n)與初始強度R(0)和循環應力峰值σmax有如下關系
方義慶等基于非線性損傷理論，通過試樣測試確定損傷變量參數，給出基于非線性連續疲勞損傷的疲勞損傷量D的數學描述如下
式中：n為載荷累計循環次數；Nf為材料疲勞壽命，由材料S—N曲線確定，a為材料相關參數，根據文獻取值 1.284。考慮風電齒輪箱中各級齒輪轉速差異，將載荷循環次數n轉換為服役時間t，根據國家能源局發布的統計數據，2020年全國風電平均利用小時數為2 097 小時，則服役時間可轉化為t/2 097年，關于時間的剩余強度模型可以表示為
式中：σmax為應力最大值；Lf可轉化為總服役時間。由于滲碳齒輪鋼通常使用鋁作為強脫氧劑，該過程不可避免的會引入非金屬夾雜物，考慮非金屬夾雜物尺寸影響，材料疲勞循環次數和承受的對稱應力幅的關系可表示如下
式中，areainc為夾雜物直徑，單位為μm，材料相關參數基于18CrNiM07-6齒輪鋼高周疲勞試驗結果取值為：D=5.24×1056、m=22.03、α=-0.28。σ-1為單軸對稱循環疲勞極限，其與材料抗拉極限存在如下近似關系
為獲取滲碳和磨削后齒輪材料實際抗拉強度，從失效齒輪非工作面一側取樣，根據國際標準IS0 6892— 1：2019《金屬材料拉伸測試標準》，按圖1切割拉伸試樣，每片厚度0.9 mm。采用ANS電子拉力試驗機對切片試樣進行抗拉強度測試，得到三條較為規則的拉伸應力應變曲線，如圖1(d)所示，圖1(e)為試樣失效斷口，取三次測試的平均值抗拉強度為Rm=1 196 MPa。
圖1 失效齒輪切片拉伸強度試驗
齒輪內部疲勞斷裂可靠度模型
傳統應力強度干涉理論以極限狀態曲面劃分安全和失效區域與實際存在較大差異，風電齒輪從安全運行到失效存在一個模糊的漸變區，采用降半梯形分布的隸屬函數描述如下
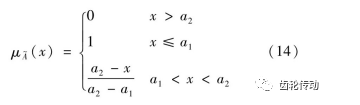
式中： 
為模糊數x的隸屬度；a1和a2分別表示模糊上界和下界。針對齒輪可靠度分析引用擴增系數β確定模糊邊界，βlower=0.75～1.0，βuppre=1.0～1.25，齒輪應力超出材料強度才有可能發生損壞，取βlower= 1.0，βuppre=1.1。考慮齒輪強度退化，令a1=ri(t)，a2=1.1ri(t)，則可得到齒輪模糊可靠度函數
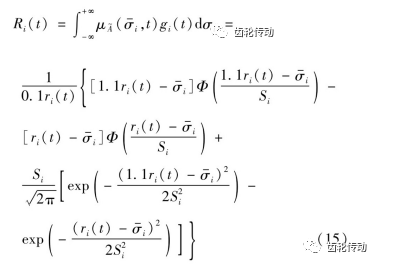
將式(3)、(12)求得的等效應力和剩余強度代人式 (15)，即可得到齒輪內部疲勞斷裂可靠度計算模型如下
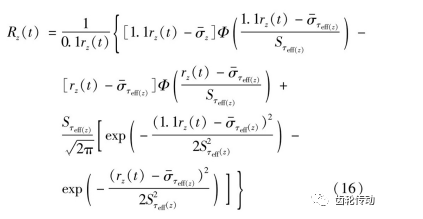
式中：rz(t)代表任意時刻、距齒面深度z點的齒輪材料剩余強度；
分別代表任意點應力標準差和均值。
二、研究對象
某2 MW風電齒輪箱采用一級行星兩級平行軸傳動結構，如圖2所示。
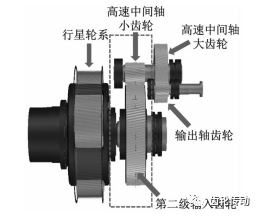
圖2 2 MW風電齒輪箱傳動結構示意圖
該機組失效前累計發電 3 551 347千瓦時，相當于高速中間軸小齒輪額定功率運行1 761.48小時，折合0.84年。失效形式為高速中間級小齒輪內部疲勞斷裂，如圖3所示，裂紋同時朝齒根和齒面兩個方向擴展，在齒面半高處擴展至齒面，表現出典型TIFF失效特征。裂紋源距齒面約3.5 mm，軸向處于1/3齒寬位置。在裂紋源區周圍可以觀察到顯著的貝紋狀推進線，這是由于裂紋在擴展過程中載荷變化或其他應力干擾因素造成裂紋波動，貝紋線的凸起方向即為裂紋擴展方向。
圖3 中間級小齒輪內部疲勞斷裂失效
對圖3齒輪斷口進行掃描電鏡檢查，疲勞輝紋明顯，裂紋源靠近齒頂、存在非金屬夾雜物聚集，圖4(c) 為該齒輪中典型球狀夾雜物光學圖片，夾雜物直徑16 μm。經能譜分析夾雜物主要成分為Al和O元素，與齒輪鋼脫氧環節引入的氧化鋁主要成分類同。
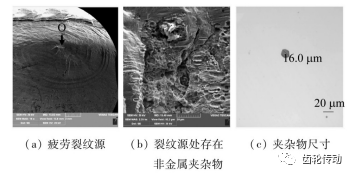
圖4 失效齒輪斷口電鏡檢查
表1 失效齒輪副主要參數
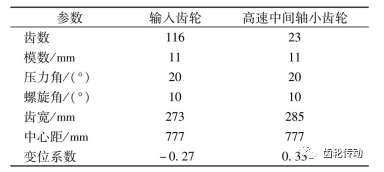
失效齒輪采用1 8CrNiM07-6材料，齒面滲碳淬火處理，該齒輪副額定轉速為384.75 r/min，額定扭矩為 55.89 kN·m，嚙合副宏觀幾何參數如表1所示。該 2 MW風電齒輪箱設計壽命20年，本文基于主機廠家提供的風場載荷譜和Miner法則，采用雨流計數法將風機時問序列載荷等效為44個子工況進行分析，如圖5 所示。
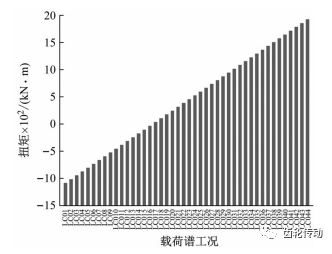
圖5 風場等效載荷譜
三、分析討論
齒輪內部疲勞斷裂危險位置分析
考慮齒輪微觀修形影響，高速中間軸小齒輪在額定扭矩下沿嚙合線單位長度載荷分布如圖6(a)所示，單位長度載荷峰值為1 886.64 N/mm，位于單齒嚙合最高點HPSTC。對嚙合起始點SAP、單齒嚙合最低點 LPSTC、節點PP、單齒嚙合最高點HPSTC、嚙合終止點 EAP材料暴露系數進行分析，結果如圖6(b)所示，最大值分別為0.103、0.593、0.598、0.607、0.220。可見載荷峰值、材料暴露系數最大值均出現在HPSTC點，與失效齒輪裂紋源部位吻合，下文將著重分析該點對應縱深截面上各點的疲勞斷裂失效風險。
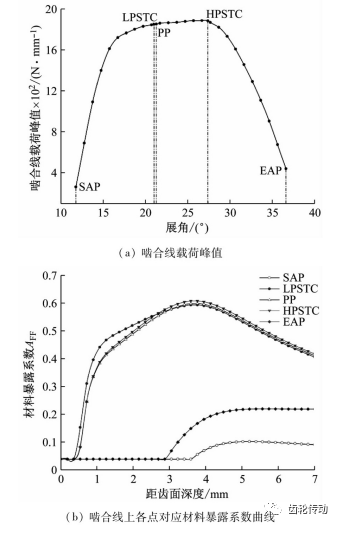
圖6 載荷與暴露系數分布
高速中間軸小齒輪HPSTC點對應的靜水應力σH、 最大剪應力τmax、殘余剪應力τRS(z)和ΔτRS(z)分布如圖7(a)所示，材料許用強度τper與齒輪熱處理后硬度梯度曲線近似分布;疊加殘余應力分布影響后，當量應力τeff在距齒面2.88 mm處達到峰值107.57 MPa。內部疲勞斷裂失效最大風險部位距齒面3.78 mm，如圖7 (b)所示，與圖3失效樣本3.5 mm裂紋源深偏差 8.0%。
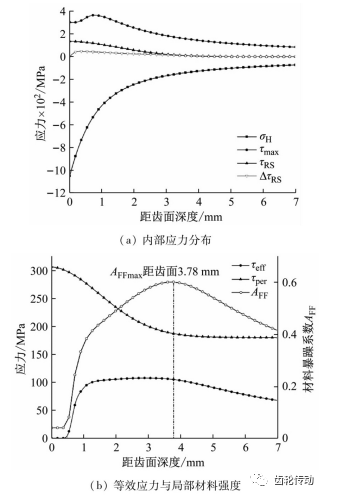
圖7 單齒嚙合最高點應力分布
風電齒輪內部疲勞斷裂影響因素分析
風電齒輪宏觀參數通過增速比、額定扭矩、機艙尺寸等約束，而為適應風電傳動系統載荷多變的特點，需要對齒輪進行特殊微觀修形設計，從而達到優化傳動系統動態性能和齒面載荷分布的目的。失效齒輪采用了圖8所示的齒向鼓形修形、齒向螺旋角修形以及齒端減薄修形。鑒于齒輪宏觀參數針對內部疲勞斷裂失效可調整空間較小，基于前述可靠性分析模型，選取齒輪表面硬度、心部硬度、有效硬化層深度、齒頂修緣、齒向鼓形、齒向斜度6個參數進行因子試驗研究，進行主效應和交互效應分析。采用部分因子試驗設計方法，試驗次數20次，試驗參數如表2所示。其中因素A表面硬度低水平為57HRC、高水平為62HRC;因素B心部硬度低水平為30HRC、高水平為40HRC；因素c有效滲碳層深度低水平為2 mm、高水平為2.4 mm；因素D齒頂修緣低水平為50μm、高水平為120μm；因素E齒向鼓形低水平為0、高水平為40μm；因素F齒向斜度低水平為0、高水平為90μm。
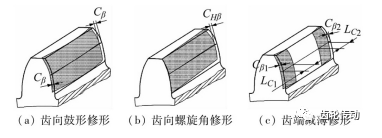
圖8 齒輪常用修形方式示意圖
表2部分析因試驗參數
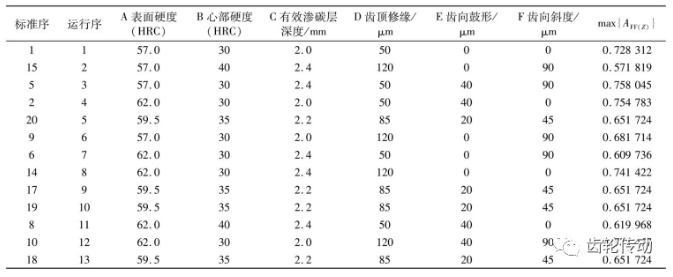
通過因子交互效應各因子對應回歸方程系數的影響，分組為：A表面硬度×B心部硬度、A表面硬度×C 有效滲層深度、B心部硬度×c有效滲層深度、D齒頂修緣×E齒向鼓形、E齒向鼓形×F齒向斜度五組，對存在混雜進行了剔除，相關參數如表3所示。
每種因子組合下材料暴露系數的最大值為 max{AFF,CP(Z)}，各運行序對應的材料暴露系數曲線如圖9(a)所示。對A、B、C、D、E、F、AB、BC、AC、DE、EF 11組因子及其有效組合，采用標準化效應Pareto進行顯著性影響分析，由圖9(b)統計顯著性參考線可知，對材料暴露系數影響顯著性從大到小依次為B心部硬度、E齒向鼓形、F齒向斜度、D齒頂修緣、A表面硬度、EF、AC、DE、AB、BC、C有效滲碳層深度。由式(5)可知，針對給定齒面硬度，心部硬度約大，殘余壓應力越小，對應齒輪內部等效應力越大，故心部硬度對材料暴露系數影響最顯著。齒向鼓形直接影響單位長度線載荷，進而影響內部Dang Van多軸應力，故也對材料暴露系數影響顯著。剩余因子或其組合對材料暴露系數的影響主要也是通過殘余應力和Dang Van多軸應力兩種途徑實現，只是顯著性存在差異。
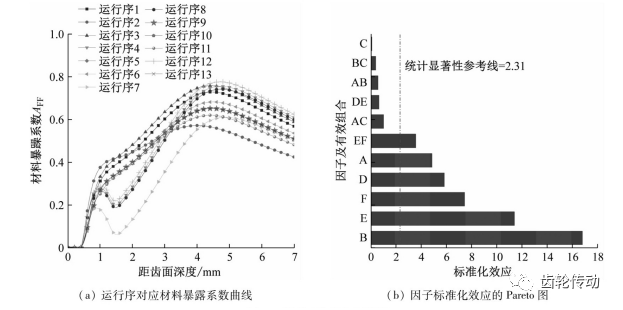
圖9 部分析因試驗結果
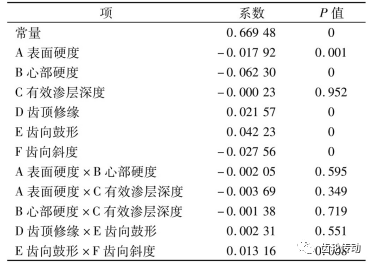
表3 因子主效應及交互效應影響系數
齒輪內部疲勞斷裂可靠性分析及優化
基于風電齒輪失效分析案例，針對齒輪鍛件常出現的氧化鋁類夾雜物，根據GB/T10561《鋼中非金屬夾雜物含量的測定標準評級圖顯微檢驗法》中有關細系球狀氧化物的定義，選取3、5.5、8、16μm四種夾雜物直徑，進行高速中問軸小齒輪TIFF可靠度對比，結果如圖10所示。可見，夾雜物尺寸通過公式(14)影響材料疲勞循環次數，進而影響齒輪TIFF可靠度，影響趨勢呈非線性特點。由圖10(d)可見，失效齒輪含16μm 三氧化二鋁夾雜物，TIFF可靠度經0.32年由 0.999 966衰減至0.968 399，與該齒輪失效時間0.84 年處于同一量級，但理論計算結果偏于保守。
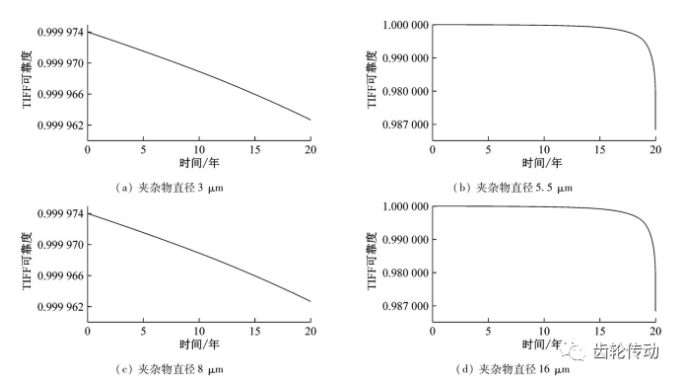
圖10 夾雜物對齒輪內部疲勞斷裂可靠度影響
采用最優化設計方法，對表3獲得的齒輪材料暴露系數回歸方程進行望小優化設計，得到6個主因子最優參數分別為：A表面硬度62HRC、B心部硬度 40HRC、C有效滲碳層深度2.4 mm、D齒頂修緣50 μm、E齒向鼓形0、F齒向斜度90μm。材料暴露系數越小，對應齒輪內部疲勞斷裂可靠度越高。考慮夾雜物直徑為5.5μm時的情況，將優化前后兩組參數代人式(16)，得到可靠度曲線如圖11所示。優化前高速中間軸小齒輪TIFF可靠度初始值為0.999 967，經過20 年運行后變為0.968 399;優化后TIFF可靠度初始值為 1.000 000，經20年運行后變為0.972 678。
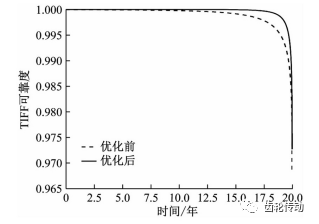
圖11 齒輪內部疲勞斷裂失效可靠度優化
四、結論
(1)基于應力強度模糊干涉函數和齒輪材料強度退化理論，結合Dang Van多軸疲勞準則建立風電滲碳齒輪內部疲勞斷裂可靠度分析模型，通過某2 MW風電齒輪箱高速中間軸小齒輪失效樣本裂紋源深度對比，驗證了模型的適用性。
(2)采用部分因子試驗設計方法，確定對齒輪內部斷裂失效影響權重從大到小的主因子分別為：心部硬度、齒向鼓形、齒向斜度、齒頂修緣、表面硬度、有效滲碳層深度。心部硬度越大、齒向鼓形越小，齒輪內部疲勞斷裂失效風險越小。
(3)針對因子試驗回歸方程進行望小優化設計，獲得風電齒輪內部疲勞斷裂各影響因子最佳匹配參數，優化后20年齒輪內部疲勞斷裂可靠度由0.968 399 提高至0.972 678，本文提出的可靠度優化方法可為高扭矩密度風電齒輪設計提供有益借鑒。
參考文獻略.