行星齒輪變速箱具有傳動比大、承載能力強(qiáng)等優(yōu)點，在現(xiàn)代工業(yè)中得到廣泛應(yīng)用。它們一般在重載和惡劣的工作環(huán)境下工作，其關(guān)鍵部件包括太陽齒輪、行星齒輪及齒圈等，都會出現(xiàn)嚴(yán)重的點蝕和疲勞裂紋。
近年來，許多研究者對行星齒輪變速箱的故障診斷做出了大量貢獻(xiàn)。其中，一批學(xué)者通過動力學(xué)建模與分析研究出齒輪故障、制造誤差和負(fù)載對齒輪箱振動響應(yīng)的影響。Lei等提出了統(tǒng)計指標(biāo)為常數(shù)情況下的行星齒輪箱狀態(tài)監(jiān)測方法。Bartel- mus等提出了非平穩(wěn)運行狀態(tài)下的行星齒輪箱狀態(tài)監(jiān)測。Feng等總結(jié)出行星齒輪箱振動信號的特征頻譜。然而，行星齒輪變速箱一般用于類似風(fēng)力發(fā)電機(jī)組這類運行狀態(tài)不穩(wěn)定的情況，此類情況下，行星齒輪箱振動信號特征為非平穩(wěn)特征。在非平穩(wěn)條件下提取行星齒輪變速箱的時變故障信息較為困難。時頻分析方法因為能有效地揭示時變特征，而常被用于提取非平穩(wěn)信號的故障信息。時頻分析提供了一種可用并且強(qiáng)大的方法用于提取包含重要物理參數(shù)的非穩(wěn)態(tài)信號的瞬時頻率特征。關(guān)于瞬時頻率估計的方法，已經(jīng)有了大量的研究，其中基于時頻分布的瞬時頻率估計方法在處理嚴(yán)重噪聲信號方面具有出色的特性和穩(wěn)定性，因此近幾年獲得了大量的關(guān)注。
為了對瞬時頻率的特征做精確的估計，能否獲得高的時頻分辨率被認(rèn)為是衡量時域分析方法的關(guān)鍵。有3種傳統(tǒng)的時頻分析方法，即短時傅里葉變換、連續(xù)小波變換和魏格納分布。短時傅里葉變換和連續(xù)小波變換應(yīng)用于線性時頻分析領(lǐng)域，這兩種方法通過內(nèi)積來處理信號，并且可以定位時間和頻率。然而，根據(jù)海森伯格不確定原理，這兩種方法都不能同時獲得任意高的時頻分辨率。因此可以認(rèn)為，這些方法在保持良好時間分辨率時僅能保證較低的頻率分辨率，反之亦然。筆者提出的基于快速路徑優(yōu)化的自適應(yīng)短時傅里葉變換(adaptiveshort timefouriertransform，簡稱 ASTFT)方法，希望通過快速路徑優(yōu)化方法獲得瞬時頻率變化規(guī)律來改變時窗長度，從而獲得更恰當(dāng)?shù)臅r頻分辨率。在此基礎(chǔ)上，再次通過使用快速路徑優(yōu)化方法來提高瞬時頻率估計的準(zhǔn)確性。
一、基本原理
ASTFT方法：傳統(tǒng)短時傅里葉變換的時頻窗時寬是固定不變的，但大多數(shù)工程信號的瞬時頻率變化規(guī)律并不恒定，使用時窗固定的短時傅里葉變換處理此類信號效果必然不好。
自適應(yīng)短時傅里葉變換的時窗長度隨瞬時頻率的斜率(即瞬時頻率的一階導(dǎo)數(shù))變化而改變，在瞬時頻率較大時使用短時窗的時頻核函數(shù)，以取得較高的時間分辨率;在瞬時頻率的斜率較小時使用長時窗的視頻核函數(shù)，以取得較高的頻率分辨率。
對于一個純頻率調(diào)制信號，例如：s(t)=eif(t) ，Co- hen給出的最優(yōu)時窗長度和瞬時頻率斜率的關(guān)系如下
其中：f′(t)為瞬時頻率的一階導(dǎo)數(shù)。
當(dāng)對信號s(t)采用變窗高斯核函數(shù)的短時傅里葉表達(dá)式時，時窗長度 Tt 和時變的標(biāo)準(zhǔn)差σ(t)之間的關(guān)系為
結(jié)合式(1)和式(2)可以推出
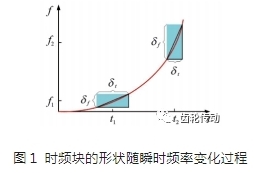
因此，當(dāng)時頻核函數(shù)的標(biāo)準(zhǔn)差參數(shù)σ(t)按照式(3)取值時，變窗高斯核函數(shù)的短時傅里葉變換將會得到最優(yōu)分辨率。舉例說明時頻分辨率與瞬時頻率變化關(guān)系如圖1所示。圖1中：紅線為頻率隨時間變化的時頻脊線;橫坐標(biāo)為時間t;縱坐標(biāo)為頻率 f;圖中矩形為時頻塊。從圖中可以看出時頻塊的形狀隨瞬時頻率斜率變化過程，當(dāng)瞬時頻率的斜率變大時，時頻塊的高度δf 變大，寬度δt 變小，時間分辨率變高而頻率分辨率變低。
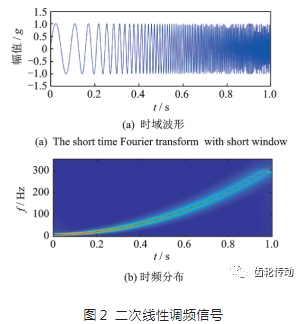
基于快速路徑優(yōu)化的脊線提取： 參考文獻(xiàn)給出了脊線的定義。如 圖 2 所示，使用短時傅里葉變換分析了一個二次線性調(diào)頻信號，左側(cè)為信號時域波形，右側(cè)為信號時頻分布圖，圖中紅色部分是時頻矩陣的極大值序列，其包含了大部分的振動能量，通常被認(rèn)為是時頻分布的脊線。信號由式(4)掃頻得到
其中：瞬時頻率為f(t)=10+300t2。
文獻(xiàn)中給出了一些脊線提取的方法，然而大多數(shù)方法無法準(zhǔn)確恢復(fù)能和信號真實瞬時頻率相匹配的脊線。例如，基于瞬時頻率估計的多項式線性調(diào)頻小波變換方法在處理嚴(yán)重噪聲信號時效果并不好。最明顯的原因是它只考慮時頻分布中每一離散點的最大幅值。所以，筆者采用了一種包含快速路徑優(yōu)化(afastpathoptimization，簡稱 FPO)的瞬時頻率提取方案。該脊線提取方案的具體步驟與原理如下：
1)使用時頻變換方法計算信號的時頻分布矩陣，得到每一時刻的幅值極大值 En(t)，及其對應(yīng)的頻率 Pn(t)
2)通過使用Pn(t)的相鄰節(jié)點 Pn(t)+Δf 和 Pn(t)-Δf 的二次插值對Pn(t)進(jìn)行修正。優(yōu)化方案如下
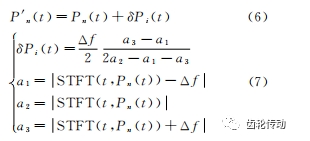
其中：Δf 為時頻矩陣的頻率分辨率;Pn由式(5)計算得出。
3)通過對相鄰時刻極大值點對應(yīng)頻率的差值進(jìn)行懲罰，構(gòu)造極大值點Pn(tm)的權(quán)重函數(shù)
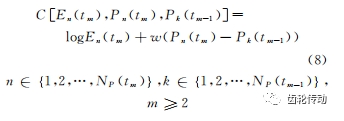
其中：w 為保證Pn(tm)與 Pk(tm-1)之間連續(xù)性的懲罰因子
其中：fs 為采樣頻率;σ為高斯窗函數(shù)的參數(shù)。
因此，使用式(8)的權(quán)重函數(shù)構(gòu)造路徑優(yōu)化函數(shù)如下
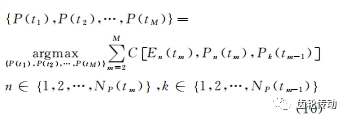
4)通過對上述構(gòu)造的路徑優(yōu)化函數(shù)進(jìn)行求解，得出t1～tm 時刻的最優(yōu)組合{P(t1)，P(t2)，…， P(tM )｝，即為所提脊線。
相對于一些瞬時頻率估計方法，此方案有3個優(yōu)點：①使用二次插值定位幅值極大值的頻率更加的精確;②用來提取脊線的路徑優(yōu)化函數(shù)不僅考慮到脊線當(dāng)前點的幅值大小，還考慮到脊線的連續(xù)性;③快速路徑優(yōu)化的脊線提取方法可以有效地避開隨機(jī)噪點對所提脊線的干擾。
基于快速路徑優(yōu)化脊線的 ASTFT：自適應(yīng)短時傅里葉變換能夠根據(jù)瞬時頻率的斜率自動調(diào)整時窗寬度，從而在瞬時頻率斜率小的時 候保證較高的的頻率分辨率，在瞬時頻率斜率大的時候保證較高的時間分辨率。然而，在對原始信號做 ASTFT 之前，要先進(jìn)行瞬時頻率估計，以瞬時頻率的斜率作為變化時窗的參考。本研究提出了使用時頻分布的脊線來計算瞬時頻率斜率，以此計算自適應(yīng)短時傅里葉變換時所使用的變化時窗。其具體實現(xiàn)步驟為：
1)對原始信號進(jìn)行短時傅里葉變換得到初步的時頻分布S(t，f);
2)對S(t，f)進(jìn)行基于快速路徑優(yōu)化的脊線提取得到f(t);
3)確定自適應(yīng)短時傅里葉變換的標(biāo)準(zhǔn)差參數(shù)
4)以σ(t)為標(biāo)準(zhǔn)差參數(shù)對s(t)進(jìn)行自適應(yīng)短時傅里葉變換得到 ASTFT(t，f)。
二、仿真信號分析
仿真信號構(gòu)造：為驗證所提方法在時頻分析方面的有效性，構(gòu)造仿真信號s(t)如下
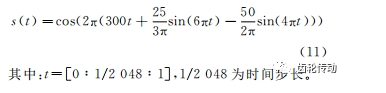
對信號進(jìn)行時頻分析前加入信噪比為 -1dB 的高斯白噪聲。采樣頻率為2048Hz，時域波形如圖3所示，其理論瞬時頻率f(t)如下
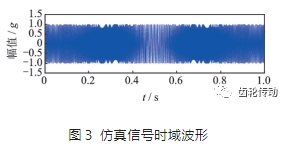
仿真信號分析：通過對s(t)做固定時間窗的短時傅里葉變換，可以看出，在瞬時頻率斜率較大的時候(圖4(a)中紅圈部分)，長時窗的短時傅里葉變換(高斯窗函數(shù)的標(biāo)準(zhǔn)差參數(shù)σ取0.004，σ越小時窗長度越長)效果較差，能量較分散;在瞬時頻率斜率較小的時候(圖4(b)中紅圈部分)，短時窗的短時傅里葉變換(高斯窗函數(shù)的標(biāo)準(zhǔn)差參數(shù)σ取0.04，σ越大時窗長 度越短)效果較差，能量不夠集中。
同時對s(t)做自適應(yīng)短時傅里葉變換(高斯窗函數(shù)的標(biāo)準(zhǔn)差參數(shù)
，如式(3)所示，f(t)為文中所提兩種脊線方法得到的脊線)， 結(jié)果如圖5所示，相對圖4中時頻分布自適應(yīng)短時傅里葉變換獲得的時頻分布能量更加集中。圖 5(a)為基于最大能量峰值(maximumenergypeaks， 簡稱 MEP)的瞬時頻率估計方法做自適應(yīng)短時傅里葉變換所得時頻分布，由于隨機(jī)噪聲干擾，瞬時頻率出現(xiàn)很大的波動;圖5(b)為筆者提出的基于快速路徑優(yōu)化脊線的自適應(yīng)短時傅里葉變換所得時頻分布，由于該方法可以有效降低隨機(jī)噪聲得干擾，得到的時頻分布較為均勻、集中。為從圖5中提取的瞬時頻率與理論瞬時頻率的比較，從圖6可以看出，基于 FPO的瞬時頻率估計結(jié)果更接近于理論瞬時頻率。
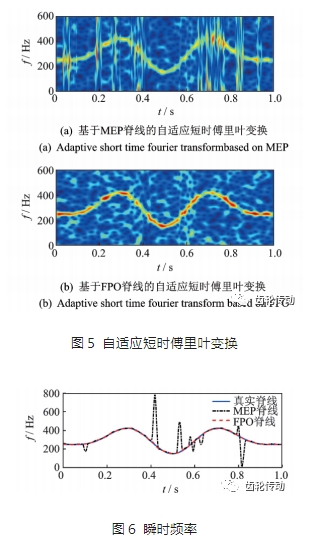
文中通過計算范數(shù)來衡量脊線的精確程度
其中：fTI為真實脊線頻率;fEI為所提取脊線頻率值。
經(jīng)計算可得本算法所得脊線誤差為0.0067，而使用 MEP脊線誤差為0.0361，故本算法所提脊線遠(yuǎn)比 MEP算法脊線準(zhǔn)確。
三、行星齒輪箱故障診斷
行星齒輪箱故障數(shù)據(jù)：本試驗的振動數(shù)據(jù)采集自行星齒輪箱故障模擬試驗臺。如圖7所示，試驗臺包括電機(jī)驅(qū)動、交流電機(jī)、行星齒輪箱、固定軸齒輪箱和制動器。轉(zhuǎn)速傳感器和加速度傳感器分別采集電機(jī)軸轉(zhuǎn)速和行星齒輪箱振動信號，電機(jī)軸轉(zhuǎn)速可由電機(jī)驅(qū)動自由調(diào)節(jié)，本試驗中電機(jī)為變轉(zhuǎn)速，包括一段升速和一段減速過程。信號采樣頻率為12800Hz，采集時長16s。
表1給出了行星齒輪箱的齒輪參數(shù)。由參考文獻(xiàn)提供的星齒輪箱故障階次計算公式如下
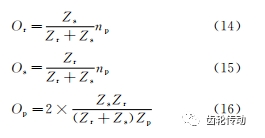
其中：Or，Os 和 Op 分別為齒圈、太陽輪、行星輪故障階次;Zr，Zs 和Zp 分別為齒圈、太陽輪、行星輪齒數(shù);np 為行星輪個數(shù)。
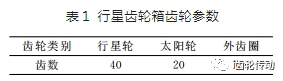
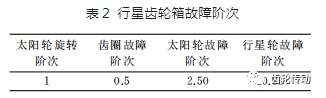
表2為將表1中參數(shù)帶入式(14)～(16)計算得到的行星齒輪箱內(nèi)各零件故障特征階次表。
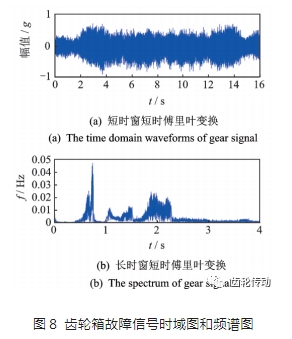
試驗信號分析：通過對含有行星輪裂紋故障的振動信號進(jìn)行階次分析，從而驗證該方法的有效性。行星齒輪箱故障數(shù)據(jù)的振動時域圖和頻譜圖如圖8所示。圖8(a)為試驗中直接采集的振動信息時域圖，圖8(b)為時域信號經(jīng)傅里葉變換得到的頻譜圖，在頻譜中出現(xiàn)了很多峰值，由于齒輪轉(zhuǎn)速波動，很難將頻譜圖中的峰值與故障特征頻率或者故障特征階次聯(lián)系起來。
首先，對原始故障信號使用短時傅里葉變換獲得信號的時頻分布，并提取出信號中電機(jī)轉(zhuǎn)速對應(yīng)的瞬時頻率，如圖9所示，圖中紅線為使用基于快速路徑優(yōu)化的脊線提取方案獲得的瞬時頻率。
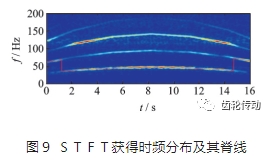
然后，再次對原始故障信號使用筆者提出的基于快速路徑優(yōu)化的自適應(yīng)短時傅里葉變換獲得新的時頻分布，并提取出信號中電機(jī)轉(zhuǎn)速對應(yīng)的瞬時頻率，如圖10所示，圖中紅線為從此時頻分布中提取的瞬時頻率。通過對比，可以看出本方法獲得的時頻分布(見圖10)優(yōu)于傳統(tǒng)短時傅里葉變換得到的時頻分布(見圖9)。將圖9和圖10中提出的瞬時轉(zhuǎn)速信息與實際轉(zhuǎn)速進(jìn)行對比，如圖11所示，圖中曲線1為使用STFT 得到的轉(zhuǎn)速;曲線2為本方法得到的轉(zhuǎn)速;曲線3為實際轉(zhuǎn)速。可以看出通過本方法獲得的轉(zhuǎn)速更加接近于真實轉(zhuǎn)速，可以作為實際轉(zhuǎn)速未知情況下行星齒輪箱故障信號角度域重采樣的參考轉(zhuǎn)速。
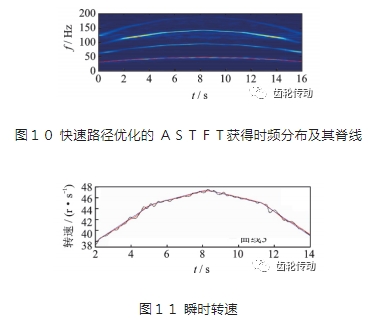
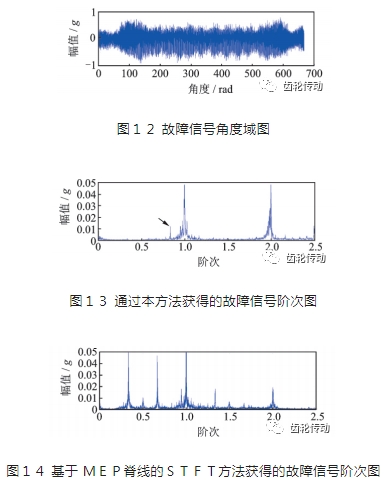
最后，利用獲得的瞬時頻率對故障數(shù)據(jù)重新進(jìn)行角度采樣，即將時域信號對轉(zhuǎn)速進(jìn)行積分從而得到角度域信號，如圖12所示。然后對故障數(shù)據(jù)的角度域信號做階次分析得到振動信號的階次圖，如圖13所示。圖中幅值較大的1階為轉(zhuǎn)頻、2階為2倍轉(zhuǎn)頻。對應(yīng)表2可以在圖13階次中找到故障階次，故障階次為0.83階，幅 值 為0.012g，故障階次非常明顯，從而驗證基于快速路徑優(yōu)化的自適應(yīng)短時傅里葉變換方法在實際應(yīng)用中的可行性。同時添 加如下對比，以通過 MEP 方法獲得的參考轉(zhuǎn)速對信號做階次分析，得到如圖14所示階次圖，從圖中很難判斷出行星齒輪故障階次。
四、結(jié)束語
基于快速路徑優(yōu)化的自適應(yīng)短時傅里葉變換方法依據(jù)快速路徑優(yōu)化方法獲得的瞬時頻率規(guī)律變換時頻窗長度，使自適應(yīng)短時傅里葉變換能夠獲得更加優(yōu)化的時頻分布，從而在下一次的脊線提取過程中獲得更加準(zhǔn)確的瞬時頻率估計結(jié)果。通過對比仿真信號的處理結(jié)果，可以清晰地看出在處理瞬時頻率斜率變化較快的信號時，筆者提出的基于快速路徑優(yōu)化的自適應(yīng)短時傅里葉變換要優(yōu)于傳統(tǒng)的短時傅里葉變換方法。通過使用此方法處理取自行星齒輪變速箱的非平穩(wěn)信號，根據(jù)快速路徑優(yōu)化脊線提取方案獲得的齒輪箱瞬時轉(zhuǎn)速對原始故障信號重新進(jìn)行角度采樣，對角度域故障信號做階次分析，得到明顯的特征階次。通過對試驗信號的分析證明了基于快速路徑優(yōu)化的自適應(yīng)短時傅里葉變換方法在行星齒輪變速箱故障診斷上的有效性。
參考文獻(xiàn)略.