齒向修形可有效地減小齒輪的嚙合沖擊及消除嚙合偏載情況，針對齒向任意修形齒輪的精密加工問題，提出了一種連續展成磨削運動軌跡規劃方法。首先，結合標準螺旋齒面及齒向修形曲線，通過改變端面廓形的螺旋運動軌跡建立齒向修形齒面模型; 接著，考慮左右齒面接觸跡高度差，根據雙面磨削時實際的左右齒面修形量計算對應的 X、Y 軸附加運動量，再將附加運動疊加至砂輪的標準磨削運動軌跡上，建立齒向修形齒輪連續展成磨削的運動軌跡規劃模型; 最后，在蝸桿砂輪磨齒機上開發齒向任意修形功能模塊，并進行對稱齒向修形和任意非對稱齒向修形齒輪磨削實驗，驗證了提出的連續展成磨削運動軌跡規劃方法的正確性。

　　齒輪在實際工程應用中，由于存在著制造誤差、安裝誤差和受載變形等因素，齒輪的嚙合過程會產生嚙入嚙出沖擊、偏載、振動和噪聲等現象。通過對齒輪的齒向進行修形，可以有效地減小齒輪的嚙合沖擊，并降低嚙合時的偏載情況，從而提高齒輪使用壽命。現階段幾乎所有的高速、重載、低噪的齒輪都需要進行齒向修形。修形齒輪加工時的刀具運動軌跡規劃較標準螺旋齒面更為復雜，需要根據齒向修形后的齒面螺旋線規劃刀具的加工運動軌跡，滿足齒面的對稱齒向修形和任意非對稱齒向修形加工需求。

　　齒向修形是指沿齒寬方向有意識地微量修整齒面，使實際齒面偏離理論齒面的修形方法。Walker針對齒輪接觸狀態下的應力集中問題，率先提出對直齒輪進行齒向修形，以此改善其接觸特性并提高齒輪的承載能力。Yoshino 等提出了一種通過補償的方式對砂輪廓形和磨削位置進行調整的方法，實現了齒輪成形磨削時的齒向修形。Shih 等針對五軸數控成形磨齒機，提出了一種高階修正的方法實現齒向修形。在國內，魏延剛等結合齒輪傳動的特點，對漸開線直齒輪進行了齒向修形設計，并使用有限元方法論證了齒向修形可以有效避免齒輪嚙合時的邊緣效應。宋樂明研究了國外鼓形齒的修形標準，給出了鼓形修形量的具體計算公式。郭二廓等建立了齒向修形誤差評價數學模型，通過調整砂輪和工件安裝參數對接觸線進行優化，提高了成形磨齒時的齒向修形精度。汪中厚等根據成形磨齒的嚙合關系，結合實際齒向修形曲線推導了齒面接觸線方程，并利用多組接觸線進行曲面擬合，構建了齒向修形曲面模型。

　　綜上所述，國內外研究學者對齒輪的齒向修形技術已經建立了較為完善的理論體系。但現階段齒輪齒向修形技術的研究重點在于修形齒面的優化設計和分析上，而面向實際的連續展成磨削方法的研究還較少，很難為齒向任意修形齒輪的精密加工提供技術支撐。

　　一、齒向任意修形齒面理論建模

　　標準螺旋齒面建模

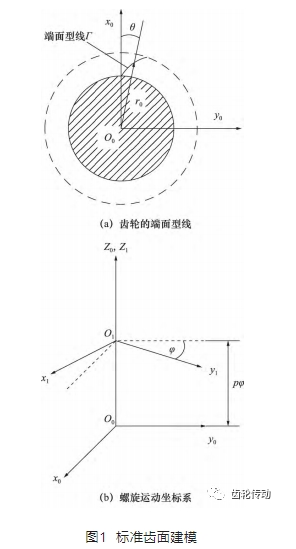
　　從螺旋齒面形成原理出發，建立標準螺旋齒面的方程(圖 1) 。首先在空間建立一個固定的坐標系 S₀ (O₀-x₀，y₀，z₀ ) ，如圖 1a 所示，則齒輪的端面型線 Γ 的坐標方程為:

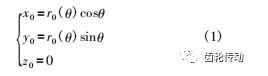
　　式中: θ 為齒輪端面型線的參變量。

　　令端面型線 Γ 繞 z₀ 軸做螺旋運動，即型線繞 z₀ 軸轉動角度 φ 的同時，沿 z₀ 軸移動距離 pφ。此時，端面型線 Γ 在空間上形成的軌跡曲面就是標準螺旋面。圖 1b 中，S₁( O₁-x₁，y₁，z₁ ) 表示型線 Γ 螺旋運動后的坐標系，由 S₀ 到 S₁ 的坐標變換用矩陣為:

　　將式(1) 代入式(2) 得到螺旋齒面表達式

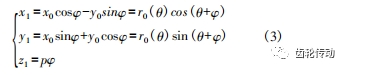
　　式中: φ 為端面型線 Γ 的螺旋運動參變量; p 表示螺旋參數，p =導程/(2π) ，它的意義為型線 Γ 繞 z₀ 軸轉動單位角度的同時，沿 z₀ 軸移動的距離。

　　齒向修形后的齒面建模

　　在建立的標準齒面模型基礎上，對端面廓形的螺旋運動軌跡進行修形，形成齒向修形齒面。齒向修形曲線可以是修正的圓柱螺旋線，或其他的任意修形曲線。由于齒向鼓形修形曲線設計簡單，修形效果較為直觀，故以鼓形修形曲線為例建立修形齒面模型(圖 2) 。

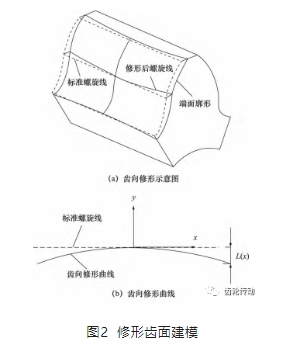
　　圖 2a 表示齒輪端面廓形沿齒向修形后的螺旋線運動形成的修形齒面示意圖，分度圓上的齒向鼓形修形曲線如圖 2b 所示。修形的鼓點為齒寬中部，修形量為 0，齒輪的上、下端面處修形量最大。修形量的大小與齒寬位置的關系函數為:

　　式中: x 為在齒寬方向上的位置; y 表示修形量。

　　根據齒向修形齒面的形成原理，采用附加運動的方式建立修形齒面方程。首先根據齒向修形曲線計算齒輪在齒寬方向上各端截面處的修形量，該修形量為修形前后齒輪端截面廓形的位置偏差; 再根據各截面處修形量的大小改變齒輪廓形的位置，如圖 3 所示; 最終的修形齒面由所有截面上的齒輪廓形構成。

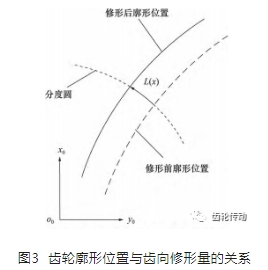
　　齒向修形時，齒輪廓形在標準螺旋運動的基礎上，再附加一個繞齒輪軸線的轉動，轉動半徑為齒輪的分度圓半徑。因為修形量一般較小，可將附加轉動的弧長近似為與修形量對應的廓形移動長度。

　　式中: Φ 為齒輪端面廓形的附加轉動量; r 為齒輪的分度圓半徑。

　　由于附加運動的存在，圖 1b 中，由 S₀ 到 S₁ 的坐標變換矩陣為:

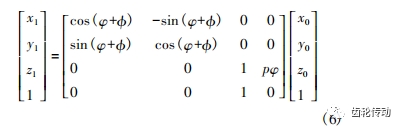
　　聯立式(1) 和式(6) ，得到最終的齒向修形齒面方程。

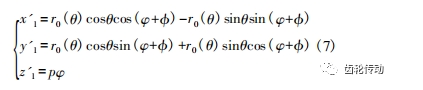
　　式中: x'₁、y' ₁、z' ₁ 表示齒向修形齒面在齒輪坐標系中的坐標值。

　　二、連續展成磨削運動軌跡規劃方法

　　典型的數控蝸桿砂輪磨齒機床結構如圖 4 所示，連續展成磨削齒向修形齒輪時，齒輪的齒向修形可通過改變蝸桿砂輪的磨削運動軌跡實現。蝸桿砂輪沿齒輪的附加徑向運動(X 軸的運動) 及沿齒輪的附加切向運動 (Y 軸的運動) 都可改變包絡出的齒輪廓形的位置。以齒輪分度圓處的齒向修形量為基準，分別討論 X 軸和 Y 軸的附加運動量與齒向修形量之間的關系。將蝸桿砂輪看做是一把齒條刀具，其軸截面廓形近似為直線。

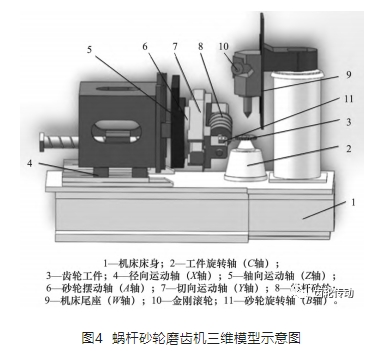
　　圖 5 中，P_a 為齒向修形后的齒輪端截面廓形，P_b 為修形前的齒輪端截面廓形，齒輪在該端截面處的齒向修形量為 δ_n，則對應的齒輪端截面廓形的偏移量為 δ_τ。

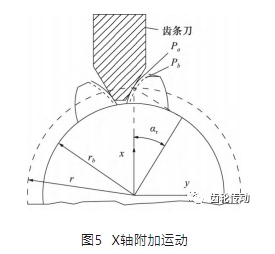
　　則 X 軸的附加移動量 Δx 與修形量之間的關系為:

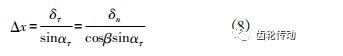
　　式中: β 為齒輪的螺旋角; α_τ 為齒輪的端面壓力角。

　　齒條刀具沿 X 軸方向移動 Δx 后，其左右齒廓相對于齒輪的偏移量相同，因此 X 軸附加移動在齒輪齒槽的左右齒面廓形上產生相同的修形量。

　　(2) Y 軸附加移動量

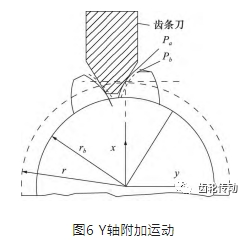
　　圖 6 表示 Y 軸的附加移動與包絡出的齒輪廓形間的關系。則 Y 軸的附加移動量 Δy 與修形量之間的關系為:

　　由于齒輪與齒條刀在分度圓處做純滾動，因此 Y 軸的附加移動量 Δy 等于齒輪端截面廓形的偏移量 δ_τ。由于 C 軸和 Y 軸在齒輪轉動過程中具有定比例的運動關系，可將 Y 軸的附加移動量換算為 C 軸的附加轉動量，產生的修形效果相同。根據齒輪與齒條刀之 間的運動關系，得到 C 軸附加轉動量 Δc 與 Y 軸的附加移動量 Δy 的關系為:

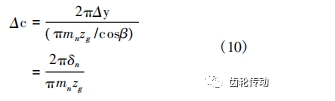
　　由于 Y 軸或 C 軸是沿齒槽的單方向運動，因此 Y 軸或 C 軸的附加運動在齒槽的左右齒面廓形上產生相反的修形量。雙面磨削時，X 軸和 Y 軸(或 C 軸) 的組合運動可同時實現左右齒面任意的齒向修形。

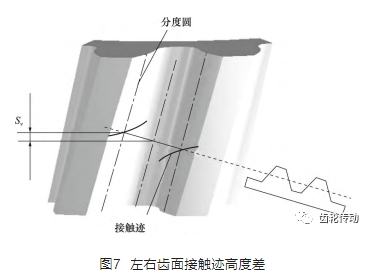
　　蝸桿砂輪與齒輪的嚙合是一對相錯軸螺旋齒輪的嚙合，相錯軸齒輪齒面在嚙合過程中的每一瞬時皆為點接觸，連續展成磨削過程中齒面接觸點的位置連續變化。接觸點的空間運動軌跡為兩個齒面的嚙合線，接觸點沿空間嚙合線的運動在齒面上形成一條接觸跡。蝸桿砂輪運動至齒輪齒寬的不同位置處，均會在齒面上形成一條接觸跡。因接觸跡與齒輪的端截面的夾角始終為 β_b，蝸桿砂輪沿齒輪寬度方向的連續運動在齒面上形成一系列相互平行的接觸跡，所有的接觸跡構成被加工的齒面。當齒輪存在齒向修形時，其修形曲線是疊加在齒面分度圓的齒向螺旋線上，使得分度圓上的接觸點在不同齒寬位置處存在高度差，達到齒向修形的目的。

　　雙面磨削齒輪時，砂輪同時在齒槽的左右齒面上形成接觸跡。由于斜齒輪左右齒面上的接觸跡位置存在著高度差，如圖 7 所示，兩條接觸跡在分度圓處的接觸點沿齒寬方向的高度差為 2S_v。因此砂輪運動至齒輪某一齒寬處，對應的實際左右齒面在接觸跡處的修形量不是左右對稱的。

　　

　　將蝸桿砂輪沿齒寬方向的運動軌跡離散為一系列樣條點，根據每一個樣條點位置處對應的左右齒面分度圓上的實際齒向修形量計算 X、Y 軸附加運動量( 如圖 8 所示) ，擬合所有樣條點形成最終的蝸桿砂輪磨削運動軌跡。

　　圖 8 中，線 1、2 分別表示蝸桿砂輪運動至齒寬中間位置時在左、右齒面形成的接觸跡，兩條接觸跡在齒寬方向的高度差為 2S_v，根據左右齒面分度圓上的齒向修形曲線分別計算出該樣條點處對應的左、右齒面修形量 δ_nL、δ_nR。由前面分析可知，X 軸的附加移動可在左右齒面上形成相同的修形量，Y 軸的附加移動可在左右齒面上形成相反的修形量。因此，X 和 Y 軸的組合運動可同時實現左右齒面任意的齒向修形。在砂輪運動軌跡的每一個樣條點處根據實際的左右齒面修形量計算對應的 X、Y 軸附加運動量，再將附加運動疊加至砂輪的標準運動軌跡上，完成對齒向修形齒輪連續展成磨削的運動軌跡規劃。

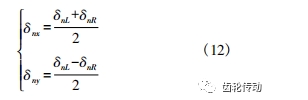
　　三、齒向任意修形齒輪的連續展成磨削實驗

　　為驗證齒向任意修形齒輪連續展成磨削運動軌跡規劃方法的正確性，在開發的蝸桿砂輪磨齒功能軟件上開發齒向任意修形功能模塊，包括齒向修形功能界面開發及磨削 NC 程序編寫。在生產流程模塊下增加齒向任意修形功能界面，用于輸入被加工齒輪的齒向修形曲線，圖 9 為齒向修形曲線輸入界面。

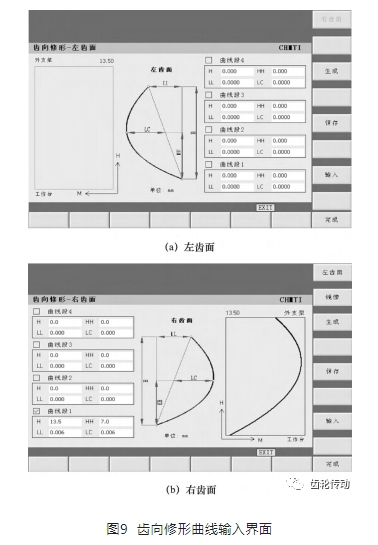
　　利用公式(8) 、(9) 、(12) 計算出蝸桿砂輪在每一個樣條點處的附加運動量 Δx、Δy，將砂輪的附加運動量疊加至標準磨削軌跡上，并生成磨削軌跡樣條程序 (如圖 10) ，砂輪通過走樣條插補的方式實現齒向修形齒輪的磨削。

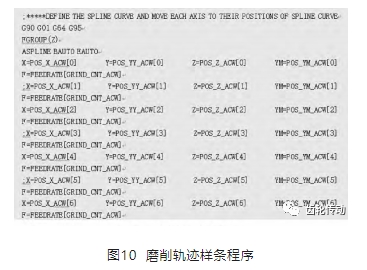
　　圖 10 所示的磨削軌跡樣條程序中，每一個樣條點分別對應一行 X、Y、Z、YM 軸的坐標，其中 Z 軸的坐標從磨削行程的起始點到磨削行程的終止點，X 軸的坐標為對應樣條點處的附加運動量 Δx，Y 軸的坐標為磨削時的砂輪竄刀量( 由磨削對角比決定) ，YM 軸為疊加在 Y 軸上的一根虛擬軸，YM 軸的坐標為對應樣條點處的附加運動量 Δy。

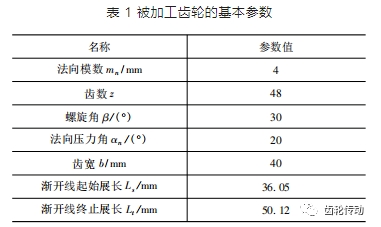
　　實驗選取的被加工齒輪參數如表 1 所示，分別進行左右齒面對稱齒向修形和非對稱齒向修形齒輪磨削實驗。

　　根據設計的齒向修形曲線，在界面上完成對齒向修形曲線的定義，并完成對齒向修形齒輪的磨削加工。被加工齒輪的離線檢測報告如圖 11 所示。

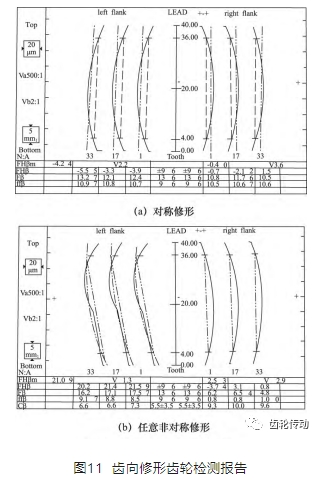
　　圖 11a 為齒向對稱修形齒輪的檢測報告，其齒向修形方式為鼓形修形，左右齒面的齒向修形曲線具有很好的一致性和對稱性。圖 11b 為齒向任意非對稱修形齒輪的檢測報告，左齒面的任意齒向修形曲線是由多段曲線組合而成，右齒面的齒向修形曲線為鼓形曲線。實驗結果驗證了文中提出的連續展成磨削運動軌跡規劃方法的正確性。

　　四、結語

　　針對齒向任意修形齒輪的精密加工需求，在建立齒向修形齒面模型的基礎上，根據齒向修形曲線對連續展成磨削運動軌跡進行規劃，并通過實驗驗證軌跡規劃方法的有效性。

　　(1) 在建立的標準齒面模型基礎上，根據齒向修形齒面的形成原理，采用疊加齒輪端截面廓形的附加運動方式建立了修形齒面方程。

　　(2) 根據修形齒輪的齒向任意修形曲線對蝸桿砂輪的連續展成磨削運動軌跡進行了規劃，建立了齒向修形量與 X 軸和 Y 軸的附加運動量之間的計算模型。

　　(3) 在蝸桿砂輪磨齒上開發了齒向任意修形功能模塊，并通過左右齒面齒向對稱修形和齒向任意非對稱修形齒輪的連續展成磨削實驗，驗證了文中提出的連續展成磨削運動軌跡規劃方法的正確性。

　　參考文獻略.