面齒輪因其傳動結構緊湊、質量小、無軸向定位要求、傳動比大、重合度大、承載能力高和噪聲低等優點,在需要實現較大傳動比的情況下,特別是在航空領域的旋翼機傳動中具有廣闊的應用前景。面齒輪傳動技術目前被美國軍方、NASA 及少數單位和公司掌握,目前國內對于面齒輪的加工技術研究還處于理論和試驗階段,尚無批量生產的面齒輪加工機床。面齒輪軟齒面切齒加工方法主要有插齒、滾齒及基于五軸聯動加工中心的逐點去除法,熱后磨齒加工方法主要有碟形砂輪磨齒和蝸桿砂輪磨齒兩種,上述面齒輪加工方法均存在一定的局限性。
車齒技術最早于 1910 年由 Wilhelm Von Pittler 提 出,蘇聯于 20 世紀 50 年代對車齒加工技術也有過較為深入的研究,但受制于當時機床控制水平和加工精度,未能達到預期加工效果。隨著現代數控機床多軸聯動的實現及控制精度的不斷提高,到 20 世紀六七十年代,國外已經開始將車齒法運用到內齒圈的切齒加工。克林貝格公司和格里森公司分別于 2011 年、2013 年先后研制了圓柱齒輪專用車齒機床,在保證加工精度的同時,極大地提高了生產效率,其效率約為傳統插齒加工的4 ~ 5倍,但相關技術對外嚴格保密。此后,車齒法在國內逐漸得到學者和行業關注,并基于圓柱齒輪的車齒加工,開展了一定的研究工作。
當前的車齒技術主要用于加工內齒圓柱齒輪。為了在國產數控螺旋錐齒輪銑齒機上高效加工面齒輪,文中對面齒輪的車齒加工原理、車齒刀結構設計方法進行研究。通過設計面齒輪車齒刀,結合仿真與實際車齒加工,驗證車齒法用于面齒輪加工的正確性和可行性。
一、直齒面齒輪齒面方程
為了推導直齒面齒輪齒面方程,建立如圖 1 所示的面齒輪和圓柱齒輪嚙合的傳動坐標系。點 O 為面齒輪軸線和與之相嚙合的圓柱齒輪軸線的交點,以該點作為坐標原點,O-X20Y20Z20與 O-X0Y0Z0 分別為直齒圓柱齒輪和面齒輪的定坐標系。O-X2Y2Z2 為固連于圓柱齒輪的動坐標系,其中Z20與 Z2 軸重合,動坐標系繞 Z2 軸轉過的角度為 ?s。O-XsYsZs為與面齒輪固連的動坐標系,Z0 與 Zs 軸重合,動坐標系繞 Zs 軸轉過的角度為 ?2 。
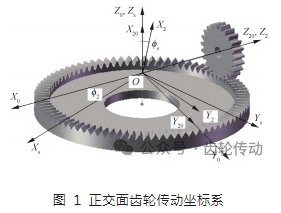
從圓柱齒輪動坐標系到面齒輪動坐標系的坐標變換矩陣為:
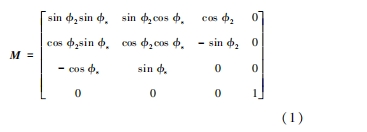
γ2 ,γs 分別為圓柱齒輪和面齒輪的齒面方程,θ0 為圓柱齒輪漸開線的初始夾角,θs 為其漸開線上任意一點的角度參數,us為其齒面的軸向坐標。根據文獻,面齒輪齒面方程應滿足方程組:
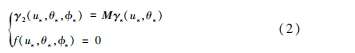
于是在定坐標系 O-X0Y0Z0 下,面齒輪齒面方程為:

式中:θ = ?s ? (θs + θ 0);
rbs ———與面齒輪相嚙合的圓柱齒輪基圓半徑;
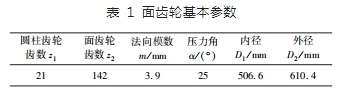
待加工面齒輪基本參數如表 1 所示。
基于面齒輪的理想齒面方程,根據 AGMA 2009— B01標準,將面齒輪齒面劃分為 9×5 共 45 個離散點。面齒輪齒面的過渡曲線,是齒面嚙合區與非嚙合區的交線,以其作為邊界,離散點均取在齒面嚙合區內,如圖 2 所示。

采用 MATLAB 編寫了齒面離散點坐標及法矢計算程序,直接輸入面齒輪基本參數,得到如表 2 所示的標準齒面的坐標及法矢。
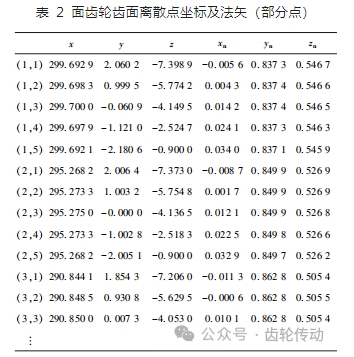
二、面齒輪車齒加工運動模型
正交直齒面齒輪車齒加工的運動模型如圖 3 所示,圖中車齒刀的參考零點設在其端面圓心 A 處。刀具軸線與待加工的面齒輪軸線存在初始偏置距 E,直線 OA 與圖示中面齒輪水平方向直徑的夾角為 λ。
根據幾何關系,偏置距 E 可表示為:
E = R0 sin λ (4)
式中:R0———刀具參考點到面齒輪圓心 O 的距離,即 OA 的長度。
λ 與車齒刀的螺旋角 β 大小相等,并滿足車齒刀切削刃處的螺旋角方向與偏置方向相同。刀具與工件分別按照角速度 ω1,ω2 繞各自軸線旋轉,滿足 ω1 ,ω2 之比為面齒輪和車齒刀的齒數比。同時,刀具以速度 V 沿著 AO 方向進給。A,B,C 分別為面齒輪直徑方向上的 3 個點,車齒刀從徑處開始切入,切入至齒寬中間處和從內徑處切出時的 3 個瞬時位置,VA ,VB ,VC 分別為 A,B,C 處嚙合點的線速度,刀具上嚙合點的線速度為 VT。車齒刀為齒輪刀具,加工過程可視為刀具與面齒輪的無隙強迫嚙合,刀刃每進行一次切削,都會在工件上去除一部分材料。車齒刀和面齒輪對應的嚙合點之間存在相對速度,且隨著刀具不斷靠近面齒輪幾何中心,面齒輪上嚙合點的線速度越來越小,而刀具線速度不變,因此,相對速度也在不斷變化,車齒加工正是 依靠這一相對速度,實現對工件的切削。
設 Z1,Z2 分別為車齒刀和被加工面齒輪的齒數,二者在加工過程中嚴格按照齒數比繞著各自軸線轉動,其關系為:
車齒刀沿 AO 方向進給,速度為 V,可分解為水平和豎直方向上的速度分量 Vx 和 Vy,車齒刀從 A 點運動到 B 點即走過一個齒寬,為一次切削過程。完成一次上述加工之后,刀具沿著工件齒深方向進給一定深度,重復上述切削過程,直到達到齒深尺寸。Vx 和 Vy 進給速度分量大小為:
可見,正交面齒輪的車齒加工運動關系并不復雜,除了主軸的旋轉,只需要 X,Y,Z 方向的線性及工件繞其軸線旋轉這 4 個自由度即可實現。車齒加工運動模型中,必須保證車齒刀和工件嚴格按照傳動比進行強迫嚙合,同時,在嚙合過程中,與面齒輪端平面平行的 2 個線性自由度隨著加工過程,按照一定速度進給。
三、車齒刀結構設計
車齒刀可參考插齒刀具的設計方法,在其基礎上對刀具進行改進,以滿足車齒加工切削運動要求。車齒刀與插齒刀類似,須具備切削角度,同時根據車齒加工運動模型,車齒刀還必須要有螺旋角 β,取值范圍一般為 5° ~35°。車齒刀每個刀齒相當于圓柱齒輪的一個齒,其刀刃切削齒坯過程,可以看成是圓柱齒輪和面齒輪的嚙合過程。為了防止面齒輪與其相嚙合的圓柱齒輪嚙合過程中發生干涉,車齒刀齒數一般比圓柱齒輪多 1~3 個齒。根據車齒刀的結構參數,建立三維模型,用于導入 VERICUT 進行切削仿真驗證。
切削角度
設壓力角為 α0,車齒刀的外圓面為圓錐面,頂刃后角為 αe;齒面兩側為漸開螺旋面,形成側刃后角 αR。車齒刀結構與插齒刀相似,其后角可參考插齒刀的設計方法來確定。如圖 4 所示,車齒刀頂刃后角 αe 為刀具徑向截面中齒頂交線與水平方向上的夾角,側刃后角 αR 為刀齒側面與刀具端面投影垂直的截面之間的夾角。
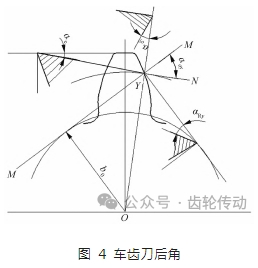
αR,αe,α0 之間的關系如下:
車齒刀具有螺旋角,其螺旋角方向上的后角 αe 與軸向后角 αen之間滿足:
為了改善切削條件,車齒刀需要有一定的前角。取較大的前角對切削條件有利,但是會增大齒形誤差,因此只有在加工精度要求比較低的情況下采用大前角。按照插齒刀的標準規定,前角一般取 γ = 5°,車齒刀可參考該方法進行設計,此時車齒刀的前刀面為內凹圓錐面。同時由于前刀面為圓錐面,側刃也形成了一定的前角。
側刃上任意一點的前角 γn 可按照以下公式計算:
其中,αn 為該點上的壓力角,其計算公式為:
式中:rb,rn———基圓半徑和該點到刀具幾何中心的距離。
由于螺旋角的存在,車齒刀兩側切削角度必有一側是銳角,另一側為鈍角,與之對應的切削刃分別稱為銳邊和鈍邊。在加工斜齒插齒刀時,可在加工刀具前角之前,通過對端面的漸開線齒形進行修正,從而減小由于加工出前角后,以及左右兩側螺旋角不同產生的齒形誤差,因此,可以考慮用插齒刀的刃形修正方法來對車齒刀的刀刃進行類似的修整,以達到減小刃形誤差的目的。
銳邊切削刃的分度圓后角為:
鈍邊切削刃的分度圓后角為:
可見,Δβu = Δβd = Δβ,于是銳邊、鈍邊分度圓螺旋角分別為:
銳邊、鈍邊的基圓螺旋角分別為:
銳邊、鈍邊的分度圓壓力角應滿足下式:

可得銳邊和鈍邊的基圓直徑分別為:

式中:z———車齒刀齒數。
車齒刀設計實例
待加工直齒面齒輪齒數為 142,模數為 3. 9 mm,壓力角為 25°,內、外徑分別為 506. 6 和 610. 4 mm。與之相嚙合的直齒圓柱齒輪為標準漸開線齒輪,齒數為 21,其頂隙系數和齒頂高系數取漸開線齒輪的標準值。根據文中第 2 節車齒加工運動模型可知,在車齒加工中,角度參數 θ 與刀具螺旋角 β 相等。取較大的螺旋角,在切削點會產生更大的相對速度,對切削有利,但同時會增大偏置距,改變刀具切削刃在與其進給方向垂直的平面上的刃形投影,增大齒形誤差。綜合考慮,初步確定刀具螺旋角 β = 10°。根據面齒輪基本參數,可確定車齒刀的基本參數如表 3 所示,再根據齒輪刀具設計方法,計算得到表 4 中車齒刀的各項結構參數。
車齒刀建模
為了更直觀地了解車齒刀的結構,并為后續仿真做準備,結合刀具的各項基本參數及結構參數,在 SolidWorks 中建立車齒刀的三維模型。
由于車齒刀的齒形較為復雜,需要對其各個面進行單獨建模,然后再將各個面剪裁、縫合成實體,如圖 5 所示。
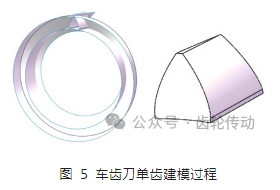
為了便于對整個刀具的建模,將刀具原點設置在端面圓心處。具體過程如下:
(1)分別在端面上繪制齒頂圓、齒底圓、基圓及分度圓,作為構造線;
(2)繪制銳邊對應的基圓及漸開線,并按照基圓繪制螺旋角為 β1 的螺旋線,為便于后續對曲面進行剪裁,其齒向長度應略大于車齒刀單齒的齒向長度;
(3)將銳邊漸開線按照螺旋線進行掃描,形成銳邊及其側后刀面;
(4)根據鈍邊各項參數,重復上述步驟,繪制出鈍邊及其側后刀面對應的曲面;
(5)繪制齒頂及齒底在徑向平面上的交線,通過旋轉,繪制齒頂及齒底的圓錐面,對各曲面進行剪裁、填充、縫合曲面,形成車齒刀單齒的實體模型;
(6)用拉伸和旋轉等方式,建立車齒刀的基體結構,以刀具軸線為對稱中心,將單齒進行圓周陣列,完成對所有刀齒的建模。最后,根據參數將前端面旋轉切除成圓錐面,從而形成刀具前角,如圖 6 所示。
四、基于 VERICUT 的仿真加工
實際車齒過程應分不同切深多次走刀,為了提高仿真效率,僅取面齒輪的 4 個齒槽進行最后一次走刀過程的仿真。面齒輪車齒加工去除材料的過程如圖 7 所示,車齒刀沿著預設路徑,從外向內進行切削,每次切削均在工件上切出一小道溝槽,經過若干次強迫嚙合去除材料,最終形成完整的齒槽。

通過仿真加工中齒槽的成形過程可知,用上述方法設計的車齒刀在加工面齒輪時,銳邊和鈍邊切削順序是不一樣的,銳邊首先接觸到工件,先于鈍邊對工件進行切削,當車齒刀沿齒向方向進給到一定深度后,鈍邊才開始參與切削。刀具最后一次走刀結束,面齒輪加工完成。
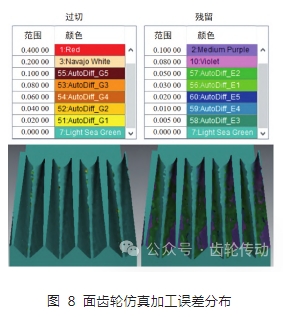
在 VERICUT 中,導入面齒輪理論齒面模型,將仿真加工得到的工件模型與理想面齒輪模型重合,設定不同誤差范圍的顏色,進行可視化比較,得到如圖 8 所示的車齒面齒輪的過切(左)及殘留(右)誤差分布圖。加工后齒面存在少量過切及殘留,且誤差區域呈現非對稱分布,殘留主要分布于靠近內、外徑的齒頂區域;車齒齒面相對于理論齒面無過切現象,但齒面整體呈殘留狀態,靠近齒頂部分殘留量在 0. 05 mm 以上,最大殘留量達 0. 1 mm,而齒面其他區域殘留量主要分布于 0. 3~0. 5 mm,無法達到精度要求。
為了使車齒加工齒面與理論齒面更接近,需要對刀具刃形進行修形,以提高車齒精度。上述仿真顯示齒面整體殘余,應增加車齒刀的齒寬,經過多次仿真切削,得到不同分度圓齒寬和齒頂圓角半徑的仿真結果如表 5 所示。
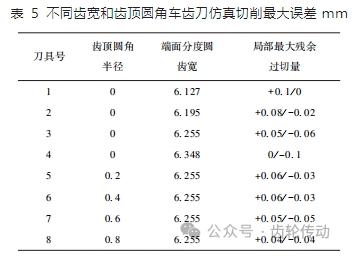
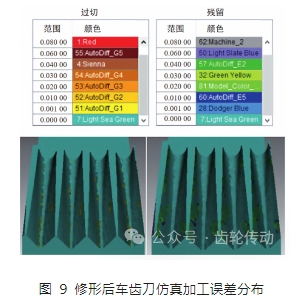
當車齒刀分度圓齒寬取 6. 255 mm,刀具齒頂圓角半徑取 0. 8 mm 時,所得到的加工齒面誤差相對最小,誤差比較結果如圖 9 所示,過切誤差主要分布在齒底和過渡曲面的交界處。另外,圖 9 中左齒面嚙合曲面上存在一個很小的過切區域,區域內的最大過切量為-0. 04 mm,其余齒面的過切量均很小;齒面誤差以殘留為主,主要分布于靠近齒頂和外徑部分,其中最大殘余量為 0. 04 mm,齒面嚙合區上大部分區域的誤差在0. 01 mm以內。
五、實際加工驗證
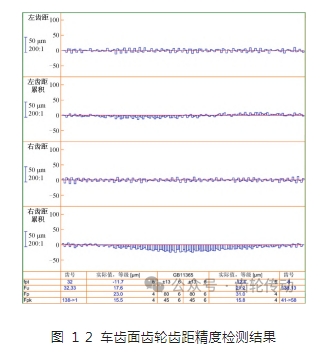
為了驗證面齒輪車齒加工的設計參數、加工參數、車齒刀結構設計及齒面離散點坐標計算的正確性,在長沙哈量凱帥精密機械有限公司的 H650C 螺旋錐齒輪銑齒機上進行了實際加工驗證,如圖 10 所示。在 L65 G 齒輪測量中心進行了齒距精度和齒形誤差檢測,如圖 11 所示。

經過齒輪中心測量,檢測結果如圖 12 所示,根據文獻可知,加工面齒輪的齒距精度達到 DIN6 級。將標準面齒輪離散點坐標文件導入齒輪測量中心,得到實際加工齒面相對于理論齒面的齒形誤差如圖 13 所示。
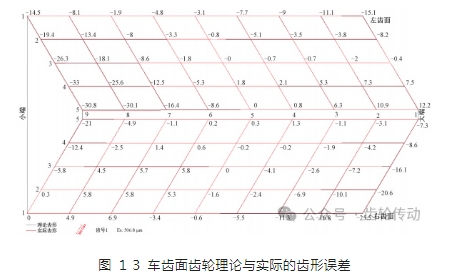
與標準面齒輪齒面相比,左、右兩個齒面最大過切量為-0. 033 0 mm,最大殘余量為 0. 012 2 mm;左齒面靠近大端齒頂部分呈過切狀態,齒底呈殘余狀態,誤差絕對值不超過 0. 016 mm;靠近小端區域整體呈過切狀態,誤差量向小端方向呈增加趨勢,且越靠近齒底的過切量越大,但大端誤差范圍總體比小端的小;右齒面靠近大端區域呈過切狀態,靠近小端區域除邊界外均呈少量殘余狀態,靠近大端齒頂及小端齒底的過切量相對較大,為-0. 025 5 mm,其余部分的齒形誤差絕對值均在 0. 010 mm 以內,與仿真結果基本一致。
六、結論
(1)根據面齒輪齒面方程及相關標準,編寫了參數化的 MATLAB 齒面網格離散點計算程序,輸入面齒輪基本參數可生成標準齒面的檢測文件。
(2)基于面齒輪車齒加工運動模型,確定面齒輪車齒加工重要參數,為加工程序的編寫提供依據。
(3)在插齒刀設計的基礎上,結合漸開線圓柱齒輪車齒刀的設計方法,計算得到面齒輪車齒刀的結構參數,并對車齒刀進行建模和仿真。
(4)采用 VERICUT 軟件構建機床、編入數控加工程序,進行了面齒輪車齒仿真加工,基于初步仿真結果,以車齒刀分度圓齒寬和齒頂圓角為變量,對刀具進行了優化,以提高仿真加工精度;優化后車齒刀的齒面局部齒面誤差最大過切量為-0. 04 mm,靠近大端齒頂的齒面最大殘余量為 0. 04 mm,嚙合區大部分齒面與理論齒面之間的誤差基本均在 0. 01 mm 以內。
(5)文中進行了面齒輪實際車齒試驗。根據齒面離散點劃分標準,在實際測量中確定齒面離散點測量區域時,由于邊界相對于整個齒面必須具有一定的縮進量,因此將避開大端齒頂的殘留區域。面齒輪在齒輪測量中心的測量誤差結果顯示,最大過切量為-0. 0330mm,最大殘留量為 0. 012 2 mm,與仿真結果基本一致,證明了面齒輪車齒刀設計方法及對應車齒加工的正確性。
參考文獻略.
