刮齒技術作為一種高效、環保的齒輪加工技術,在 21 世紀得到了越來越多的關注。在這項技術方面,20 世紀初便有人提出這一設想并獲得專利。然而這種方法在當時并沒有付諸實踐,因為刮齒技術對當時的刮削刀具提出了很大挑戰。Kojima在 1974 年對生產方法進行了研究,根據齒廓分析理論分析了切割器與直齒圓柱齒輪之間的幾何關系,并對刮削刀具的游隙角進行了數值研究。隨著傳動系統的數控裝置、剛性電子齒輪箱、復雜的刀具幾何形狀及快速涂覆技術的進化,動力切削由于其高生產率和靈活的替代性逐步占據了先進技術的市場。德國 Primulter GMH & Co.KG 機床公司于 2006 年提供了 S240R 磨床。長沙機床有限公司 2010 年度開發了切片機 YK1015A。Gleason 在 2013 年出產了動力刮削機 600 PS。刮齒刀是車削齒輪加工系統的重要組成部分,刀具參數和加工參數的合理組合是充分發揮這一技術優勢的保障。關于刮齒的理論研究與技術尚處于比較落后的階段,暫無公開發表的文獻,但是由于刮齒的切削造就了齒輪齒面的形成,因此,文中主要從齒面形成過程來對刀具參數優化展開研究工作。從工程實際可以看到,用于加工內齒輪的動力切削過程比成形更快,并且削屑的連續切削能力遠比拉削更靈活。數值計算工具的興起極大地促進了刮齒技術的發展,Spath 等將動力刮削作為現代齒輪加工解決方案,闡述了動力刮削過程的經濟環保,隨后利用試驗表明了其優勢和發展潛力。Schulze 等和 Hartmut 等針對齒輪動力刮削提出了一種半精削的方法和裝置。王愛群等通過旋切法建立刀具運動模型,針對提高齒輪加工精度提出了“兩步”加工法和刀具選擇的注意事項,并驗證了其所提方法的有效性。
由于現在關于刀具參數與加工參數的優化方法缺乏科學的理論依據,導致最優參數的確定有一定的困難。因此,文中首先建立了刮齒刀運動數學模型,通過對相對速度的推導對刀具工作角度進行定義。在此基礎上,建立理論齒面和加工齒面之間的誤差模型,討論干涉判斷刀具參數方法,最后利用正交試驗法選擇恰當的刀具參數與加工參數來提高加工精度。因此,切削速度取決于電機的轉數和軸角。
一、刮齒切削原理
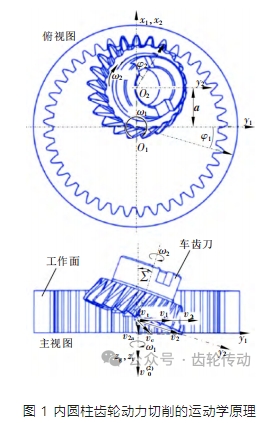
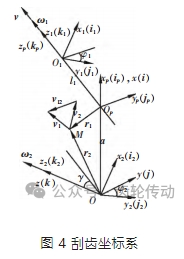
刮齒是通用齒輪制造中的一種連續切削方法。在這種制造技術中,它與一般的車刀和刮刀不同。切削過程是由刀具與工件之間的相對速度引起的。刀具相對于工件放置在橫軸角度上,類似于剃須過程,并且刮齒動作是由刀具和工件之間的相對速度引起的。相對于內齒輪的刮削刀具的幾何結構如圖 1 所示。將笛卡爾坐標系 S1(O1-x1y1z1)和 S2(O2-x2y2z2)分別假設為工件和刮齒刀的運動坐標系,且工件與刮齒刀之間為剛性連接。在圖 1 主視圖中可以得出,內齒輪在 S1 坐標系中進行定位,其旋轉軸與 z1 共線。而刮齒刀則在 S2 坐標系中進行定位,其旋轉軸與 z2 共線。刀具中心通過矢量距離 a 定位在 xy 平面中心,齒輪和刀具的節距圓在圓周的最低點進行切向接觸。同樣,在圖 1 俯視圖中對工件軸和刮齒刀軸構成的刀具工作角度進行了示意。以直齒輪為例,軸向進給速度 v(2)0 與 z1 共線,假設工件運動角速度和刀具運動角速度分別為 ω1 和 ω2。隨著軸向進給 v(2)0開始,工件繞 z1 旋轉 φ1,刀具繞 z2 旋轉 φ2。在滾動刮齒過程中,利用工件和刮齒刀具相對運動使得切削速度 vc 形成定位約束。如圖 1 所示,刀具速度 v2 被劃分為軸向速度 v2a 和切向速度 v2t。然后,切向速度 v2t 和工件運動速度 v1 耦合得到切向速度 vt。因此,切削速度 vc 由軸向速度 v2a 和切向速度 vt 引起。在加工斜齒輪的情況下,行程運動中取 z1 軸方向作為進給方向,但增量角速度 Δω1 依賴于軸向進給,必須添加到 ω1。工件的增量角速度 Δω1為:
式中:mn——工件齒的法向模數;
zg——工件的齒數。
工件與刀具的角速度與軸向進給速度之間的關系滿足:
式中:zt——刮齒刀齒數。
相反,如果工件提供增量運動,則關系可以表示為:
二、刮齒加工理論誤差討論
理論刮齒面數學模型
假設進給導程為 Pz,理論刮齒面即在加工過程中刮齒刀沿工件軸線進給所構成的漸開螺旋面。所以,刮齒刀沿軸線的進給量與導程之間存在線性關系:
如圖 2 所示,在工件坐標系 S1(O1-x1y1z1)中,理論刮齒曲線的極坐標為:
式中:θL——進給極角;
ρ——極徑。
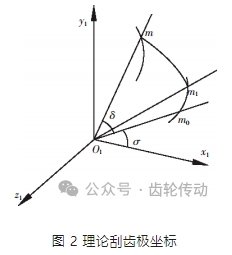
假設理論刮齒面上刮齒邊緣存在某一特定的點 m0 的極徑為 ρ0,進給極角為 θL0,ρ0 與刮齒刀坐標系 S2(O2-x2y2z2)中 x2 軸的夾角為 σ;刮齒邊緣其余任意一點 m1 的極徑為 ρ,進給極角為 θL,則∠(ρ,ρ0)=θL-θL0,且∠(ρ,x2)=σ+θL-θL0。隨著刮齒刀運動轉角為 ξ 時,刮齒刀自身相當于沿 z1 方向移動 pξ,因此,理論刮齒面參數方程描述為:

將 ρ0 與 x2 軸的夾角為 σ0 時作為刮齒起始點,u 為刮齒邊緣參數,且 σ0+u=σ+θL-θL0+ξ,對式(6)進行簡化描述:

實際刮齒與理論刮齒誤差模型
實際刮齒面與理論刮齒面誤差模型進行討論時,首先將一個理論刮齒面作為參考標準。為了確定目標理論刮齒面,可以通過最小二乘法對曲面進行擬合,討論刮齒面上某一點與其鄰近刮齒面之間的距離,從而確定加工誤差。
首先,需要對實際刮齒面與理論刮齒面進行假設,設實際刮齒面為 r∑(r∑,φ∑),理論刮齒面為 rLK(ρ,ξ,σk)。由于在刮齒過程中,待加工工件與刮齒刀對應的產形輪在節點處共軛,所以可以將工件節點作為依據來計算理論刮齒面的初始位置 σ0。
在車削內齒的過程中,工件與刀具的中心距為 a= rf1-rf2,rf1 為工件齒根圓半徑,rf2 為刮齒刀齒頂圓半徑。以漸開線為標準,根據刀具齒頂圓與工件齒根圓嚙合理論,可以推導得到:

式中:β1——工件的節距圓螺旋角;
r1———工件節距圓半徑;
p1———工件導程;
β01———工件分度圓螺旋角;
r01———工件分度圓半徑;
β2———產形輪節距圓螺旋角;
r2———產形輪節距圓半徑;
p2———產形輪導程;
β02———產形輪分度圓螺旋角;
r02———產形輪分度圓半徑。
考慮到車削外齒時,工件與刀具的中心距為 a=rf1+ rf2,以漸開線為標準,根據刀具齒頂圓與工件齒根圓嚙合理論,同樣可以用式(8)進行類似描述,但是需要對其進行修改,中心距為工件節距圓半徑與刮齒刀節距圓半徑之和,即 rf1+rf2=a。
無論是對直齒輪進行切削還是對斜齒輪進行切削,由于它們之間只是存在一個準角的關系,因此就刀具包絡齒輪理論而言,刮齒刀主刃都必須與齒輪齒面共軛的產形輪齒面對應。因此,主刀刃不僅位于產形輪齒面,更是前后刀面及產形輪齒面三者的交線,因此可以得到主刀刃參數方程:
式中:rr(r)——刮齒主刀刃上某一點在 S2 下的矢量;
r——刀具坐標系下,主刀刃上某一點到刮齒刀中心軸的距離。
根據式(8)和式(9)可以對主刀刃節點和工件節距圓半徑進行求解。
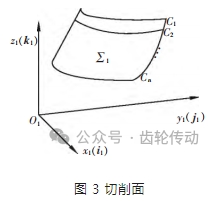
根據刮齒加工過程,若干次切削共同作用完成工件加工齒面。刮齒刀在每次切削進程中都會在 S1(O1- x1 y1 z1)下形成一個空間曲面∑1,如圖 3 所示。C1 表示 t1 時刻的切削刃,基于空間運動學原理,可得刀刃切削面方程:
式中:rx——切削面上某一點在 S1 下的矢量;
T——S2 到 S1 的總變換矩陣。
為方便描述,令:
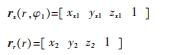
如圖 4 所示,根據刮齒坐標系可以對總變換矩陣 T 進行如下描述:
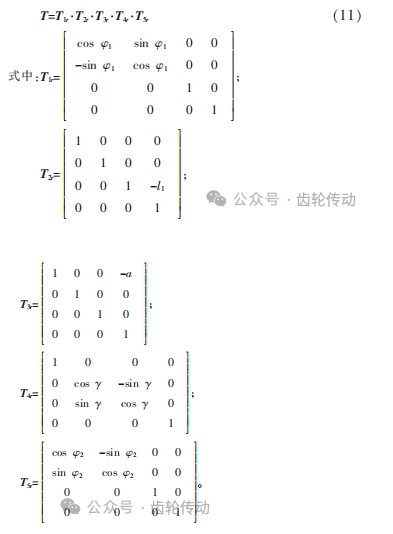
通過式(8)和式(9)可對刮齒刀主刀刃對應節點和工件節距圓半徑進行描述。同樣,通過式(10)和式(11)描述的坐標變換及 S1 坐標系上投影點與 x1 軸之間的夾角關系,可以對理論刮齒面的初始位置進行描述:
式中:σk——S1 坐標系上投影點與 x1 之間的夾角;
θk——節距圓處螺旋面轉角。
根據刀齒包絡理論中理論刮齒面初始位置最小原則描述初始區間長度 LDK:
式中:θa,θf——工件齒頂處與齒根處的螺旋面轉角。
由此可以推導兩個相鄰理論刮齒面的初始位置:

為提高計算效率,擬采用離散網格+跟蹤法對工件任一點與理論刮齒面之間的距離 lc 進行計算。根據求解出的初始點找出 lc。如圖 5 所示,假設任一點為 Q,對應理論刮齒面上的點為 p,點 p 在進行加工之前初始位置為 p0,Q 到 p 和 p0 的方向矢量定義為 U 和 S。由式(7)得到點 p0 在 S 和 U 兩個方向矢量上的偏導數 rLρ 和 rLξ。對矢量 S分別在U,rLρ 和 rLξ 三個方向上進行分解,可以描述為:
式中:d,AL,BL——矢量 S 在 U,rLρ,rLξ 三個方向上的投影系數。
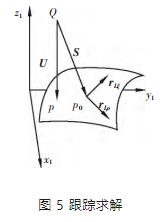
將 S 分別對 rLρ,rLξ 進行點乘求解,可以得到:

對式(16)進行求解,得:

將式(17)和式(18)作為依據,可以得到采用跟蹤求解理論刮齒面時需要的參數迭代量:
根據式(17)和式(19),采用跟蹤求解法求解 lc,令 n 表示迭代次數,可以得到:
三、參數優化及正交試驗
如文中描述,帶有增量的刮齒進給運動對工件邊緣的實際刮齒與理論刮齒之間存在誤差。引起齒側和齒根偏差的進給深度與不同的刀具參數、加工參數有關,例如齒輪和刀具的齒比及軸向進給速度,如表 1 所示。利用提出的數學模型對加工精度進行精確評估和計算。
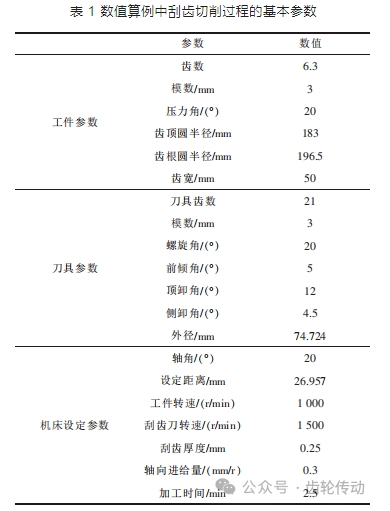
齒比與加工導程偏差
為了對齒輪齒數有關的齒廓偏差進行研究,將工件齒數分為奇數與偶數,并將齒輪和刀具的齒比納入討論范圍。與齒數和齒比相關的導程偏差如表 2 和圖 6 所示,假設工件齒數為 zg,當刮齒刀齒數為工件齒數的 2/3 時,當工件齒數為奇數時,刮齒刀每兩個齒輪旋轉 3s 就會切割出相同的間隙。而當工件齒數為偶數時,假設工件齒數為 zg,采用半齒數的刮齒刀,這就意味著每個齒輪旋轉 1s 就會切割出相同的間隙。
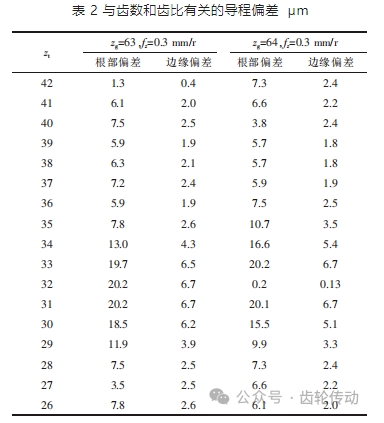
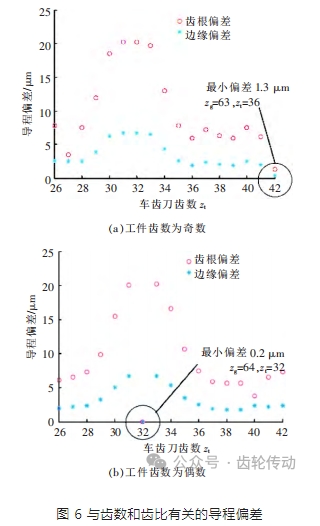
此外,如果刮齒刀齒數約為工件齒數的一半,除去齒數均勻,齒比恰好為 1/2 的情況,導程偏差大于其他情況。當工件齒數為奇數時,如圖 6a 所示,刮齒刀齒數 為 30,31,32,33 時,導程偏差最大,達到了 20.2 μm。
當工件齒數為偶數時,如圖 6b 所示,刮齒刀齒數為 31 和 33 時,導程偏差達到了 20.2 μm。由于工件和刮齒刀的齒比決定了齒側的導程偏差。因此選擇合適的刮齒刀齒數有利于提高刮齒加工精度。此外,若工件齒側質量要求較高,刮齒刀齒數應該利用最大公約數來選擇。但是需要避免使用半齒數的刮齒刀具,除非工件齒數為偶數,齒比恰好為 1/2。
軸向進給與加工導程偏差
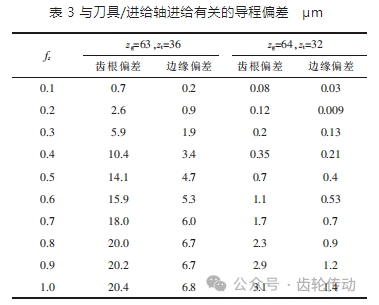
適當減少每個齒輪的軸向進給可以進一步減少進給誤差的深度。與刮齒刀軸向進給相關的導程偏差如表 3 和圖 7 所示。隨著軸向進給量的增加,導程偏差會逐步增大。例如當 fz=0.5 mm/r,zg=63,zt=36 時,工件齒輪導程偏差為 0.7 μm。然而當 fz=0.5 mm/r,zg=64,zt=32 時,工件齒輪導程偏差為 0.7 μm。因此,齒側進給量偏差與齒比有關。對于具有最大公約數的工件和刮齒刀的齒數,為了提高加工效率,需要提高軸向進給量。如果工件齒數與刮齒刀齒數不匹配,則必須選擇軸向進給,直至導程偏差滿足加工要求。然而,如果軸向進給量過小,導致刮齒刀運動與切削方向相反,則會增加刮齒循環時間。
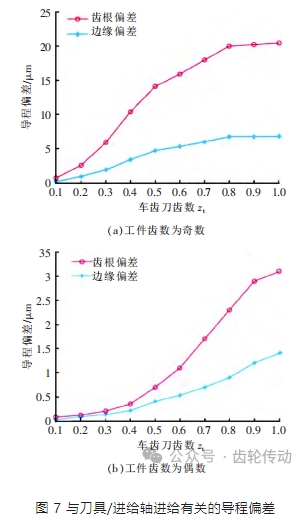
四、結論
通過對刮齒刀工作原理的分析建立了關于刮齒刀理論刮齒模型及實際刮齒與理論刮齒之間的偏差模型,對刮齒相關參數進行了研究,得出以下結論:
(1)隨著軸角和刀具直徑增大,頂前角減小。通過設置較大的軸角,選擇較大的刮齒刀直徑,可以獲得更好的切削角。
(2)工件齒數和刮齒刀齒數的齒比決定了齒側的導程偏差。對于邊緣質量要求較高的齒輪,刮齒刀齒數應該根據最大公約數來確定。并且除了齒數均勻,齒比恰好為 1/2 時,需要避免使用半齒數的刮齒刀。
(3)減少刮齒刀軸向進給可以進一步較少進給誤差。對于具有最大公約數的工件和刮齒刀的齒數,為了提高加工效率,需要提高軸向進給量。如果工件齒數與刮齒刀齒數不匹配,則必須選擇軸向進給,直至導程偏差滿足加工要求。
參考文獻略.
