齒輪的夾緊方式一般有徑向夾緊和軸向夾緊兩種,在夾緊齒輪后進行磨齒加工時,受到夾緊力場和磨削力場的耦合作用,導致相對于初始的安裝位置會有偏心和偏擺誤差,即位姿誤差,而機床上的砂輪并不會隨著齒輪位置的改變而進行補償修正,從而導致齒輪的加工精度受到影響。姜忠立等通過有限元法計算得到了齒輪加工中的變形量,并根據約束條件設計出合適的齒輪專用夾具。王歡以薄壁齒圈為研究對象,分析了夾緊力和切削參數之間的關系,以夾緊變形最小為目標優化,得到了扇形卡盤的扇形圓心角。鞏赟針對齒輪的液壓膨脹式精密夾具進行了有限元分析,計算得到了加壓后薄壁套筒的最大變形和夾緊力。段榮鑫通過有限元仿真分析了薄壁齒輪的夾緊變形規律,并用遺傳算法對夾緊力進行了優化。液壓膨脹芯軸是一種高精度夾具,能使加工后齒輪的徑向跳動≤3 μm。航空齒輪加工精度高,精度等級需達到5級以內,成形磨削作為齒輪精加工的最后一道工序,夾緊變形誤差和熱變形誤差能占到總誤差的40%~70%,因此有必要深入分析夾緊變形對齒廓偏差、齒距偏差的影響規律,以實現磨削參數的優選,這對提高齒輪成形磨削精度具有重要意義。
一、齒輪齒廓總偏差和齒距偏差的評定方法
在齒輪磨齒加工過程中,受諸多因素的影響,實際得到的齒輪齒廓總是會與理想的漸開線齒廓有一定的偏差,這些齒廓偏差的存在會導致齒輪傳動過程中不能保持恒定的傳動比,產生振動和噪聲,因此在GB/T 10095.1—2008的標準中對齒輪精度評級采用的是齒廓總偏差。因為實際加工得到的齒輪齒廓并不完全是漸開線,在漸開線與齒根圓連接處還有一段圓弧進行過渡,所以在計算齒廓總偏差前還要對計值范圍進行界定。GB/T 10095.1—2008中規定了從齒頂圓開始到齒廓上漸開線的起始點為齒廓的有效長度LAE,齒廓的計值范圍Lα為有效長度LAE的 92%。實際加工得到的齒輪齒廓示意圖如圖1所示,坐標系中的第一象限內有一條實際的右齒廓,假設已得到該齒廓上一系列測量點的坐標值(xi ,yi ),對于上面任一測量點K作過它的一條理想漸開線(圖中的細實線),設齒廓漸開線的基圓半徑為rb、K點坐標值為(xk,yk ),則漸開線上K點的向徑![]() 壓力角αk =arccos(rb/rk )、展角θk=tan αk-αk,K點向徑與X軸正方向的夾角φk為
壓力角αk =arccos(rb/rk )、展角θk=tan αk-αk,K點向徑與X軸正方向的夾角φk為
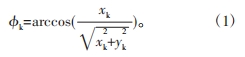
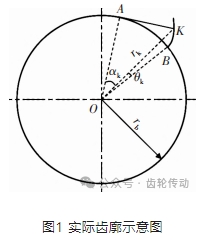
若K點在第三或第四象限,即yk ≤0時,需使φk=2π- φk。得到K點的展角θk及向徑與X軸的夾角φk后,則過 K點的理想漸開線起始角τk=φk-θk。
首先通過計算得到各測量點上的理論漸開線起始角τi,并從一系列τi 中找出τmin和τmax。根據漸開線的形成原理可知,同一基圓上兩個漸開線的法向距離等于基圓上兩漸開線起始點的距離,則實際齒廓的齒廓總偏差Fα為
當實際齒廓中同時有處于第一和第四象限的測量點時,得到的τmin和τmax會相差過大,此時求得的齒廓總偏差Fα是錯誤的,需要對其中一些測量點的τi 值進行修正。當τmax-τmin>2π/z時,從一系列測量點中找出τi >π的值進行修正,使τi =τi -2π,修正后再從一系列τi 中找到τmin和τmax,即可得到最終的齒廓總偏差。
齒輪齒距偏差的存在會使齒輪在傳動中產生振動、沖擊和噪聲,影響了齒輪傳動的平穩性,因此在齒輪的精度等級評定時還需考慮齒距偏差的大小,GB/T 10095.1—2008中的齒距偏差有3種,分別為單個齒距偏差、齒距累積偏差和齒距累積總偏差。齒距偏差示意圖如圖2所示,圖中實線為實際齒廓,虛線為理想齒廓,pt 為單個理論齒距pt =πd/z。單個齒距偏差fpt為在齒輪的分度圓上任意兩個相鄰同側齒廓的實際齒距與理論齒距之差。齒距累積偏差Fpk為任意 k+1個同側齒廓的實際齒距與理論齒距之差,理論上齒距累積偏差Fpk等于k個單個齒距偏差之和,k可從1取到齒數z。在任意齒距累積偏差中的最大齒距累積偏差為齒距累積總偏差Fp。
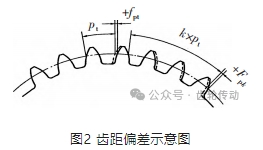
當齒廓在分度圓上的點坐標值(xi ,yi )已知時,利用余弦定理可以算出分度圓上相鄰齒廓兩點之間的向徑夾角θi,則單個齒距偏差fpti 可表示為:
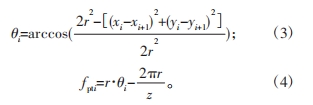
齒距累積偏差Fpk可表示為
通過計算得到一系列的齒距累積偏差最大值和最小值后,可求得齒距累積總偏差Fp為
二、成形磨齒齒面參數模型的建立
齒輪夾緊變形示意圖如圖3所示,若在齒輪初始安裝位置的中心上建立靜坐標系O0-x0y0z0,在齒輪夾緊變形后的位置中心上建立工件坐標系Oi -xi yi zi ,則可用齊次坐標變換矩陣表示齒輪位姿。
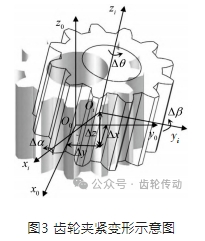
當工件坐標系Oi -xi yi zi 變換到靜坐標系O0-x0y0z0時,需要繞xi 軸轉動Δα,繞yi 軸轉動Δβ,再繞zi 軸轉動Δθ,最后再分別沿xi、yi、zi 軸平移Δx、Δy、Δz,由于轉動角 Δα、Δβ、Δθ都為極小的值,旋轉矩陣的次序沒有影響,設c代表cos、s代表sin,則齊次位姿變換矩陣為
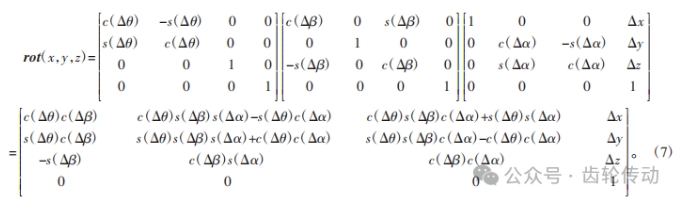
因為轉動角Δα、Δβ、Δθ都為極小值,所以各轉動角的cos()值為1,各轉動角的sin()值為其轉動角的弧度值,忽略變換矩陣中各項的高階無窮小,則矩陣可簡化為

忽略夾緊變形時,砂輪磨齒加工得到的齒廓在靜坐標系和工件坐標系下的參數方程均為標準漸開線參數方程,砂輪加工在靜坐標系的位置并不會改變。但是齒輪夾緊變形以后,砂輪在工件坐標系中的位置就會發生改變,利用靜坐標系與工件坐標系之間的齊次變換矩陣,可得到在夾緊變形條件下齒輪齒面方程為
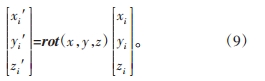
根據前述齒廓偏差和齒距偏差的評定方法,則可計算在夾緊變形條件下的齒廓偏差、齒距偏差。
三、齒廓總偏差和齒距偏差的計算步驟
齒廓總偏差的計算步驟如下:1)根據齒輪夾緊變形后的位姿變化,得到齊次坐標變換矩陣rot(x,y,z),將其與標準漸開線齒面方程相乘得夾緊變形條件下的誤差齒面參數方程;2)在第i個誤差齒面中部的齒廓上等間距取測量點,分別計算出各測量點的展角 θk、φk及τk;3)從各測量點的漸開線起始角τk中找出τmin 和τmax,根據式(2)計算出該齒廓的齒廓總偏差,若偏差過大,進行修正后重新計算;4)對各輪齒重復2)、3)步,求出各齒的齒廓偏差,各齒中最大的即為該齒輪夾緊變形條件下的齒廓總偏差。
齒距偏差的計算步驟如下:1)根據齒輪夾緊變形后的位姿變化,得到齊次坐標變換矩陣rot(x,y,z),與標準漸開線齒面方程相乘得夾緊變形條件下的誤差齒面參數方程;2)求出各個誤差齒面中部齒廓與分度圓的交點(xi,yi),根據式(3)、式(4)可算得各相鄰輪齒間的單個齒距偏差;3)根據式(5)、式(6)可算得齒距累積偏差和齒距累積總偏差。
四、位姿誤差對齒廓偏差、齒距偏差的影響規律
在夾緊變形條件下齒輪產生的位姿誤差可分為沿x/y軸的平移、繞x/y軸的轉動、沿z軸的平移和繞z軸的轉動4種,而沿z軸的平移誤差對齒輪的精度評定基本沒有影響,計算時忽略不計。以模數為4 mm、齒數為19、壓力角為25°、齒寬為72 mm的漸開線直齒圓柱齒輪為例,假設沿y軸平移的誤差Δy=3 μm、繞y軸的轉動誤差Δβ=0.02°,以及繞z軸轉動的誤差 Δθ=0.2°,并取齒輪中部橫截面的右側齒廓進行分析,分析各種誤差對齒輪齒廓偏差和齒距偏差的影響規律。
沿y軸平移3 μm誤差條件下得到的各輪齒的齒廓偏差、齒距偏差計算結果如圖4所示。由圖4可見,沿y軸的平移誤差對齒距累積偏差和齒距累積總偏差均會產生較大的影響,這兩項偏差的最大值大約是平移誤差的2倍(6 μm左右),而對齒廓總偏差影響稍小,產生的齒廓總偏差約為2 μm左右,對單個齒距偏差影響最小,產生的單個齒距偏差最大值約為1 μm,因此沿x/y軸的平移誤差主要會影響齒輪的齒廓總偏差和齒距累積偏差。
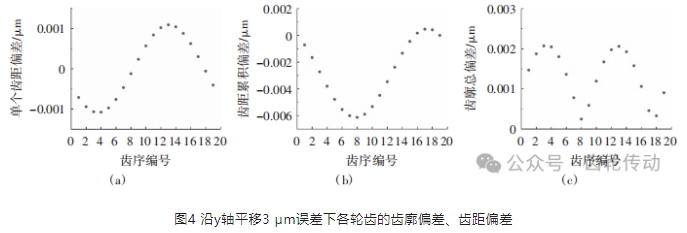
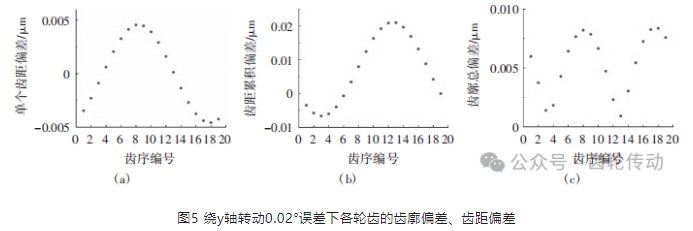
繞y軸轉動0.02°誤差條件下得到的各輪齒的齒廓偏差、齒距偏差計算結果如圖5所示。其中影響最大的是齒距累積偏差和齒距累積總偏差,偏差最大值分別約為22 μm和27 μm左右,其次是對齒廓總偏差的影響較大,產生的齒廓總偏差最大值約為8 μm,對單個齒距偏差的影響是最小的,產生的單個齒距偏差最大值在5 μm以下,因此沿x/y軸的轉動誤差主要影響齒輪的齒廓總偏差和齒距累積偏差。
當齒輪繞z軸轉動0.2°時,由于繞z軸的轉動誤差對齒距偏差基本沒有影響,僅考慮其對齒廓偏差的影響,經過計算發現齒輪上每個輪齒的齒廓總偏差大小基本相等,約為0.15 μm左右,這表明繞z軸的轉動誤差對齒廓總偏差的影響較小。
五、結論
本文綜合考慮夾緊變形的影響,通過齊次坐標變換矩陣建立了齒輪成形磨削齒面參數方程,分析了齒輪在夾緊變形條件下位姿誤差對齒廓偏差、齒距偏差的影響規律。結果表明:沿x/y軸的平移、繞x/y 軸的轉動這兩類位姿誤差主要影響的是齒輪的齒廓總偏差、齒距累積偏差及齒距累積總偏差,而對單個齒距偏差的影響較小。另外,繞z軸的轉動誤差對齒距偏差基本無影響,對齒廓總偏差影響較小。
參考文獻略.
