齒輪作為傳動系統的核心部件,被廣泛運用于航空航天、汽車坦克和高精密儀器制造等領域,噴丸強化是高性能齒輪制造的關鍵工序,通過齒根噴丸強化引入殘余壓應力可以有效提高齒輪使用壽命。噴丸與其他機械加工方法一樣,最終零件表面是凹凸不平的微觀形貌,這些微觀形貌的谷底區域在工件工作時會產生應力集中,表面粗糙度越大,產生的應力集中越嚴重,工件的疲勞壽命下降越快。因此,精確計算齒根噴丸粗糙表面的應力與應力集中系數對評估齒輪彎曲疲勞壽命極為關鍵。
對于粗糙表面與應力集中系數的關聯性研究,NEUBER將粗糙表面輪廓近似為連續相鄰的缺口, 并由缺口深度和寬度是影響缺口應力集中的主要因素,推廣到基于粗糙表面參數 Rz 和谷底曲率半徑 ρ 的應力集中系數計算公式。AROLA 等依據 NEUBER 提出的經驗公式建立了 Arola-Ramulu 模型,將實際的表面形貌近似為連續相鄰的正弦狀缺口展開研究,并通過實驗驗證了該模型的準確性。CHAN對電子束加工得到的板塊表面進行測量,研究了具有凹痕特征的形貌的應力集中,提出了加工制造過程中對表面形貌的要求;KANTZOS借助神經網絡,將應力集中和表面形貌進行關聯分析,實現了裂紋萌生的預測。在數值計算方面,學者們通過對具有特定規則的形貌進行簡化研究,采用一階邊界攝動法,基于 Hilbert 變換和能量守恒原理,預測了拉伸作用下二維表面形貌上的應力分布并進行實驗驗證。然而,目前可見文獻對于粗糙表面與應力集中系數的關聯規律大多基于二維表面形貌展開研究,對于三維實測表面形貌引起的應力集中研究較少,MEREUTA分別將 Neuber 模型和 Arola-Ramulu 模型的公式中二維粗糙表面參數轉換為對應的三維粗糙表面參數進行計算,并經過試驗驗證了修正公式的可靠性。LI基于表面形貌重構技術對重構表面引起的應力集中進行分析,利用少數幾個重構平面模型分析了粗糙表面參數 Sa 疲勞壽命之間的關系。XU研究了腐蝕對 Q235 鋼板疲勞壽命的影響,借助 ANSYS 軟件生成了三維粗糙形貌并分析了三種腐蝕坑與疲勞壽命的關系,最后與疲勞實驗進行對比驗證。在 GB/T 3480—1997 中通過大量的疲勞實驗提出了相對齒根表面狀況系數經驗公式,然而該經驗公式沒有給出粗糙度表面應力集中系數的計算表達式,而是通過相對齒根應力集中系數的比值擬合的公式間接獲得應力集中對齒輪彎曲疲勞壽命的影響,且該經驗公式僅用 1 個二維粗糙度參數 Rz 進行表征,顯然無法精確評估三維實際表面產生的應力集中。
隨著對三維表面的認識,用于表征粗糙表面形貌特征的三維粗糙度參數多達幾十個,不同的粗糙度參數表征表面的不同性能,而對于表征應力集中的三維粗糙度參數,目前尚未得到共識。且無論是二維還是三維粗糙表面問題,現階段所有研究對象均是以平板或者簡化為平面模型進行研究,解決齒根粗糙表面下實際應力精確計算,得到表征粗糙表面應力集中合適的形貌參數問題是高端齒輪、高性能齒輪設計制造的核心技術之一,具有較大的理論與工程應用價值。
論文以磨削后噴丸的直齒輪為研究對象,提取齒輪齒根三維粗糙表面形貌信息,依據空間坐標變換原理,研究齒根過渡曲面添加三維粗糙面的建模方法,從而突破現有齒輪強度分析只能創建光滑表面模型的限制,建立基于實測三維表面形貌的齒根區域有限元模型,對有限元計算得到的數據進行非線性曲線擬合,得到齒根三維粗糙表面參數與應力集中系數 Kt 的關聯公式,為后續的齒輪彎曲疲勞壽命精準預測和齒輪表面完整性參數設計提供相應的參考。
一、齒根表面形貌測量
為研究齒根噴丸表面危險區域的表面粗糙度與應力集中系數的關系,首先確定齒根危險區域的具體位置,基于磨削噴丸加工的齒輪(表 1),借助 Matlab 編程生成直齒輪齒廓,將齒廓導入 CATIA,通過陣列、拉伸等操作生成直齒輪實體模型,將齒輪實體模型導入 ABAQUS 中進行準靜態仿真分析,查看仿真結果應力云圖,確定了齒根危險區域(應力較大區域)。
其次,測量表面形貌。本文借助 ABAQUS 研究齒根危險區域表面粗糙度對應力集中的影響,通過調整網格節點坐標值實現粗糙度的添加,而齒根危險區域的網格數量取決于形貌測量的采樣點數,因此,選擇較為合適的采樣間隔減小網格數量、提高仿真效率是很有必要的。文中采用白光干涉儀 Wyko NT9100 對粗糙形貌進行測量。對于表面形貌的測量,采樣間隔越小,表面形貌還原越完整。考慮文中對有限元網格數量的要求,在保留形貌基本特征前提下,適當選擇較大的采樣間隔,舍棄部分形貌信息。一般地,采樣頻率大于形貌頻率 4 倍時,采樣離散數據點可以基本復原形貌的大致輪廓特征。
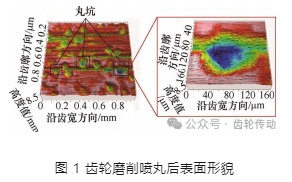
文中以噴丸后的粗糙表面為研究對象,主要研究噴丸處理后產生的丸坑形貌對應力集中的影響。一般地,表面形貌的應力集中最有可能產生在粗糙形貌最深的幾個谷底區域之一,已知齒輪噴丸直徑約為 120 μm,噴丸后產生的幾個最深丸坑深度平均值絕大部分在5 μm以上(詳細數據見表2中的 S10z ),則丸坑的表面直徑大于 40 μm。因此,在滿足采樣頻率大于 4 倍的形貌頻率(丸坑表面直徑)的基礎上,論文測量時選擇采樣間隔為 10 μm,采樣面積為1 mm ×1 mm。得到磨削后噴丸表面形貌如圖 1 所示。
二、考慮三維粗糙度的齒根應力有限元計算
齒輪網格劃分及細化
齒根應力有限元計算需要精確的齒根形貌與齒面形貌,漸開線齒面的計算按漸開線方程計算,齒根過渡曲面的構建按課題組前期提出的建模方法構建,詳細齒根過渡曲面構建方法可參考文獻。
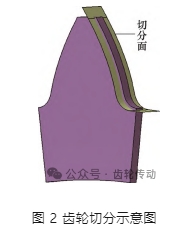
本文通過調整網格節點坐標實現粗糙度的添加工作,在齒根區域的網格節點數目應與采樣離散點的數目一致。考慮直齒輪實體模型是由齒廓方程生成的,沿齒廓方向各點的受力狀態基本相同。因此在建立齒輪有限元模型時將表 1 直齒輪參數的齒寬設定為與采樣面積寬度一致的 1 mm,大大降低重復的網格數量。此外,為了驗證齒寬為 1 mm 時齒輪有限元模型的可靠性,考慮模型邊緣效應等問題,分別對齒寬為 1 mm、5 mm、10 mm 的有限元模型進行仿真,保證其他邊界、材料等條件相同,載荷扭矩分別為T、5T 、10T 進行仿真,并對仿真結果進行對比分析,仿真結果表明三種齒寬條件下齒根彎曲應力的最大值相差在 5%以內,證實 1 mm 齒寬條件下齒輪模型的可靠性。其次將齒輪切分成兩部分,一部分包含齒根危險區域,需要進行網格細化,另一部分不需要調整網格節點,因此,網格數量不做要求。切分操作在 CATIA 中完成,具體切分過程如圖 2 所示。
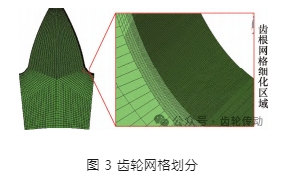
將切分后的齒輪兩部分分別導入 Hypermesh 中進行網格劃分。對齒根危險區域網格進行局部細化,齒根細化區域網格尺寸為10 μm ×10 μm,細化層數為六層。同時,為保證網格質量,在齒輪嚙合區域網格與齒根危險區域網格的尺寸相差不宜過大,未包含齒根危險區域部分齒輪對仿真過程關注的彎曲應力無影響,網格尺寸可盡量調大,最后劃分得到有限元網格數約為 25 萬,直齒輪的網格劃分模型如圖 3 所示。
齒根危險區域表面粗糙形貌的生成
將 Hypermesh 劃分好的齒輪模型保存為 inp 文件導入 ABAQUS 中,借助 Python 對 ABAQUS 進行二次開發實現齒根粗糙形貌的添加,具體操作步驟如下所示。
(1) 刪除直齒輪有限元模型中非齒根細化區域網格,保留齒根網格細化區域。
(2) 對齒根網格細化區域表層創建節點集,創建節點集后刪除表層網格選擇第二層網格表面創建節點集,依次創建不同層數的節點集,此處論文創建六層節點集。
(3) 利用 Python 對 ABAQUS 進行二次開發,提取步驟(2)中創建的節點集的節點坐標信息;
(4) 由步驟(3)獲得的節點坐標信息是雜亂無序的,對節點坐標依次按照節點沿齒廓方向以及節點高度值大小進行排序,獲得規則的網格節點編號以及對應節點坐標;
(5) 基于空間坐標變換原理,將采樣離散點高度信息以垂直于齒根危險區域曲面的方式分別對應添加到 ABAQUS 提取的節點集中,即改變相應節點的坐標值。具體變換過程如圖 4 所示。
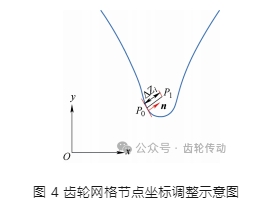
如圖 4 所示,直齒輪由齒廓曲線沿齒寬方向拉伸生成,因此用平面齒廓曲線代替直齒輪模型。其中,P0 為齒廓上齒根危險區域的一點,該點坐標由步驟(4)獲得,P0 點對應曲線上的法向量![]() 由齒廓方程得到,ΔZi 為采樣離散點高度值,P1 為 P0 沿其對應法向量 n 方向上添加形貌高度值 ΔZi 后的坐標。其中,第一層網格節點垂直曲面高度增加值為 ΔZi 的 6/6 ,第二層網格節點垂直曲面高度增加值為 ΔZi 的 5/6 ,第三層增加值為 4/6 ,依次類推,直至離散點高度信息全部添加完成。
由齒廓方程得到,ΔZi 為采樣離散點高度值,P1 為 P0 沿其對應法向量 n 方向上添加形貌高度值 ΔZi 后的坐標。其中,第一層網格節點垂直曲面高度增加值為 ΔZi 的 6/6 ,第二層網格節點垂直曲面高度增加值為 ΔZi 的 5/6 ,第三層增加值為 4/6 ,依次類推,直至離散點高度信息全部添加完成。
(6) 將修改完成的網格節點信息替換前面的齒輪模型 inp 文件對應的網格節點,至此,齒根危險區域表面粗糙形貌生成。
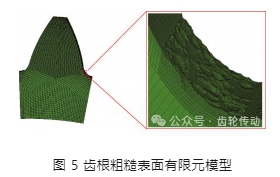
生成的齒輪形貌示意如圖 5 所示。
直齒輪的齒根應力仿真計算
為了獲得粗糙表面參數與應力集中系數的關聯規律,根據 ISO 25178 標準,選擇其中幾個常用的空間粗糙度表征參數進行計算分析:算術平均高度 Sa 、最大谷深 Sv 和十點區域高度 S10z 。各參數的定義如下
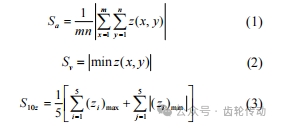
式中,z 為采集形貌離散點的高度,i和 j 分別表示噴丸形貌的凸峰和凹谷。三維粗糙表面參數 Sa 、Sv 、S10z 與之對應的二維粗糙表面參數為 Ra、Rv、Rz,二維粗糙表面參數是在三維粗糙表面上截取一條線段進行計算,因此,二維粗糙表面參數會丟失部分形貌信息,為了更完整地研究粗糙表面產生的應力集中,論文選擇三維粗糙表面參數進行形貌表征。
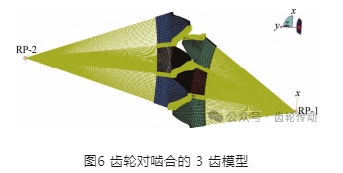
完成齒根危險區域添加表面粗糙度的工作后,論文選擇三組齒輪副的嚙合模型作為研究對象,其中小齒輪的中間齒輪為添加粗糙度的齒輪,兩邊齒輪則未添加。建立耦合和接觸對,將切分的包含粗糙度的中間齒輪用綁定約束進行連接,添加載荷并設置約束條件,采用準靜態分析方法進行仿真分析,齒輪對的有限元模型如圖 6 所示。
為了研究齒根危險區域表面粗糙度與應力集中系數的關聯規律,本文采用的應力集中系數定義如下
式中,σmax 表示帶有缺口模型的缺口處應力最大值,σn 表示光滑試樣無缺口的名義應力。此處取σmax 為添加粗糙度齒輪模型齒根彎曲應力最大值,σn 為無粗糙度時齒根彎曲應力最大值。由該定義可知,通過兩者的比值可消除 1 mm 齒寬與實際齒寬不同帶來的影響。
將添加粗糙度的齒輪仿真得到的齒根彎曲應力最大值與未添加粗糙度的齒輪彎曲應力最大值相比,即得到該粗糙表面參數下對應的應力集中系數 Kt 。有無粗糙度的齒輪彎曲應力分布對比如圖 7 所示。為了更清晰地看出齒根粗糙度表面的應力分布,只選取齒輪切分包含齒根危險區域部分的進行展示。
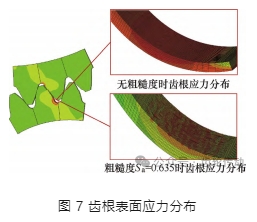
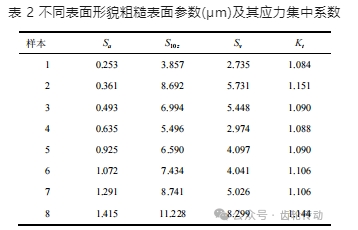
如圖 7 所示,帶有表面粗糙形貌的齒根應力分布與無粗糙度時的齒根應力分布相差較大,粗糙表面的齒根應力集中主要分布在表面形貌的波谷處,符合實際情況。取 8 個形貌樣本進行仿真分析,得到各粗糙表面參數與應力集中系數之間的仿真結果如表 2 所示。
三、粗糙表面參數與齒根應力集中系數關聯規律
不同于現有對平面粗糙形貌應力集中研究的計算方法,論文提出了一種考慮齒根過渡曲線宏觀幾何結構上的微觀形貌產生的應力集中求解方法。為了驗證論文所研究的求解方法,將論文的仿真結果與 GB/T 3480—1997 中的相對齒根表面狀況系數 YRrelT (通過試驗獲得)進行比較。
在 GB/T 3480—1997 中,齒根表面狀況系數的定義是“考慮齒輪根部的表面狀況,主要是齒根圓角(即齒根危險區域)處的表面粗糙度對齒根彎曲強度的影響”,齒根表面狀況系數即為齒根粗糙表面產生的應力集中系數。而相對齒根表面狀況系數定義是“所計算齒輪的齒根表面狀況系數與試驗齒輪的齒根表面狀況系數的比值”,給出的計算經驗公式是
式中,Rz 為二維粗糙表面參數中的微觀不平度十點高度,Rz 對應論文中的十點區域高度 S10z,基于 S10z 的相對齒根表面狀況系數公式為
論文仿真計算的表面粗糙度產生的應力集中系數(齒根表面狀況系數),與相對齒根表面狀況系數的定義不同,因此,不能直接將粗糙表面參數代入求解,需要進行轉換計算,轉換計算的原理方法如下:將國標中定義的試驗齒輪(粗糙表面參數 S10z =11.27 μm )對應的應力集中系數除以所需要計算齒輪的應力集中系數即為該計算齒輪的相對齒根表面狀況系數。試驗齒輪的粗糙表面參數 S10z 與樣本 8 基本相同。因此,應力集中系數按樣本 8 數據進行計算,經轉換計算,表 2 中各粗糙度對應的仿真計算獲得的相對齒根表面狀況系數為樣本 8 的應力集中系數除以對應樣本的應力集中系數。將各個樣本對應的十點區域高度 S10z 代入式(6)中,即得到國標經驗公式所計算的YRrelT 值。對比結果如圖 8 所示。
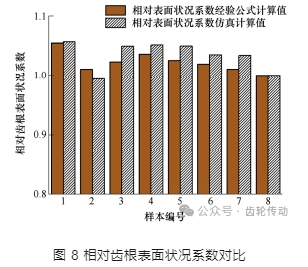
如圖 8 所示,仿真計算得到的相對齒根表面狀況系數與國標經驗公式計算得到的系數整體趨勢相同,且兩者計算得到的系數值也十分接近。此外,在國標中注釋了經過強化處理(如噴丸)的齒輪,其相對齒根表面狀況系數要稍微大于計算經驗公式所確定的數值,從圖 8 整體趨勢不難看出仿真值稍微大于經驗公式計算的數值,與國標中的注釋說法一致。圖 8 從側面論證了論文仿真求解方法的可信度。此外,國標經驗公式間接表示了齒輪齒根處形貌引起的應力集中,而本文則直接求解對應形貌的應力集中,表現更加直觀、具體。此外,與實驗獲得應力集中時耗時耗力相比,通過論文可以快速、低成本計算出應力集中系數,為后續精確計算齒輪彎曲疲勞壽命提供技術支持。
為了得到噴丸表面三維粗糙表面參數與應力集中系數的關聯規律,借助 Matlab 軟件的 cftool 工具包對表 2 中的數據進行關系式擬合,得到擬合關系如圖 9 所示。
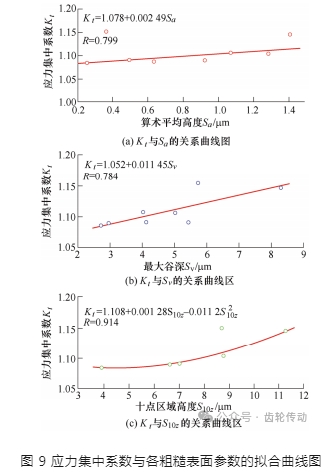
圖 9a、9b、9c 分別表示粗糙表面參數 Sa 、Sv 、S10z 與應力集中系數 Kt 的擬合曲線圖,對應的擬合相關系數 R 分別為 0.799,0.784,0.914。在對 Kt 的擬合關系中,十點區域高度 S10z 的擬合效果最好,擬合公式如式(7)所示
式(7)的擬合公式可以較好表征粗糙表面形貌與應力集中系數的定量關系。需要說明的是,加工零部件圖紙上標注的粗糙表面參數 Ra 是粗糙表面的二維表征參數,表征三維粗糙表面具有一定的局限性,選擇三維粗糙表面參數更為合適。從論文的分析結果看,為更加科學的表征三維粗糙表面對應力集中的影響,使用十點區域高度參數 S10z 更加科學,工程應用中,可優先使用 S10z 對應力集中系數進行計算。
四、結論
(1) 本文提出了一種基于齒根三維粗糙表面形貌的有限元建模與分析方法,解決了三維粗糙齒根表面應力集中系數計算問題,為齒輪表面完整性與抗疲勞設計研究提供了一種基礎方法。
(2) 論文采用有限元計算得到的表面粗糙度引起的應力集中系數與 GB/T 3480—1997 中給出的相對齒根表面狀況系數經驗公式進行間接對比,兩者計算結果基本相同。
(3) 對有限元計算得到的數據進行擬合分析,結果表明粗糙表面參數 Sa 、Sv 、S10z 擬合應力集中系數的擬合公式的相關系數分別為 0.799,0.784, 0.914,十點區域高度參數 S10z 能較好地表征齒根表面的應力集中,工程應用中可用十點區域高度 S10z 對噴丸粗糙表面產生的應力集中進行計算與表征。
參考文獻略.
