大規格漸開線圓柱齒輪在礦山、海洋、冶煉、能源等領域扮演著重要的角色,承擔著大功率、重載荷運動傳輸、能量傳遞等任務。齒廓偏差是衡量齒輪工作平穩性的重要指標。大規格齒輪制造工藝異常復雜,造價及其高昂。如何控制其加工工藝過程,保證成品率、提高加工質量,一直是亟待解決的問題。
傳統的齒廓偏差檢測方法主要是借助大規格坐標測量機或專用的CNC齒輪測量中心,如:Leitz公司的PMM-G、Zeiss公司的ACCURA系列、Gleason公司的GMS系列等。這種方法屬于離線測量,存在著兩個方面的缺陷。首先,離線測量法會不可避免地產生二次裝夾誤差,引起加工與測量基準的不重合,從而導致加工精度的流失;第二,被測齒輪需要在機床與測量設備上往返轉運,而大規格齒輪體積大、重量大的特點會造成安裝找正難度大、操作勞動強度大、工藝過程時效性差等問題。集成在機測量技術的出現妥善解決了上述問題,它將精密測量技術融入工件的制造工藝過程,在工件加工位置上檢測其加工誤差并進行補償,實現了“加工-測量”的閉環制造模式,有效提高了加工精度及生產效率,實現了工藝過程的自動化、智能化。近年來,在機測量技術得到了廣泛的應用,如齒輪、燃氣輪機轉子、大尺寸薄壁零件、渦輪、高精密非球面廓形等。
齒廓偏差的在機測量方法一直是各方的研究熱點。王燕玲等提出了一種采用齒條形刃邊測頭測量齒廓偏差的方法;段振云等提出了一種基于直母線族的齒輪在機測量方法。這兩種方法將測量儀器定位在機床或齒輪上來完成測量,測頭定位精度不高,測量精度較低。高峰等應用觸發式測頭在齒形磨齒機上實現了齒廓偏差的在機測 量;王志永等研究了螺旋錐齒輪齒形誤差的在機測量方法;喬衛東等研究了大齒輪齒形掃描式在機測量的數據處理方法;這些方法均依靠機床自身的運動及位置檢測功能實現測量,充分發揮了機床的伺服控制功能。然而,機床各伺服軸不可避免的存在著幾何及運動誤差,會導致測量誤差。上述研究并未給出合理的測量精度提升解決方案。為此,Hartig. F等應用激光跟蹤儀實現了大規格漸開線齒輪齒廓及螺旋線偏差的測量;石照耀等詳細研究了基于激光跟蹤技術的特大型齒輪的在位測量方法,給出了測量定位模型及姿態調整模型;陳洪芳等研究了面向特大型齒輪的激光跟蹤多站為定位方法;這種測量方法利用激光絕佳的測距及跟蹤功能替代了機床的位置測量系統,能夠更為精確地獲取齒面測點的位置信息,避免了機床幾何及運動誤差對測量結果的影響,擁有較高的測量精度。但是,激光光路易因遮擋而導致測量中斷,且其測距性能也易受溫度場變化而發生波動,導致測量精度降低。此外,激光跟蹤儀使用成本高昂、調試操作復雜,難以適應加工現場大規模應用的要求。綜上所述,探究一種充分發揮機床的運動及精度潛能、廣泛適合加工現場應用并具備誤差補償修正功能在機測量方法是十分必要的。
為此,本文提出了一種基于機床自身運動及位置檢測功能大規格漸開線齒廓偏差的集成在機測量及其誤差補償方法。建立了漸開線螺旋面綜合測量模型;確定了測量方案;推導了機床幾何及運動誤差與測量誤差之間的映射關系;計算了各測點對應的測量誤差;提出了測量誤差的后補償方法;最后,在一臺五軸數控成形砂輪磨齒機上進行了齒廓偏差的在機測量及其補償實驗。
一、在機測量方法
測量系統的組成
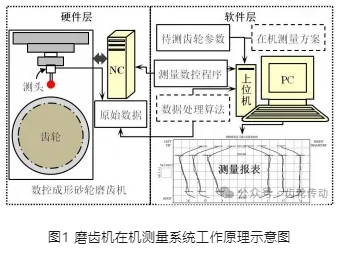
采用掃描測頭測量漸開線齒廓時,探針與被測齒面相接觸,數控系統控制測頭與齒輪以理論構型曲線為目標軌跡相對運動。若齒面存在加工誤差,則實際構型曲線與理論構型曲線編存在偏差,引起探針發生偏轉,上位機將所有的偏轉量記錄下來,再經過數據處理即可得到被測齒輪的齒廓偏差。在機測量系統的構成如圖1所示。
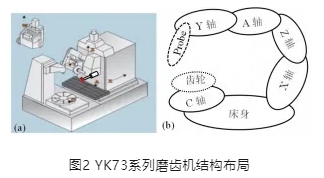
YK73系列數控成形砂輪磨齒機擁有六個伺服運動軸,如圖2(a)所示,分別為:立柱徑向進給軸X、縱向砂輪進給軸Z、齒輪分度軸C、螺旋角旋轉軸A、砂輪修形軸(齒輪切向)Y及砂輪修形軸(垂直方向)W。各伺服軸間的拓撲關系如圖2(b)所示,機床擁有“測頭-Y軸-A軸-Z軸-X軸-床身”及“床身-C軸-齒輪”兩個運動鏈。
測量方案的分析與確定
數控機床擁有的伺服軸數往往多于在機測量方案所需的伺服軸數,即一個在機測量方案會有多個在機測量運動控制方案。由于數控機床各伺服軸的的精度水平不盡相同,不同的測量方案會有測量精度的高低差異。確定合理的測量方案應遵循以下準則:
1)參與伺服軸最少原則
機床各伺服軸相互串聯,測頭的軌跡受各軸及軸間的各種形式的誤差疊加耦合影響,產生測量誤差。因此參與測量運動的伺服軸越少越好;
2)重心偏移最小原則
機床伺服軸重心的偏移會引起機床的變形,產生幾何及運動誤差,進而導致測量誤差。測量運動引起機床重心偏移最小的方案,為應優先選取的方案;
3)長度基準最短原則
由于長導軌制造精度較難保證,特別是在機床上,工況復雜,長導軌的精度流失更為嚴重。因此在確定測量方案時,應避免選取存在相對較長線性移動量的測量方案。
漸開線齒廓的測量方案
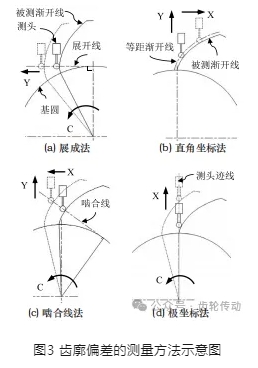
常見的漸開線齒廓測量方法,如圖3所示,包括直角坐標法、展成法(法向極坐標法)、嚙合線法、極坐標法等。
1)展成法(法向極坐標法)
幾乎所有齒輪量儀都采用該方法。測頭沿漸開線的展成方向運動。機床提供回轉運動及高精度直線運動。展成法需要高精度直線導軌作為測量基準。漸開線規格越大,所需的直線導軌越長。而高精、大規格的直導軌往往難以制造。并且,在機床的工況環境下,長導軌的實際使用精度的保證往往是一個難題。此外,在YK73系列數控成形砂輪磨齒機上,漸開線的展成方向為機床Y軸方向,而Y軸為砂輪修整成形軸,行程很短,無法滿足展成法的要求。因此展成法不適合作為在機測量方案。
2)直角坐標法
測頭由機床直線軸X軸及Y軸帶動,探針球心軌跡為被測漸開線的等距線。受機床結構影響,測頭的安裝位置距Y軸的中心(重心)位置存在偏置量,如圖2所示。為了使測頭在測量時正對被測齒槽,需要以抵償上述偏置。由于Y 軸行程很短,抵償偏置后往往已接近Y軸一端行程的極限位置,大大限制了測量運動范圍,難以滿足較大規格漸開線的測量。此外,Y軸上安裝有砂輪、電主軸及其附屬裝置,質量較大,重心的偏移會導致Y軸自身的直線度誤差及X、Y 軸間的垂直度誤差,引起機床的幾何及運動誤差,進而導致測量誤差。因此直角坐標法不是最優的在機測量方案。
3)嚙合線法
探針球心的運動軌跡為被測漸開線的嚙合線。這種方法雖有效避免了展成法中對于長導軌的要求,但是測量運動需要機床X、Y、C三個伺服軸插補完成。由于機床是由各運動軸串聯而成,每個軸及軸與軸之間的各種形式的誤差相互疊加最終作用在測頭的軌跡上,引起測量誤差。顯然,參與在機測量的伺服軸越多,測量誤差越大。
4)極坐標法
由機床回轉軸C軸及X軸做插補運動完成測量。其優勢在于測量過程中不存在機床的重心的偏移。同時,避免了對較長導軌幾何及運動精度的要求。綜上,本文選擇極坐標法進行漸開線齒廓偏差的在機測量。
測量模型的建立
測量過程中,探針始終與漸開線螺旋面相切,兩者的空間相互位置關系如圖4所示:在過測點k的漸開線螺旋面的法平面內,測球同法平面與螺旋面的交線相切于測點k;在齒廓偏差的測量平面(螺旋面任意端截面)內,測球與被測漸開線在k點相切。
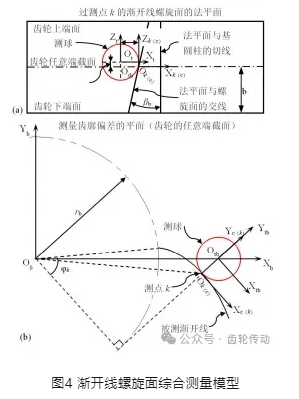
不妨建立如下坐標系:ΣOb齒廓偏差測量坐標系,固定在距齒輪下端面距離為b的端截面內,原點位于被測漸開線的基圓圓心;ΣOk為在端截面內通過測點k的漸開線法平面坐標系,其原點位于基圓與法平面的切點處;ΣOc為在探針測球球面上的觸點坐標系,測量過程中與ΣOk重合;ΣOt為測球球心坐標系;ΣOtb為齒廓偏差測量界面內測球的截面坐標系,各坐標軸方向與ΣOt相同;ΣOm為機床(齒輪)坐標系,設置在齒輪下端面,圓心位于齒輪的中心,其各坐標軸方向與機床各伺服軸方向相同。
根據圖4所示的各坐標系之間的相互位姿關系,應用齊次坐標變換原理,在ΣOm下描述測量過程中探針球心Ot的位置,即可得到漸開線螺旋面綜合測量模型:

式中,φk為被測點k對應的展開角,rb為被測齒輪的基圓半徑,r0為探針測球半徑,βb為被測齒輪基圓螺旋角。
在機測量時,齒輪在C軸帶動下做回轉運動,為保證測頭與齒輪的始終接觸,測頭由X軸帶動應做相應的直線移動,伺服軸間的關系為:
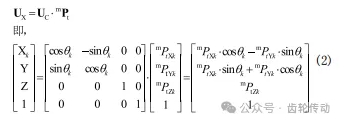
式中,θk、Xk、Y、Z分別為測點k對應的機床C軸、X 軸、Y軸、Z軸在機床坐標系下的坐標。
由于機床Y軸始終停在一個固定位置上,假設在機床坐標系下其坐標值為e,則有:
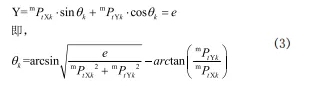
則各測點對應的機床X軸及C軸的在機床坐標系下的坐標:
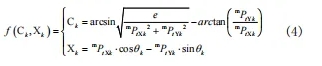
二、誤差補償方法
補償原理
數控機床的幾何及運動誤差會導致插補運動產生的實際理論構型曲線與標準理論構型曲線存在偏差,引起測頭探針的誤偏轉,產生測量誤差。通過建立機床空間綜合誤差與測量誤差之間的映射關系,計算出測點的誤差,進而對測量誤差進行補償,從而提高在機測量精度。齒廓偏差在機測量誤差補償方法的基本流程如圖5所示。
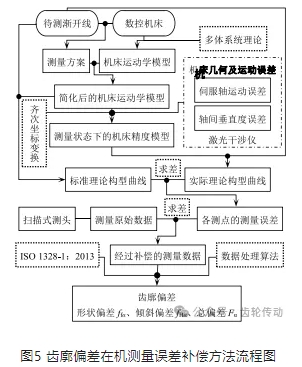
首先,根據測量方案對機床的運動構型進行簡化,應用多體系統理論建立對應于測量方案的機床運動學模型,并求出測量時的標準理論構型曲線坐標集;隨后,結合機床幾何及運動誤差,基于齊次坐標變換方法建立測量狀態下的機床精度模型,并求出空間誤差作用下的實際理論構型曲線坐標集;顯然,兩種構型曲線上各坐標點的差即為各測點的測量誤差;隨后,將掃描式測頭得到的測量原始數據與測量誤差求差,即可得到經過修正的測量數據;最后,依據ISO 1328-1:2013標準的規定,對測量數據進行處理,便可得到齒廓偏差的測量結果。
需要指出的是,數控機床空間綜合誤差的補償方法通常有兩種。一是前補償,即利用坐標點誤差修正原有NC程序刀具(測頭)點位,再進行加工或測量;二是后補償,即測量完成后,直接利用坐標點誤差修正測量原始數據。前補償大多應用于數控加工過程,其問題在于:修正后的 NC程序依然由包含誤差的伺服機構執行,補償精度是有限的。而后補償方法有效避免了前補償法中的二次補償誤差,更適用于在機測量誤差的補償與修正。
磨齒機精度建模
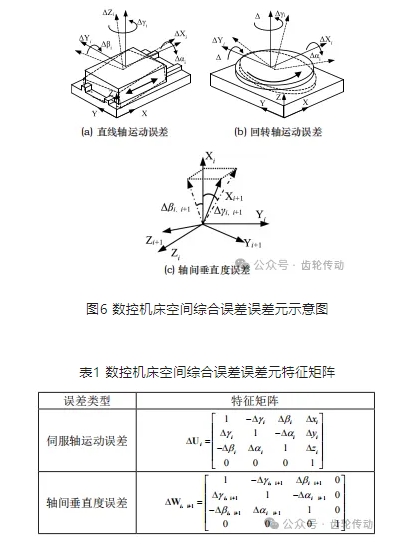
數控機床的空間綜合誤差由伺服軸的運動誤差及伺服軸間的垂直度誤差兩部分構成,如圖6所示。在三維笛卡爾坐標系內,伺服軸的運動誤差有六個自由度,包括沿三個坐標軸的平移及繞三個坐標軸的回轉。伺服軸間的垂直度誤差為繞三個坐標軸旋轉的角度誤差。兩者的特征矩陣如表1所示,矩陣中的各項元素的值均可通過激光干涉儀測得。
不妨將伺服軸的運動誤差及軸間垂直度誤差看作為機床各伺服軸的微小的錯誤運動。因此,采用齊次坐標變換的方法,按照機床的拓撲結構,將各誤差特征矩陣連乘起來便可得到機床(某側運動鏈)的空間精度模型:
式中,Δi+1Wi為伺服軸間垂直度誤差,Ui為伺服軸運動功能矩陣,ΔUi 為伺服軸的運動誤差。
測量誤差的計算
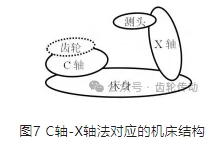
采用極坐標法,即C軸、X軸插補法測量漸開線齒廓時,YK73系列成形砂輪磨齒機的運動構型可簡化為如圖7所示的形式。
根據式(5)及式(2),測量狀態下機床的精度模型為:
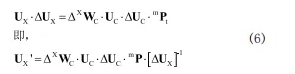
結合式(4)及式(6),可得到在機床幾何及運動誤差作用下,各測點對應的機床X軸及C軸的在機床坐標系下的坐標f'(Ck',Xk')。
那么,各測點的測量誤差為:
三、實驗
在一臺五軸數控成形砂輪磨齒機上進行了大規格漸開線齒廓的在機測量及誤差補償實驗,如圖8所示。被測齒輪主要參數如表2所示。

將齒輪參數代入式(1)及式(4)計算得到機床坐標系下各測點對應C軸及X軸的絕對坐標,據此編寫測量數控程序,完成測量。應用激光干涉儀分別測量機床C軸、X軸整個行程范圍內的各項誤差及兩軸間的垂直度誤差;結合式 (7)計算各測點的測量誤差,隨后對測頭記錄的原始數據進行修正、補償;最后依據ISO 1328-1:2013的規定計算漸開線齒廓偏差的各項評價指標。
首先,為驗證本文的測量方法及補償方法的有效性。隨機在齒輪上選擇一牙,以其右齒面為例,將其測量結果與齒輪量儀的測量結果進行對比,同時對比補償前后的結果。表3為齒廓偏差評價參數的對比結果。圖9為補償前后齒廓偏差測量曲線及與齒輪量儀計量結果的對比。
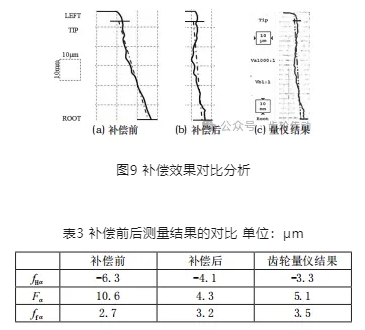
可以看出,本文提出的測量方法是可行的、有效的。通過補償,測量精度得到了明顯提高,補償后齒廓偏差的三項評價指標均接近齒輪量儀的測量結果。
在齒輪上選擇均勻分布的三個輪齒進行測量及補償實驗,驗證本文方法的可靠性及適應性。實驗獨立重復進行5 次。限于篇幅這里只將1號齒的測量結果展示在表4之中。
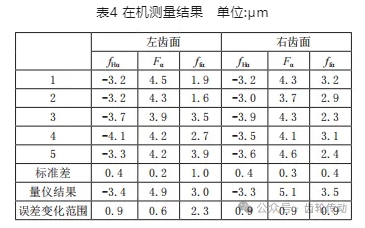
由表可知,各評價指標的標準差最小為0.2μm,最大為1μm,這說明測量結果的重復性較好,測量方法的可靠性較高。與量儀相比,除左齒面形狀偏差ffα外,5次測量得到的各評價參數誤差波動范圍均小于1μm,最小僅為 0.6μm,這驗證了測量方法的精確性。
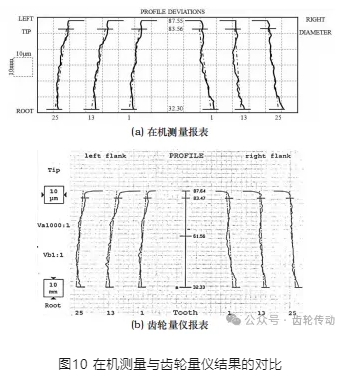
在5次測量結果中隨機選取某次的測量報表如圖10所示。可以看出,采用本文方法得到的齒廓偏差測量結果,在偏差大小、偏差位置、偏差形狀方面都與齒輪量儀的計量結果保持了較高的一致性。
四、結語
提出了確定合理的數控機床在機測量方案應遵循的準則;
針對大規格磨齒機結構特點,對比分析了各種漸開線齒廓測量方法的優劣,確定了極坐標法為最優的在機測量方案;
以探針與齒面嚙合關系為約束,推導了漸開線螺旋面綜合測量模型,建立了漸開線被測構型與機床伺服軸運動量之間的映射關系;
基于多提系統理論及齊次坐標變換方法,建立了對應于測量方案的機床綜合精度模型,推導了機床空間綜合誤差與測量誤差之間的函數關系;計算了各測點處的測量誤差,實現了在機測量誤差的后補償;
在一臺五軸數控成形砂輪磨齒機上進行了大規格漸開線齒廓的在機測量及誤差補償實驗,實驗結果證明了本文提出的方法有效、可靠、精度高。
參考文獻略.
