磨削加工是齒輪加工的最后一道工序,對齒輪產品表面粗糙度的影響最為關鍵。研究發現齒輪表面粗糙度會影響齒輪的工作壽命和使用性能,表面粗糙度越大,在嚙合過程中產生的摩擦力越大,容易產生微點蝕。在低速重載工況下,齒輪表面粗糙度越小,磨損越輕微; 在純電動減速器中,齒輪表面粗糙度降低,噪聲減少,齒面磨損速度減慢,從而提高齒輪壽命。
表面粗糙度是機械加工中描述表面微觀形貌重要參數之一,它主要反映機械零件表面的微觀幾何形狀誤差。國標 GB /T 3505 - 1983 包含了輪廓算術平均偏差 Ra 在內的多個表面粗糙度參數,在機械制造行業中使用最為廣泛。日本機械學會對齒輪傳動失效實例進行的系統調查結果表明,約 74% 的齒輪傳動失效是由于齒輪表面疲勞失效引起的,與齒輪嚙合時的齒面粗糙度有直接關系。齒輪在實際服役過程中,通常處于高速、重載和沖擊等工作環境,在交變載荷作用下,齒輪表面會在微觀凸峰部位產生應力集中,引發材料表面微裂紋的擴展,最終導致齒面的接觸疲勞,還會對齒輪的噪聲和振動特性產生不利影響。
筆者以 17CrNiMo6 - 4 鋼齒輪的蝸桿磨齒加工過程為研究對象,研究蝸桿砂輪加工參數對齒面粗糙度的影響。在此基礎上建立了多目標優化模型,并采用多目標非支配遺傳算法進行加工參數的優化求解。
一、實驗研究
實驗設計
實驗材料為 17CrNiMo6 - 4,材料性能如表 1 所示。磨齒實驗機床為德國 KAPP 公司的 KAPP - KX300p 數控磨齒機,采用德國馬爾 xcr20 粗糙度儀測量齒面粗糙度。實驗所用的蝸桿砂輪的參數與工件齒輪的參數如表 2 和表 3 所示。
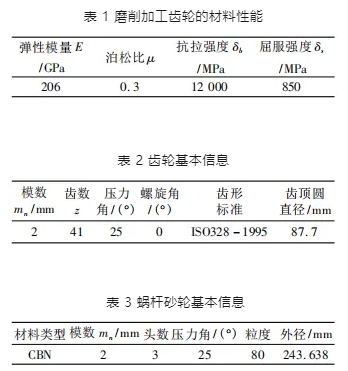
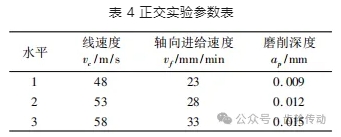
實驗零件磨齒前表面硬度為 59 ~ 62 HRC,硬化層厚度為 0.9 ~ 1.2 mm。最后一次加工直接決定零件的表面最終粗糙度質量,因此實驗以最后一次精磨加工過程為研究對象。本次實驗設計了砂輪線速度、砂輪軸向進給速度和砂輪單邊磨削深度 3 個影響因素的 3 水平 9 次正交試驗方案,參數水平是依據車間師傅的生產經驗以及設備參數要求設置,實驗參數如表 4 所示。
數據采集
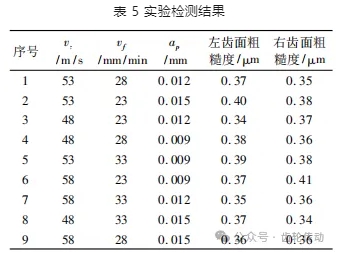
采用國馬爾 Xcr20 粗糙度儀測量齒面粗糙度,檢測結果如表 5 所示。為了觀測齒面兩側加工質量是否存在差異,分別統計左右兩齒面的表面粗糙度。
二、數據分析
對獲得的數據進行極差分析,表 6 為極差分析結果,Ti 為各因素在 i 水平表面粗糙度的總和, ![]() 為各因素在 i 水平表面粗糙度的平均值,極差為
為各因素在 i 水平表面粗糙度的平均值,極差為![]() 。
。
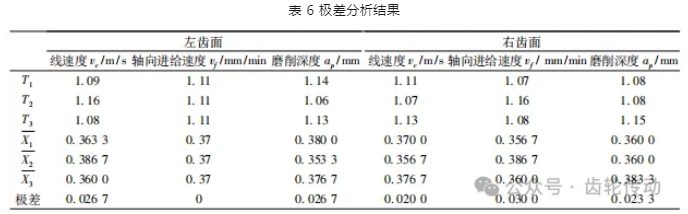
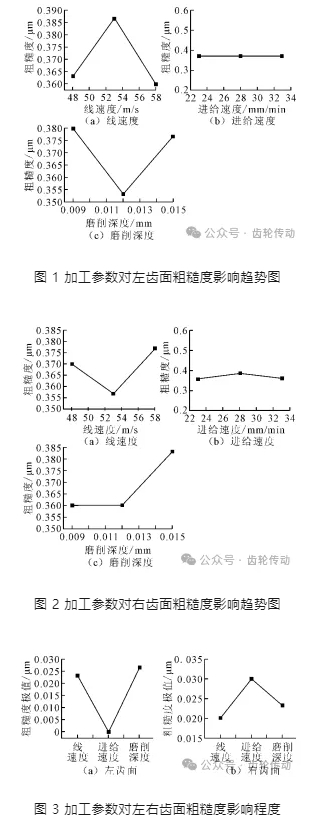
分析 3 個加工參數對左右齒面粗糙度的影響關系。圖1為左齒面分析結果,可以發現對于左齒面而言,在實驗砂輪軸向進給速度設定值內,隨著砂輪線速度增加,齒面粗糙度值先增大后減小; 隨著軸向進給速度的增大,齒面的粗糙度值沒有變化; 隨著磨削深度的增加,齒面粗糙度值先減小后增大。對于右齒面,在實驗參數設置范圍內,隨著線速度增加,粗糙度先減小后增大; 隨著軸向進給速度增大,粗糙度先增加后減小,但是變化值很小,幾乎沒有變化; 磨削深度增加,粗糙度后續逐漸增加,如圖 2 所示。實驗結果顯示出 3 個影響因素對左右齒面粗糙度值有不一樣的影響趨勢,如圖 3 所示,對左齒面粗糙度的影響因素由強到弱的是磨削深度、線速度、進給速度; 對右齒面粗糙度影響從大到小的是進給速度、磨削深度、線速。進給速度對于左右齒面而言,隨著進給速度的增加,粗糙度值的變化都很小,說明進給速度對齒面粗糙度的影響不大。
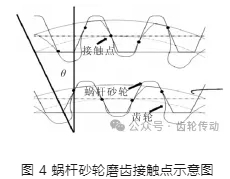
對于左右齒面影響規律不一樣的現象,郭寶安等分析磨齒加工過程,發現當齒輪旋轉一定角度后,齒輪與蝸桿砂輪的接觸面數量發生周期性變化。表明齒輪左右齒面受力不一致,齒輪加工過程中的形變不一致,從而導致左右齒面的齒面粗糙度受加工的影響規律不一樣。蝸桿砂輪加工齒輪時,齒輪與蝸桿的傳動可以近似為齒輪與齒條的傳動,因此可以近似認為齒輪是由齒條刀具加工而成。通過軟件 Gear TraxPRO2016 模擬齒輪與齒條的傳動過程,可以發現齒面的接觸點數量呈現周期性變化,如圖 4 所示。當嚙合轉動一個 θ 角度后,接觸點數從 5 個變成了 4 個,再轉過一定角度后又有 5 個接觸點,如此循環。
通過上面分析可知,在蝸桿砂輪磨齒加工過程中,加工參數對齒面粗糙度的影響不是簡單的線性關系,而是各加工參數之間的綜合影響結果。為進一步分析各加工參數對粗糙度的影響關系,采用二級逐步回歸方法進行線性回歸擬合。二級逐步回歸能根據各因素對響應變量的影響大小而自主取舍變量,能較好擬合關系不明確的模型。將左右齒面數據擬合,得到粗糙度回歸模型如式 (1) 和式(2) 所示。
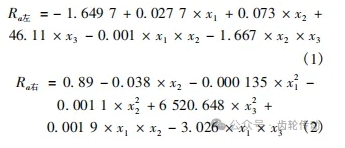
式中: x1、x2、x3 分別為砂輪線速度、砂輪軸向進給速度和砂輪單側磨削深度。
表 7 為左齒面粗糙度回歸模型顯著性檢驗結果,其中決定系數 R2 = 0.905,P 值為 0.091 4 > 0.05,表明對于左齒面而言模型的顯著性較差。

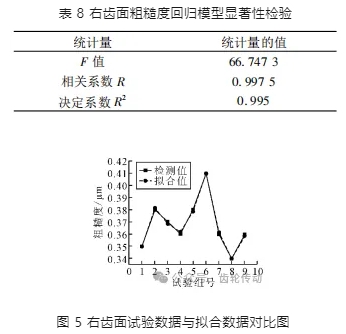
表 8 為右齒面粗糙度回歸模型顯著性檢驗結果,其中決定系數 R2 = 0.995,P 值為 0.014 8 < 0.05,表明在 95% 的置信度下,回歸模型具有較高的顯著性,可信度高。對比右齒面粗糙度擬合值和檢測值,如圖 5 所示。從圖 5 可知,右齒面粗糙度的模型擬合效果很好,可以準確地利用加工參數計算出粗糙度值。
對比左右粗糙度模型的擬合效果,右齒面模型顯著度更高,可以推測在本案例中加工參數對右齒面的影響更為規律和顯著,砂輪和齒輪之間的接觸狀態更加穩定。
三、磨齒加工參數優化
在實際生產過程中往往需要考慮多種條件下獲得綜合優化生產方案。磨齒加工過程中需要同時考慮加工效率和加工質量,因此將為獲得加工效率和表面粗糙度綜合優化加工參數展開研究。
優化目標
(1) 加工時間。減少加工時間是增加經濟效益的重要手段。在加工過程中,一個零件的加工時間包括機加工時間、安卸時間、系統輔助時間以及工人休息時間。對于一件產品而言,除了機加工時間,其他時間相對固定,因此減少加工時間是提高生產效率的主要方式。蝸桿砂輪磨齒加工時間計算公式為:
式中: B 為砂輪運行距離,包括齒面寬和安全距離,這里等于 42.5 mm; vf 為砂輪沿齒輪軸向進給速度。
(2) 表面粗糙度。降低表面粗糙度是生產加工過程中另一目標。由于加工參數對齒面粗糙度的影響關系不一致,因此需要同時考慮左右齒面的粗糙度。雖然左齒面的模型顯著性較差,但是右齒面的顯著性很好,因此同時考慮左右齒面能更符合實際生產情況,表面粗糙度的回歸模型為:
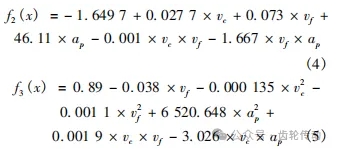
設計變量及約束
(1) 粗糙度約束。左右齒面都需要滿足最大加工粗糙度值約束。

(2) 表面燒傷約束。齒面燒傷會影響齒面性能,因此必須保證加工過程中齒輪不被燒傷。根據小野浩二公式,需要滿足:
式中: vc 為砂輪線速度; ap 為磨削深度; da0為砂輪直徑; Cb 為材料燒傷臨界值,不同的加工環境取不同的值。
在企業實際加工過程中發現當 Cb 值為 7 226 時發生輕微燒傷(線速度為 63 m /s,磨削深度為 0.015 mm) ,因此將此值作為臨界值。即
根據設備說明書及砂輪規格,以及設備老化的緣故,確定精加工階段加工參數的取值范圍。
(3) 砂輪線速度約束為:
48 ≤ vc ≤ 58 (10)
(4) 軸向進給速度約束為:
23 ≤ vf ≤ 33 (11)
(5) 切深的取值范圍約束為:
0.009 ≤ ap ≤ 0. 015 (12)
根據優化目標和約束條件得到優化模型:
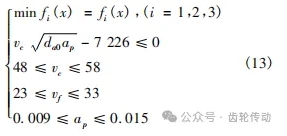
優化算法的選擇
本文研究的多目標優化問題、需要同時考慮多個可能擁有不同量綱、不同維度的目標函數,但是多個目標之間往往會相互制約,因此很難準確找出一個最優解,而是存在一系列不同的解,但是在這些解中,一定會至少存在一個解能使目標優于其它解,這樣的解稱之為非支配解,這些解的集合即為 Pareto 最優解集,Pareto 解集是被公認的多目標優化問題解的定義和表現形式。
筆者采用基于 Pareto 支配關系的多目標非支配遺傳算法 NSGA - II( non- dominated sorting genetic algorithm II) 對蝸桿砂輪磨齒加工參數進行優化。NSGA - II 算法是由 Deb 等提出的,主要從提高非支配排序效率、利用擁擠度距離代替共享參數、引入精英保留策略等方面對非支配排序遺傳算法 ( nondominated sorting genetic algo-rithm,NSGA) 進行了改進。NSGA - II 算法主要包括選擇、交叉、變異等算子,選擇機制主要是基于非支配排序和擁擠度距離來實現。在求解多目標優化問題中,NSGA - II 是目前應用最為廣泛的多目標優化算法。
NSGA - II 算法的邏輯流程如下:
(1) 初始化種群。在自變量上下限搜索范圍內,隨機生成初始種群,并且驗證計算每一組變量都滿足方程約束。接著計算每組變量所對應的目標函數值,然后對獲得的初始種群進行非支配排序,計算種群中每個個體的非支配排序等級和擁擠度距離;
(2) 種群繁殖。對父代種群按一定的比例進行選擇、復制后,進行個體之間交叉操作或個體的變異操作,從而生成子代種群;
(3) 非支配排序。把父代種群和子代種群進行合并得到中間種群,并對其進行非支配排序;
(4) 選擇生成父代種群。根據非支配排序等級和擁擠度距離結果進行選擇,在非支配排序后的中間種群中,篩選與初始種群規模相同的個體生成下次迭代的父代種群;
(5) 判斷終止條件。根據終止規則,如最大循環代數,若滿足設定的規則,就輸出最后篩選的種群當作最后進行計算的 Pareto 最優解; 否則返回選擇、交叉、變異繼續進行種群更新直到滿足終止條件。
結果分析
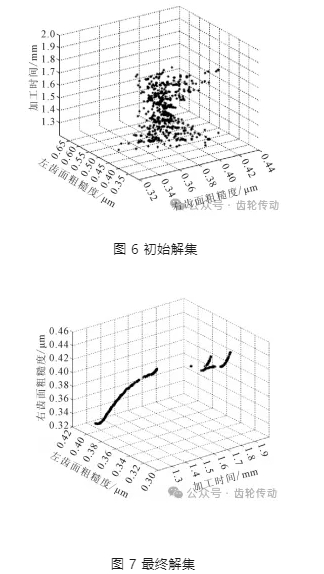
在 MATLAB 軟件里面進行算法運算,在種群為 500,運行次數為 2 000 的條件下得到初始解集如圖 6 所示,最終解集如圖 7 所示。從圖 6 可知,在給定的自變量取值空間內,值域分布較為分散,表明 500 個初始解對應的取值空間分散分布。圖 7 為算法運行的最終結果,可以看出值域分布比較集中,表明在多個目標之間相互制約的情況之下得到了一系列的解。
Pareto 最優解集只是為決策者提供了多種決策方案,為了使求解結果能更好地應用于實際,需要在眾多的非支配解集中選擇一個較優解作為最終解,即選取一個妥協解。妥協解取 Pareto 最優解中與理想解的相對距離最小解,稱為妥協系數,相應的函數表達式為:
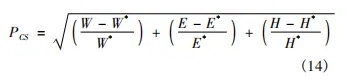
式中: PCS為妥協系數; (W,E,H) 為 Pareto 解的任意解; (W* ,E* ,H* ) 為理想解,其中 W* ,E* ,H* 分別表示以加工時間、左齒面粗糙度、右齒面硬度為單目標的最優解。
根據式(14) 計算妥協系數,取妥協系數最小對應的解為最優解。對于本次實驗結果,PCS最小值為 0.229 8,對應的 3 個函數值為 ( 1.290,0.385,0.359) 。優化前的參數與優化結果如表 9 所示。

從表9可知,優化后的加工參數得到的加工時間為 1.29 min,相比于實際加工時間減少了 30.19% 。左右齒面的粗糙度分別為左齒面從 0.400 μm下降到 0.385 μm; 右齒面從 0.380 μm 下降到 0.359 μm,都得到了一定程度的改善。
四、結論
針對齒輪的磨削加工過程對齒面粗糙度的影響問題,以蝸桿砂輪磨齒加工為例進行了實驗研究,分析了磨削加工參數與齒面粗糙度的關系,并建立了加工時間和粗糙度綜合優化目標模型,采用多目標非支配遺傳算法 NSGA - II 對蝸桿砂輪磨齒加工參數進行優化。通過研究得到如下結論:
(1) 在蝸桿砂輪磨齒加工過程中,砂輪線速度、砂輪軸向進給速度以及單側磨削深度 3 個加工參數對齒面粗糙度的影響呈現一種多元交互影響關系,并且加工參數對齒輪左右齒面的粗糙度的影響關系不同。
(2) 在砂輪磨齒加工過程中,砂輪軸向進給速度對左右齒面的粗糙度的影響在試驗范圍之內隨著進給速度的增加影響不大。軸向進給速度直接影響著加工效率,因此在一定范圍內可以考慮盡可能將其值設定大一些。
(3) 采用 NSGA - II 優化算法可以在獲得眾多的非支配解中獲得一個相對較優的解,推薦優化參數組能降低左右齒面的粗糙度,同時能提高 30.19% 的生產效率。
參考文獻略.
