齒輪傳動作為一種嚙合性能良好的傳動機構,在礦山機械領域應用廣泛。但礦用機械設備齒輪齒面的復雜接觸關系會造成輪齒的點蝕、膠合甚至折斷,導致齒輪失效和報廢,其都與齒輪接觸應力和彎曲應力的變化過程有關。而傳統的齒面接觸應力計算利用球接觸或圓柱體接觸理論,輪齒彎曲強度的計算是運用平板接觸理論或 30° 切線法,都只是靜態下的強度校核,不能夠完全反應嚙合齒輪動態狀況下的應力變化過程。有限元方法可以在動態因素的情況下對齒輪的嚙合全過程進行模擬,還可以迅速獲得齒輪接觸應力和齒根彎曲應力的變化過程,提高齒輪接觸應力和齒根彎曲應力的計算精度與效率。
本文采用 Creo2.0 軟件建立了某礦用直齒齒輪的三維參數化模型,并利用 ABAQUS 軟件中子模型技術對齒輪嚙合處的接觸應力和齒根處的彎曲應力進行詳細分析,為實現齒輪參數化、系列化設計提供一種新方法。
一、齒輪參數化設計
Creo2.0 是一種應用于 CAD/CAE/CAM 的軟件。基于 Creo 的齒輪參數化設計是采用幾何建模、數學方程及關系控制來實現的。
(1)漸開線直齒圓柱齒輪是一種應用比較廣泛的齒輪,其建模過程中主要考慮的因素有模數 m、齒數 z、壓力角 α、齒寬 b、齒頂高系數 ha* 、頂隙系數 c* 、變位系數 x。
(2)通過已知參數可確定其他幾何參數。設 d 為分度圓直徑,da 為齒頂圓直徑,db 為基圓直徑,df 為齒根圓直徑,ha 為齒頂高,hf 為齒根高。各參數關系式

(3)通過幾何參數建立模型的特征參數,從而形成完整的齒輪幾何模型。設 θ 為漸開線展開角,t 為 0~1 的一個變量,r 為基圓半徑,x、y、z 分別為 X、Y、 Z 軸的值。笛卡爾坐標系中漸開線方程為

在 Creo 中輸入參數可以生成大、小齒輪,并對大、小齒輪采用銷釘約束方式裝配,保存為.stp 格式,導入 ABAQUS 中。
二、齒輪嚙合有限元分析
(1)材料參數
選用材料均為 40Cr 的大、小嚙合齒輪為研究對象,設置彈性模量 206 GPa、泊松比 0.3、密度 7.9× 10-9 t/mm3 。
(2)齒輪參數及工況設置
大、小齒輪的基本參數:

相嚙合的齒輪工況為:小齒輪為主動輪,大齒輪為從動輪;輸入功率為 27.7 kW,主動輪轉速 311 r/min,從動齒輪所受扭矩 820 N·m,工作壽命 1 000 h,傳動比 3.2;齒輪結合采用“面—面”接觸,小齒輪為主面,大齒輪為從面;對大、小齒輪參考點約束 5 個方向的自由度(U1=U2=U3=UR1=UR2=0),小齒輪參考點 施加旋轉速度 VR3=32.55 rad/s,大齒輪參考點施加沿 Z 軸的扭矩 820 N·m,并分別對大、小齒輪參考點與大、小齒輪內圈進行耦合。
(3)有限元模型
利用顯式非線性動力有限元分析軟件 ABAQUS/ Explicit 進行三維動力接觸有限元分析。為了準確獲得齒輪接觸應力,輪齒模型部分需要較細的有限元網格,而且考慮到加速度和轉動慣量的影響,在仿真過程中需要運用全齒模型,但會造成整個齒輪的單元數過多,計算時間過長。為了保證精度且節約計算成本,本文采用子模型技術,即截取 5 齒模型來計算接觸應力和彎曲應力的變化,對子模型采用 6 面體單元(C3D8R)進行網格細化。
三、仿真計算結果分析
(1)接觸應力計算結果分析
①齒輪在嚙合過程進行三維顯示非線性動力有限元分析,接觸應力分布變化過程如圖 1 所示。
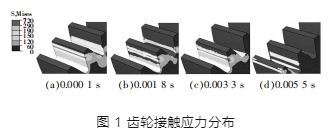
由圖 1 可知,當齒輪進入嚙合狀態時,輪齒在單齒嚙合和雙齒嚙合之變換。在雙齒嚙合狀態傳動時,齒輪之間的接觸應力值較小;當單齒嚙合狀態傳動時,齒輪之間的接觸應力值較大。在雙齒嚙合狀態下傳動時,由于 2 個齒牙之間載荷分布是變化的,中間的齒隨著傳動方向逐漸成為承載齒輪,其接觸應力隨之升高,當后 1 對輪齒進入嚙合后,接觸應力隨之降低。
②齒輪嚙合中的 1 對輪齒嚙合過程進行三維顯式非線性動力有限元分析,接觸應力變化曲線變化曲線如圖 2 所示。
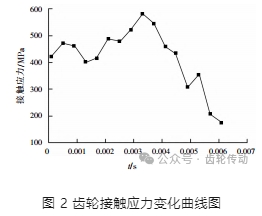
由圖 2 可知,在單、雙齒輪交替嚙合處,單齒接觸應力相對于雙齒嚙合應力變化較大;在雙齒嚙合區,輪齒的最大接觸應力相對比較平穩,該現象說明雙齒嚙合區的嚙合沖擊力相對較小。
③1 對齒輪在嚙合狀態下進行三維顯示非線性動力有限元分析,嚙合面的接觸應力最大值如圖 3 所示。
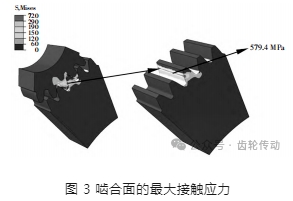
由圖 3 可知,該嚙合齒輪的最大接觸應力出現在節圓附近單齒嚙合區,最大接觸應力 579.4 MPa。
(2)齒根彎曲應力計算結果分析
①齒輪嚙合中的 1 對輪齒嚙合過程進行三維顯式非線性動力有限元分析,得到齒根彎曲應力分布變化過程如圖 4 所示,彎曲應力變化曲線如圖 5 所示。

由圖 4 和圖 5 可知,隨著嚙合點從齒頂向齒根移動,輪齒的齒根彎曲應力逐漸升高,在輪齒上界點附近,齒根彎曲應力達到最大,然后逐漸下降,并隨著 1 對齒輪和 2 對齒輪的嚙合狀態周期性變化而產生波動。在輪齒離開嚙合時,齒根彎曲應力迅速降低。
②1 對齒輪在嚙合狀態下進行三維顯示非線性動力有限元分析,得到齒輪齒根彎曲應力最大值的嚙合位置,如圖 6 所示。

由圖 6 可知,齒輪齒根最大彎曲應力出現在大齒輪上界點附近,最大彎曲應力 242.1 MPa。
四、接觸應力和彎曲應力理論計算
(1)齒輪接觸應力計算
接觸應力計算公式以兩曲面赫茲接觸應力公式為基礎。載荷系數

有限元計算出齒輪最大接觸應力 579.4 MPa,理論計算結果為 647.51 MPa,說明了有限元模型計算的正確性,赫茲理論計算偏向于保守。
(2)齒輪彎曲應力計算
齒輪的彎曲應力與齒輪齒根過渡圓弧處及齒輪危險截面抗斷裂的能力有關。標準的彎曲應力計算基于平板理論,即按全部載荷作用于 1 對齒嚙合區齒頂時,直齒輪齒根最大彎曲應力

有限元計算齒輪齒根最大彎曲應力為 242.1 MPa,由平板理論計算結果為 227.67 MPa,說明了有限元模型計算的正確性。
五、結語
(1)在齒輪嚙合過程中,最大接觸應力出現在單齒嚙合區節圓附近,最大彎曲應力出現在嚙合區上界點,最大接觸應力和最大彎曲應力與理論計算結果相近;
(2)齒輪單齒嚙合和雙齒嚙合過程中輪齒的接觸應力值是起伏變化的,單齒嚙合較雙齒嚙合接觸應力有所增加;
(3)在單、雙齒交替嚙合處,單齒接觸應力較雙齒嚙合應力變化較大,當齒輪進入到雙齒嚙合區域時,其最大接觸應力運行較為平穩,嚙合沖擊不大。
參考文獻略.
