為了解決傳統齒輪承載接觸分析力學解析方法難以考慮齒廓修形的問題，以齒廓修形漸開線直齒輪為研究對象，基于時變嚙合剛度，提出了一種齒輪承載情況下齒間載荷分配系數與齒面接觸應力解析算法。通過對比齒輪承載接觸時接觸點在嚙合線方向的變形量與修形量，提出修形齒輪單雙齒嚙合狀態判定方法，并計算不同狀態下的嚙合剛度; 推導修形齒輪的嚙合力、剛度與變形的力學關系，建立各嚙合齒對的齒間載荷分配系數計算模型，應用赫茲接觸理論求解齒面接觸應力; 分別在不同修形高度、修形曲線與配對齒數情況下，計算分析多種齒廓修形算例的齒間載荷分配系數與齒面接觸應力。結果表明，解析算法求解的齒間載荷分布系數、齒面接觸應力及相應單雙齒嚙合區間與有限元結果相一致，相對誤差較小，證明了該算法有較高的精度與穩定性，為齒廓修形齒輪承載接觸分析提供一種高效便捷的新方法。

　　輪齒承載能力是評價齒輪傳動品質的一項重要標準，齒間載荷分配系數和面接觸應力的模型精度是齒輪承載接觸力學計算結果精確性的前提與關鍵。齒輪修形可以有效改善齒輪動載荷變化梯度，減少沖擊、振動與噪音，對提高齒輪傳動品質有十分重要的作用。然而，已有的齒輪承載接觸分析力學解析模型大都只能考慮鼓形的齒向修形，較難計入齒廓修形的影響。

　　對于齒輪承載過程中產生的齒面接觸應力，學者常采用有限元法和解析法。其中，有限元法建模精度高，且計算結果精確，因而得到較為廣泛的應用。朱才朝利用基于勢能法的三段函數式齒間載荷分配系數模型分析齒輪的彈流潤滑特性; AZNAR 等采用 MPC 算法與局部網格細化法優化齒輪的承載接觸有限元模型，提高了計算精度與效率; MAPER 等建立了包含齒廓修形的漸開線直齒圓柱齒輪承載接觸有限元模型; 唐進元等利用有限元分析了正交面齒輪的重合度、載荷分布、接觸應力等承載接觸性能參數; 白恩軍等建立了斜齒圓柱齒輪承載接觸有限元模型。然而，有限元算法計算精度依賴于模型的網格質量和局部網格細化程度，存在計算效率低、收斂難的問題。

　　相較于有限元法，基于赫茲彈性接觸理論的力學解析算法，計算快捷高效受到了越來越多的關注與研究。王會良等基于齒輪 TCA 法和齒面柔度系數，分析齒輪承載接觸特性，建立了齒輪 LTCA 理論; 曹雪梅等提出一種簡化輪齒接觸分析中非線性方程數量的分解算法，提高了計算效率; 王羽達等基于輪齒 TCA 模型和赫茲接觸理論，計算了漸開線齒輪的動態接觸應力。

　　綜上所述，傳統齒間載荷分配系數解析建模未考慮齒廓修形及其引起的單雙齒接觸區域變化，無法準確計算承載嚙合齒對的齒間載荷分配系數與齒面接觸應力，同時，LTCA 方法大都僅在 TCA 分析階段考慮齒廓修形，而在齒面柔度系數或承載接觸分析時采用有限元方法。為此，本文以齒廓修形的漸開線直齒輪為研究對象，提出修形齒輪單雙齒嚙合狀態的 s 判定方法與相應的嚙合剛度計算方法，建立更為精確的修形齒輪齒間載荷分配系數與齒面接觸應力解析算法，對不同修形高度、修形曲線與配對齒數條件下的齒輪算例進行承載接觸分析，并與同參數下的有限元結果進行對比，驗證解析算法的精度與穩定性。

　　一、齒廓修形的漸開線直齒輪模型

　　為建立齒廓修形漸開線直齒輪的齒廓曲線方程，需確定齒廓最大修形量 Δ_maxi、修形高度 h、修形曲線，根據文獻最大修形量 Δ_maxi為:

　　式中: Δ_maxi、c_i 分別為最大修形量與修形修正量(i 為 1、2，用以區分參與嚙合的主/從動輪) ，相應的主/從動輪修形修正量 c₁、c₂ 分別取 9 與 4 ，F_t 為接觸點的圓周力，B 為齒輪寬度。

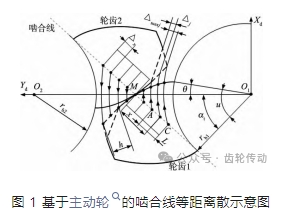
　　建立坐標系 X_dOY_d，如圖 1 所示，以 Δ_x 作為增量等距離散嚙合線，并在圓周方向上計算出輪齒 1 上的齒廓對應點，若該點位于修形齒廓區域內，嚙合線離散點的齒廓對應點處的修形量 Δ_j 為:

　　式中: 修形曲線變化系數 k 由選取的修形曲線確定，Linear、Yoshio、Walker 與拋物線修形曲線變化系數 k 分別為 1.0、1.2、1.5 與 2.0，x 為嚙合點 M 在嚙合線方向上距離單雙齒變化點 A 的距離，L 為輪齒 2 的修形區域在高度方向上對應至嚙合線 A 點至 C 點的線段長度( 長修形) ，C 點為輪齒 1 的嚙合起始點; 另外，根據文獻，正弦修形曲線的嚙合點修形量為:

　　確定齒廓對應點處的修形量 Δ_j 后，根據漸開線齒廓曲線展成原理，可建立修形齒廓曲線參數方程為:

　　式中: u 為嚙合線離散點對應漸開線齒廓處的參角，u = θ + α_t，θ 為嚙合點處展角，α_t 為壓力角。

　　二、修形齒輪單雙齒嚙合狀態判定與嚙合剛度

　　標準漸開線齒輪副在承載嚙合傳動過程中齒輪嚙合剛度主要包括 3 部分: 輪齒剛度(彎曲剛度 k_b、剪切剛度 k_s 與徑向壓縮剛度 k_a ) 、齒輪接觸剛度 k_c 與齒輪基體剛度 k_f。單齒嚙合剛度 K_i 為上述各剛度的串聯形式，雙齒嚙合剛度 K_all為兩對輪齒嚙合剛度的并聯形式。

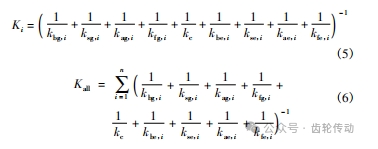
　　式中: i 為 1、2，用于區分參與嚙合的不同齒對，下標 g、e 分別表示主動輪與從動輪。

　　當采用齒廓修形時，原單齒嚙合區間的齒輪嚙合剛度根據式(5) 進行計算，原雙齒嚙合區間由于修形齒廓參與嚙合，嚙合狀態會發生變化，需要重新判定嚙合狀態: 根據齒對嚙合力與嚙合剛度計算接觸點處沿嚙合線方向的變形量，然后與接觸點處修形量進行對比，基于二者的大小關系判定修形齒輪副的單雙齒嚙合狀態，并計算單雙齒的嚙合區間與嚙合剛度，其中，修形齒輪嚙合剛度定義為 K_TPM。

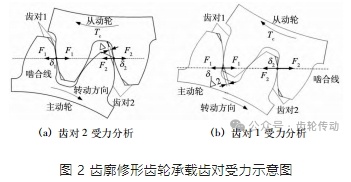
　　如圖 2a 所示，當主動輪順時針轉動時，齒對 1 首先進入嚙合承擔載荷，由于齒對 2 主動輪處存在修形齒廓，當齒對 1 沿嚙合線方向的變形量 δ₁ 大于齒對 2 處主動輪的齒廓修形量 Δ₁ 時，齒對 2 將進入嚙合并參與傳動，此時兩對輪齒共同承擔負載扭矩 T_c，并在嚙合線方向上的兩處作用點產生嚙合力 F₁、F₂，根據力矩平衡和廣義胡克定律可得:

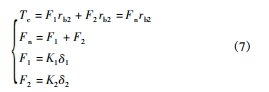
　　式中: K₁、K₂ 與 δ₁、δ₂ 分別為齒對 1、齒對 2 的單齒嚙合剛度與接觸點沿嚙合線方向的變形量，r_b2為從動輪的基圓半徑。

　　與此同時，齒對 1 沿嚙合線方向的變形量 δ₁ 即為整體嚙合變形量 δ_all，則 δ_all = δ₁ > δ₂，相應的修形齒輪嚙合剛度 K_TPM為:

　　式中: F_n 為齒輪副法向力，根據式(7) 將式(8) 推導為:

　　同時，齒對 2 在嚙合點處嚙合變形量 δ₂ 與修形量 Δ_j 之和等于齒對 1 處嚙合變形量為 δ₁。

　　將式(10) 帶入式(9) ，可得到:

　　將式(8) 轉化為關于變形量 δ₁ 的表達式，并代入式(11) ，可推導得出圖 2a 所示齒對承載接觸狀態下的修形齒輪嚙合剛度 K_TPM，即式(12) 中條件為 δ_all = δ₁ > _δ2 的表達式; 同樣地，如圖 2b 所示的齒對承載接觸狀態，此時齒對 2 沿嚙合線方向的變形量 δ₂ 即為整體嚙合變形量 δ_all，即 δ_all = δ₂ > δ₁，同理可推導出相應的修形齒輪嚙合剛度 K_TPM，即式(12) 中條件為 δ_all = δ₂ > δ₁ 的表達式。因此，圖 2 所示齒對承載接觸狀態下的修形齒輪嚙合剛度 K_TPM可寫為:

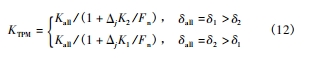
　　式(12) 即為齒廓修形漸開線直齒輪的嚙合剛度分析方法，下文將建立單雙齒嚙合狀態的判定模型，確定實際雙齒嚙合區間，然后依據式(12) 計算雙齒區間內的齒輪嚙合剛度。

　　如圖 3 所示，基于主動輪齒廓，對齒輪副嚙合區間進行劃分，分析齒對 1、2 的接觸嚙合狀態及相應的嚙合剛度，點 a₁ 為嚙入點，點 a₃、a₄ 為單雙齒嚙合變化點，點 a₂、a₅ 為原雙齒接觸區域平分點，點 a₁ ～ 點 a₅ 將接觸區域劃分為 A₁、A₂、A₃、A₄、A₅。

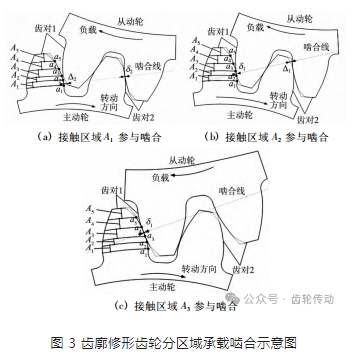
　　如圖 3a 所示，當齒對 1 以 a₁ 點即將進入接觸區域 A₁ 參與嚙合時，齒對 1 中從動輪待接觸區域存在修形齒廓，若齒對 2 沿嚙合線方向的變形量 δ₂ 大于齒對 1 中從動輪修形量 Δ₂，則齒對 1 接觸參與嚙合，即為雙齒嚙合狀態，此時的修形齒輪嚙合剛度 K_TPM可依據式 (12) 計算; 若齒對 2 沿嚙合線方向的變形量 δ₂ 小于齒對 1 中主動輪修形量 Δ₂，則齒對 1 不參與嚙合，此時為單齒嚙合狀態(齒對 2 單獨承載) ，齒對 2 的嚙合剛度 K₂ 依據式(5) 進行計算。

　　如圖 3b 所示，當齒對 1 以 a₂ 點即將進入接觸區域 A₂ 參與嚙合時，齒對 2 中主動輪待接觸區域存在修形齒廓，若齒對 1 沿嚙合線方向的變形量 δ₁ 大于齒對 2 中主動輪修形量 Δ₁，則齒對 2 接觸參與嚙合，即為雙齒嚙合狀態，此時的修形齒輪嚙合剛度 K_TPM可依據式 (17) 計算; 若齒對 1 沿嚙合線方向的變形量 δ1 小于齒對 2 中主動輪修形量 Δ1，則齒對 2 不參與嚙合，此時為單齒嚙合狀態(齒對 1 單獨承載) ，齒對 1 的嚙合剛度 K1 依據式(5) 進行計算。

　　如圖 3c 所示，當齒對 1 以 a₃ 點即將進入接觸區域 A₃ 參與嚙合時，此時接觸區域 A₃ 為單齒嚙合狀態，齒對 1 的嚙合剛度依據式(5) 進行計算。

　　綜合圖 3 所述，即可得到齒廓修形齒輪在各嚙合位置的單雙齒嚙合狀態判定與相應嚙合剛度計算方法。

　　三、齒廓修形漸開線直齒輪承載接觸分析

　　齒間載荷分配系數

　　未修形齒輪的齒間載荷分配系數：根據式(6) 確定的雙齒嚙合剛度 K_all與齒輪整體變形量 δ_all，法向力 F_n 可表示為:

　　根據式(7) 中確定的載荷、剛度以及變形關系，帶入式(13) 等式左側，可推導出:

　　由于嚙合齒對在嚙合線方向上變形量 δ₁、δ₂ 中的較大值與雙齒嚙合整體變形量 δ_all相等，此時無論δ_all = δ₁≥δ₂ 或 δ_all = δ₂≥δ₁，根據式(14) 皆可推導出各嚙合齒對在嚙合線方向上的變形量 δ₁、δ₂ 與雙齒整體嚙合變形量 δ_all相等，即:

　　進一步可根據式(7) 中嚙合力、剛度與變形的數學關系推導出:

　　式中: F_i 為接觸齒對的嚙合力( i 為 1、2) 。

　　對式(16) 進行比例互換，可得到未修形下的齒輪齒間載荷分配系數 S 為:

　　齒廓修形齒輪的齒間載荷分配系數：當齒廓修形后，原雙齒嚙合區域的嚙合狀態發生變化，根據標準漸開線齒輪時變嚙合剛度式(5) 與齒廓修形齒輪嚙合剛度式(12) ，重新確定齒輪的單雙齒嚙合狀態與相應嚙合剛度，繼而根據式(17) 計算修形齒輪不同齒廓區域參與嚙合的齒間載荷分配系數 SLDF。根據圖 3，以齒對 1 為例，分析齒對 1 承載嚙合下的齒間載荷分配情況，具體為:

　　式中: K_u 為齒對 1 的嚙合剛度，當齒對 1 處于單齒嚙合狀態時，其嚙合剛度依據式(5) 計算，即 K_u = K₁ ; 當齒對 1、2 同時參與嚙合時，此時計算 K_u 需考慮齒對 2 嚙合剛度 K₂ 的疊加影響，即:

　　當齒對 1 在齒廓區域 A₁ 處嚙合時，由于齒對 2 接觸變形量 δ₂ 的影響，齒對 1 存在非接觸與接觸兩種狀態，若 δ₂ > Δ₂，則齒對 1 接觸，此時為雙齒嚙合狀態，將式(18) 代入式(19) 可得到齒對 1 的齒間載荷分配系數 S_LDF。

　　若 δ₂ < Δ₂，則齒對 1 為非接觸狀態，此時齒對 1 不分擔載荷，則齒間載荷分配系數為 0，即:

　　當齒對 1 在齒廓區域 A₂ 處嚙合時，由于齒對 1 接觸變形量 δ₁ 的影響，齒對 2 存在非接觸與接觸兩種嚙合狀態，若 δ₁ > Δ₁，則齒對 1 接觸，此時為雙齒嚙合狀態，齒對 1 的嚙合齒廓為非修形區域，其齒間載荷分配系數根據式(22) 進行計算。

　　若 δ₁ < Δ₁，則齒對 2 為非接觸，此時齒對 1 承擔全部載荷，齒間載荷分配系數為 1，即:

　　當齒對 1 在齒廓 A₃ 處嚙合時，此時為單齒嚙合區域，齒間載荷分配系數為 1，即:

　　當齒廓進入 A₄、A₅ 段參與嚙合時，齒對 1 皆為非修形齒廓參與嚙合，此時僅考慮齒對 1 的嚙合剛度，即 K_u = K₁，相應的齒間載荷分配系數為:

　　綜上所述，在一個嚙合周期內，根據齒對 1 在齒廓區域 A₁、A₂、A₃、A₄、A₅ 是否接觸參與嚙合及其嚙合狀態判定，計算參與嚙合齒對的嚙合剛度，根據式(18) ～ 式(25) ，可得到修形漸開線直齒輪齒間載荷分配系數 S_LDF計算模型。

　　齒面接觸應力

　　根據上述建立的修形齒輪齒間載荷分配系數模型，可計算嚙合力 F_i，繼而根據赫茲接觸理論計算齒面接觸應力。

　　首先，需確定不同齒廓赫茲接觸類型下接觸點處的綜合曲率半徑 R_e，針對未修形的齒廓區域，根據歐拉薩瓦利公式，通過計算沿嚙合線方向上基圓至嚙合點的距離求得其曲率半徑 ρ₁、ρ₂，對于齒廓修形區域，以主動輪為例，根據微分幾何與修形齒廓方程式 (4) ，可推導出修形齒廓曲率 C_TPM與曲率半徑 ρ_TPM。

　　針對齒廓修形齒輪承載嚙合時存在的不同赫茲接觸類型，可推導出相應的綜合曲率半徑 R_e。

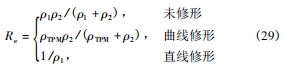
　　通過式(26) 確定的齒間載荷分配系數 S_LDF，可計算出參與嚙合齒對的接觸力 F_i，根據式(29) 所得綜合曲率半徑 R_e，基于赫茲彈性接觸理論，可推導出修形齒輪承載接觸時的齒面接觸應力 σ_H 與接觸半寬 b。

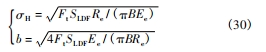
　　式中: E_e 為綜合彈性模量，具體表達式為:

　　式中: E₁、E₂ 與 ν₁、ν₂ 分別為主、從動輪的彈性模量與泊松比。

　　如圖 4 所示為該解析算法的流程圖。

　　四、計算結果分析與討論

　　基于上述建立的算法，求解不同修形高度、修形曲線與配對齒數 3 種條件下不同算例的齒間載荷分配系數與齒面接觸應力，并與同參數下的有限元計算結果進行對比評價，驗證本文解析算法計算結果的準確性和穩定性。基于表 1 中拋物線修形齒輪的主要幾何參數，每種條件下選取 5 個算例求解以上不同齒廓修形齒輪算例的齒間載荷分配系數(圖 5 ～ 圖 7) 和齒面接觸應力(圖 12 ～ 圖 14) 。使用有限元法對比評價解析 算法結果的準確性和穩定性，以驗證算法的正確性。

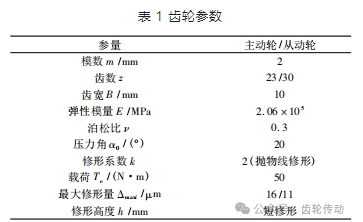
　　分析如圖 5 ～ 圖 7 所示的齒間載荷分配系數結果可知:

　　(1) 本文解析算法與有限元兩種計算方法的齒間載荷分配系數具有相同變化趨勢: 由最小值逐漸增大至最大值 1，此過程為雙齒嚙合區間; 隨后進入單齒嚙合區間，即 S_LDF = 1 的水平線; 再進入雙齒嚙合區，下降至最小值。同時嚙合線各點所對應的誤差數值較小。

　　(2) 根據圖 5 ～ 圖 7 數據結果，可得到不同齒廓修形算例在一個嚙合區間內的齒間載荷分配系數誤差均值，如圖 8 所示，每種條件下 5 個算例誤差均值變化范圍分別為 7.5% ～ 9.2%、7.5% ～ 8.0%、5.6% ～ 7.8%， 表明誤差均值較小且不同算例的誤差均值相近。算例結果分析表明，對于不同算例情況下的齒輪副，本文解析算法的齒間載荷分配系數計算精度較高，且算法具有較好的誤差穩定性。

　　(3) 根據圖 5 ～ 圖 7 數據結果，分析齒廓修形后每個算例的單齒嚙合區位置誤差，以此可進一步評價解析算法的計算精度。其中，齒廓修形后的單齒嚙合區起始點位置誤差、結束點位置誤差與嚙合區間位置誤差分別如圖 9 ～ 圖 11 所示。不同修形高度、修形曲線 與配對齒數算例的單齒嚙合區起始誤差變化范圍分別為 5.8% ～12.4%、5.1% ～14.2%、5.8% ～10.1%，單齒嚙合區結束點位置誤差變化范圍分別 9.2% ～ 13.1%、 6.1% ～13.3%、9.7% ～ 12.6%，單齒嚙合區間位置誤差變化范圍分別為 3.2% ～12.5%、3.2% ～ 13.0%、2.2% ～ 8.8% ，表明解析算法所得出的單雙齒變換點及其區間大小與有限元結果之間誤差較小，可較為準確地計算出單雙齒嚙合變換點以及嚙合區間位置。因此，本文解析算法中依據修形量與變形建立的單雙齒嚙合區間判定方法具有較高的計算精度，可較為準確的計算單雙齒變換點以及嚙合區間位置。

　　(4) 另外，由于配對齒數的變化，齒輪副有效嚙合區間也會隨之變化，分析圖 7 中得到的橫坐標實際嚙合線長度可得到齒廓修形齒輪的有效嚙合區間，相對于有限元結果，5 個配對齒數算例的有效嚙合區間誤差分別為 1.3% 、1.0% 、3.0% 、3.1% 、1.1% ，相對誤差較小，表明本文解析算法對不同配對齒數的齒輪副嚙合區間計算結果的準確度較高。

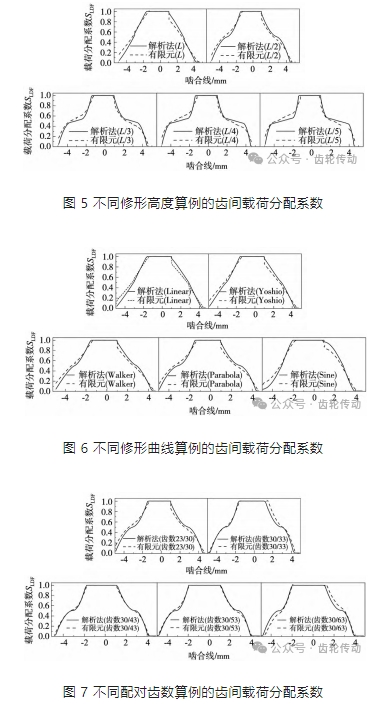
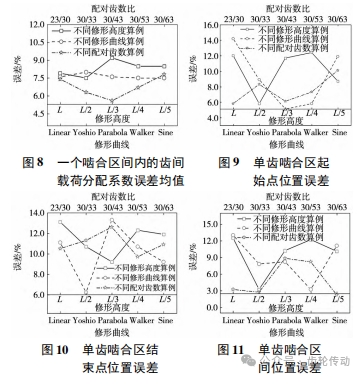
　　分析如圖 12 ～ 圖 14 所示的 4 種條件下不同齒廓修形算例在一個嚙合區間內的齒面接觸應力結果可知:

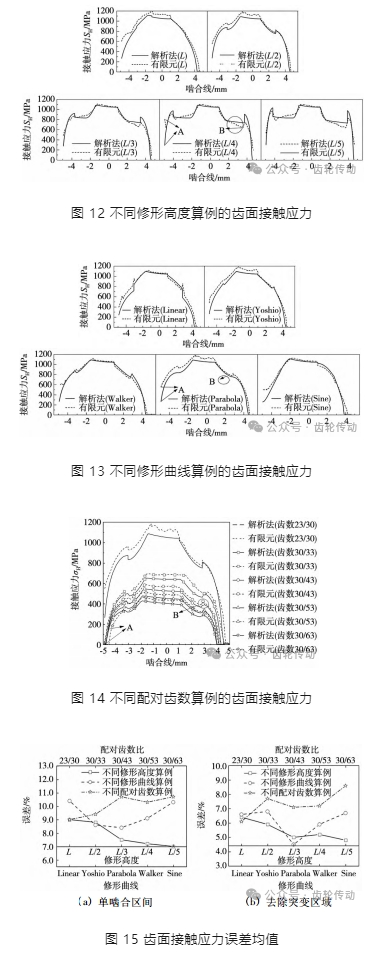
　　(1) 解析算法的齒面接觸應力結果與有限元結果在變化趨勢具有較好的一致性; 根據圖 12 ～ 圖 14 的齒面接觸應力結果，可得到 3 種條件下齒廓修形算例在一個嚙合區間內的齒面接觸應力誤差均值( 圖 15a) 變化范圍分別為7.0% ～ 9.0%、8.4% ～ 10.4%、9.0% ～ 10.7%，誤差均值較小，同時不同算例間誤差均值相近，表明解析算法具有較高的齒面接觸應力計算精度與誤差穩定性。

　　(2) 與此同時，在修形齒輪剛開始進入嚙合、即將退出嚙合以及修形曲線與漸開線過渡區域，有限元結果產生了局部應力突變，以圖 12 ～ 圖 14 中的 A、B 區域為例，主要由以下兩個原因導致: ①剛開始嚙入與即將退出嚙合時，接觸齒對嚙合力較小，需要極小網格尺寸( 低于微米 1 ～2 個量級) 才能有效捕捉到該處的接觸應力信息，建模困難，且嚙入時齒頂部位存在幾何尖點; ②修形齒廓過渡區域對幾何曲率產生一定程度的嚙合畸變。因此，當求解步長位于上述位置附近時會直接影響有限元計算結果，導致有限元局部應力突變、計算誤差較大，這是不可避免的。除去由有限元結果突變區域所帶來的計算誤差后，解析算法的齒面接觸應力在一個嚙合區間內的誤差均值(圖 15b) 變化范圍分別為 4.8% ～ 6.4% 、4.5% ～ 6.8% 、6.1% ～ 8.6% ，再次表明解析算法具有較高的齒面接觸應力計算精度與誤差穩定性。

　　五、結論

　　(1) 本文針對齒廓修形的漸開線直齒輪，通過對比承載齒輪接觸點沿嚙合線方向的變形量與修形量，得到了修形齒輪單雙齒嚙合狀態的判定方法與相應嚙合剛度的計算方法，通過推導修形齒輪嚙合力、剛度與變形的力學關系，建立了修形齒輪各嚙合齒對精確的 齒間載荷分配系數計算模型。

　　(2) 基于齒間載荷分配系數計算了嚙合齒對實際承擔載荷，應用歐拉薩瓦利公式和赫茲接觸理論，建立了齒廓修形齒輪嚙合過程中的齒面接觸應力模型。

　　(3) 不同修形高度、修形曲線與配對齒數條件下多種齒廓修形齒輪的算例結果表明: 本文所提出解析算法的齒間載荷分配系數、齒面接觸應力與相應單雙齒嚙合區間結果與有限元方法結果變化規律相一致，相對誤差較小，具有較高的計算精度與穩定性，為齒廓修形漸開線直齒輪的承載接觸分析提供了一種高效便捷的新方法。

　　參考文獻略.