螺旋傘齒輪以高傳動比、低噪聲及大傳遞轉矩等優點廣泛用于重型車輛的傳動系統中。“銑齒—熱處理—磨齒”是目前齒輪加工中普遍采用的生產流程。磨削作為齒輪生產制造環節中的最后一步,磨削表面完整性對齒輪的使用壽命具有極大的影響。磨削表面形貌是表面完整性的重要指標之一,對齒輪的耐磨性、抗疲勞強度及接觸應力等起著關鍵作用。
通過研究砂輪磨粒和工件表面幾何上的相互作用,建立磨削表面三維形貌仿真模型,可以預測和分析不同磨削工藝參數下加工工件表面形貌特征。許多研究學者對其開展深入的研究工作,并取得一些顯著性成果。MALKIN詳細闡述磨削過程中砂輪磨粒的運動軌跡,磨粒和被加工工件的相互作用以及切屑的生成機制,給出磨削參數對切削厚度的影響規律。CHEN 等研究磨削表面形貌的生成方法,并對磨削過程中的磨削力進行仿真分析,并通過試驗驗證所提理論模型的正確性。BUTLER 等采用三維測量技術對砂輪形貌進行測試,研究磨損砂輪和未磨損砂輪表面形貌的特點,以及不同砂輪磨削加工工件和砂輪形貌的關系。ZHOU 等根據實際砂輪表面磨粒形狀、大小和分布密度不同的情況,指出砂輪表面磨粒高度呈隨機的高斯分布狀態。NGUYEN 等給出砂輪表面每個磨粒的切削軌跡,并將其映射到工件表面坐標系,取工件表面上每一點上所有磨粒軌跡的最小值,即得磨削加工后的工件表面的三維形貌。陳東祥等基于 JOHNSON 變換和線性濾波技術,生成不同統計學特征的砂輪形貌。根據磨削運動學,提出超精密磨削加工工件表面的仿真模型。鞏亞東等為考慮砂輪與工件軸線之間夾角 α 對工件表面粗糙度的影響,基于砂輪表面磨粒的分布狀態和磨粒運動學特征,給出點磨削工件表面三維形貌的生成模型。呂長飛等采用 JOHNSON 變換和 GABOR 小波變換在隨機域內對磨削砂輪形貌進行仿真,并給出外圓磨削仿真模型,實現對加工工件形貌的仿真和粗糙度預測。
綜上所述,雖然許多學者開展磨削加工工件表面形貌的仿真研究,但是較多以平面磨削、外圓磨削、點磨削等定曲率軌跡磨削為主。而螺旋傘齒輪磨削時,工件基于所設定的空間軌跡進行運動,其運動軌跡的曲率發生顯著變化,從而影響砂輪磨粒在工件表面的切削干涉軌跡。因此,為了對螺旋傘齒輪磨削表面形貌進行預測,首先分析螺旋傘齒輪磨削磨粒運動學,然后建立砂輪表面形貌特征模型,最后利用磨削試驗對所提出的模型進行驗證,并對比分析磨削參數對螺旋傘齒輪磨削表面形貌的影響規律。
一、螺旋傘齒輪磨削磨粒運動學分析
普通平面磨削磨粒運動軌跡
螺旋傘齒輪的磨削加工是一個非常復雜的材料去除過程,為了簡化分析的復雜性,進行如下假設:① 砂輪包絡面修整為理想形貌;② 不考慮砂輪振動對工件表面形貌生成的影響;③ 當砂輪進給時,與磨粒切削刃接觸的工件材料被完全去除;④ 不考慮測流和切屑瘤等現象。
在磨削過程中,由于磨粒沿砂輪徑向的高度分布不均,導致不同磨粒切削軌跡分布在不同直徑的同心圓上。單顆磨粒沿磨削路徑在齒輪表面留下高低不平的切削痕跡,若干個磨粒在齒輪表面的切削痕跡相互疊加,形成了齒面最終磨削表面形貌。研究每顆磨粒的切削模型,并通過推導與變換獲得其在齒面的運動軌跡。
在普通平面磨削過程中,單顆磨粒運動幾何模型如圖 1 所示,建立砂輪坐標系 o′x′y′z′和工件坐標系 oxyz。圖 1 中 oxyz 固定在工件的加工表面并與砂輪周邊最低處的磨粒位置重合。磨粒的運動軌跡 aob 由砂輪轉動和工件平動所合成。根據圖 1 中磨粒與工件之間的幾何位置關系,磨粒 G 的運動軌跡方程如式(1)所示
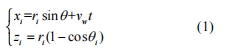
式中,xi、zi 為磨粒 G 的瞬時坐標,θ 為磨粒轉過相對角度,i 為工件沿 x 方向離散的點數,ri 為磨粒切削刃頂點至砂輪中心的距離,ns 為砂輪轉速,vw 為工件速度。磨削方式為逆磨,若磨削方式為順磨,則工作臺的進給速度方向取反。
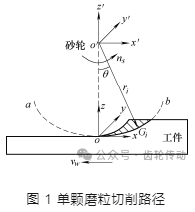
根據磨削過程運動學理論,可得磨粒 G 的運動軌跡為
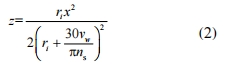
砂輪磨削工件時,磨粒依次進入磨削區切割工件表面,后進入磨削區的磨粒對先前磨粒切削后的表面進行再次切削,因此需要對相鄰磨粒的運動軌跡進行研究。相鄰磨粒的運動軌跡如圖 2 所示。假設磨粒 G1 的局部坐標系為 ox1y1z1坐標原點 o1與全局坐標系 oxyz 的原點重合,磨粒 G2 的局部坐標系為 o2x2y2z2。磨粒 G1 的運動軌跡為
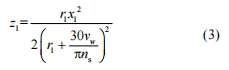
式中,r1 為磨粒 G1到砂輪中心的距離。
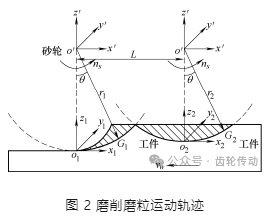
由于局部坐標系 o1x1y1z1 與全局坐標系 oxyz 重合,所以磨粒 G1 在全局坐標系 oxyz 中的軌跡方程為
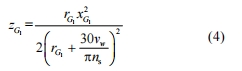
磨粒 G2 在局部坐標系 o2x2y2z2下的運動軌跡方程為
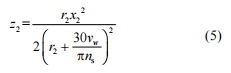
式中,r2 為磨粒 G2 到砂輪中心的距離。
砂輪中心移動距離 L 所需的時間與兩顆相鄰磨粒的工作時間間隔 Δt 相等,則
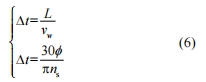
式中,φ 為相鄰磨粒的夾角。可得
磨粒 G2在全局坐標系 oxyz 下的運動軌跡方程為
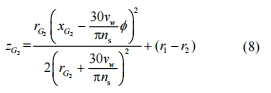
第 i 顆磨粒 Gi 在全局坐標系 oxyz 下的運動軌跡方程為
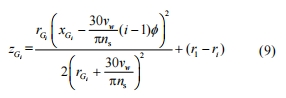
螺旋傘齒輪磨削磨粒運動軌跡
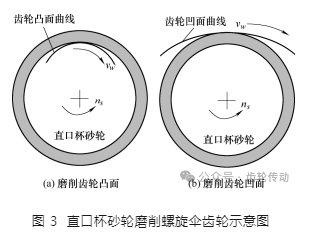
螺旋傘齒輪以“假想產型輪”原理進行加工,即通過假想產型輪與被切齒輪進行無隙的嚙合,代表產型輪的砂輪在被切齒輪工件上加工出所需齒形。直口杯砂輪的內外錐面的包絡面被修整為與螺旋傘齒輪凸面及凹面完全重合。磨削時,直口杯砂輪繞主軸以設定的磨削速度高速旋轉,同時螺旋傘齒輪工件以設定的展成速度按特定的軌跡相對直口杯砂輪運動,其凸面、凹面分別與砂輪內側、外側接觸,以此磨削出螺旋傘齒輪凸面與凹面的廓形。因此仿真時,假定螺旋傘齒輪工件保持不動,直口杯砂輪內側及外側以相同軌跡在螺旋傘齒輪凸面及凹面運動,同時繞其軸線高速旋轉,如圖 3 所示。
為了提高仿真精度,采用三維激光掃描顯微鏡 (基恩士 VK-X100)對螺旋傘齒輪曲面進行測量,平行于磨削方向的磨削溝痕為砂輪的相對運動軌跡。選取磨削方向上的一條軌跡線,提取其空間坐標,使用多項式對該軌跡線進行擬合,擬合方程如下所示
根據式(10)可獲得凸面與凹面的螺旋線擬合方程,即為螺旋傘齒輪磨削時齒輪工件的運動軌跡線,亦為仿真時直口杯砂輪的運動軌跡。將式(10)的軌跡擬合方程,通過坐標轉換,得到磨粒磨削螺旋傘齒輪時的運動軌跡。轉換方程如下式所示,x'Gi 、z'Gi 為轉換后磨粒在螺旋傘齒輪工件上磨削坐標。
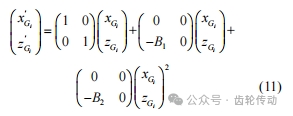
二、砂輪表面形貌特征
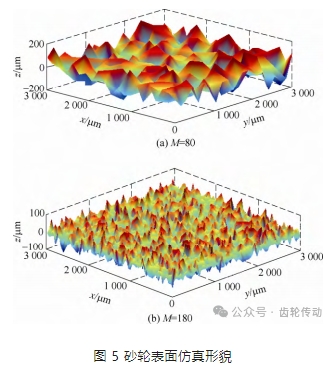
砂輪表面的微觀形貌是影響螺旋傘齒輪磨削過程材料去除的關鍵因素。螺旋傘齒輪工件磨削后表面質量及加工的效率主要取決于磨粒的大小、形狀及分布狀態。圖 4 為使用基恩士激光掃描顯微鏡拍攝的粒度分別為 80 和 180 的 SG 砂輪表面微觀形貌照片。由圖 4 可以看到砂輪表面隨機分布著磨粒,每顆磨粒都具有不規則的大小和形狀,導致與螺旋傘齒輪表面接觸壓力不同,形成不同的切削深度。粒度為 M 的砂輪,其磨粒最大直徑可以表示為
磨粒的平均直徑可以表示為

根據 DOMAN 等提出的磨粒切刃高度服從 (μ,σ2 )正態分布,利用正態分布建立砂輪模型。在建立砂輪模型過程中,假定由砂輪磨粒大小影響并決定磨粒分布狀態,設定切刃的露出高度符合正態分布即 hi 的分布函數如式(14)所示

式中,μ 為正態分布均值,μ=dgavg;σ 為正態分布方差,σ=(dgmax - dgavg)/3;M 為磨粒粒度。
同時假定砂輪表面相鄰磨粒的平均間隔為
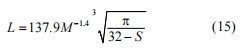
式中,S 為砂輪的結構參數,表示砂輪磨粒的體積含量
式中,Vg 為砂輪的磨粒的體積百分比。
砂輪仿真形貌如圖 5 所示。可以看到,磨粒粒度越大,磨粒的尺寸越小且分布越密。
直口杯砂輪磨削螺旋傘齒輪為成型磨削,砂輪外側與螺旋傘齒輪凹面相切,內側與螺旋傘齒輪凸面相切。通過三維激光掃描顯微鏡對螺旋傘齒輪進行測量,提取垂直磨削方向的凹面和凸面接觸輪廓線,對已建立的砂輪表面廓形進行補償,獲得與實際成型砂輪表面相吻合的砂輪表面形貌仿真模型。
三、螺旋傘齒輪磨削表面形貌仿真
完成直口杯砂輪表面建模仿真后,為了實現螺旋傘齒輪磨削表面形貌仿真,需要對齒面進行離散化處理。齒面采用拓撲矩陣 gmn 來表示,矩陣中每個元素 g(m, n)表示在全局坐標系 oxyz 中齒面 xy 平面中各網格點(m, n)對應的 z 向坐標值,即求解得出的磨削后齒面的殘余高度值。對砂輪表面進行離散化處理,并用拓撲矩陣 hij 表示,其中 h(i, j)表示在砂輪周向和軸向(i, j)位置的磨粒高度。砂輪磨削齒面過程可以看成是由 j 個 xoz 截面上的 i 顆磨粒先后對表面進行刻劃的過程。計算從第 1 個到第 j 個截面上的第 1 個到第 i 顆磨粒的運算軌跡并進行存儲。在工件平面 gmn 上的每一個點 g(m, n)上就對應了若干條軌跡線在該點的值 zi(m, n)。由于磨削為材料去除加工,因此在一個特定的坐標位置上軌跡 z 坐標值最小的磨粒將決定工件最終決定齒面在該點的狀態,則磨削過后最終的齒輪工件表面形貌可表示為殘留在工件表面的軌跡線最低值的集合,即
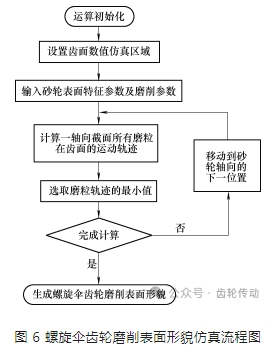
螺旋傘齒輪磨削加工表面形貌仿真過程如下。
(1) 設置磨削參數和砂輪幾何參數,定義工件網格大小,用拓撲矩陣 gmn 表示。工件平面上的每一個點 gij(i=1,2,…,m; j=1,2,…,n)表示工件表面各網格點對應的 z 向高度值。
(2) 將磨粒離散點與矩陣元素對應起來。根據(x, y)與工件高度矩陣 gij 的下標(i, j)的對應關系,判斷磨粒離散點 G 與工件網格點的對應關系。當磨粒離散點 G 的坐標(x, y)剛好落在工件網格點(i, j)上時,就說明該點剛好與矩陣元素 gij 對應,否則,找到(x, y)最接近的工件網格點(i, j),用該網格點所在的矩陣元素 gij 對應此點。
(3) 切削判斷。比較當前時刻選定的磨粒上離散點 G 在工件坐標系中的高度方向坐標值 z 和對應矩陣元素 gij的儲存值。如果 z 小,則說明磨粒已經切入工件,這時用 z 更新 gij 的儲存值。否則不作任何處理。
(4) 根據矩陣 gij 中的寄存數據繪制表面三維形貌圖。螺旋傘齒輪磨削表面形貌仿真流程圖如圖 6 所示。
四、試驗驗證
螺旋傘齒輪磨削試驗結果分析
螺旋傘齒輪磨削試驗在 Gleason-600G 數控磨齒機上進行,采用單因素試驗法,探究磨削速度 vs,展成速度 w 及磨削深度 ap 對齒面粗糙度的影響規律。砂輪采用諾頓直口杯 SG 砂輪,試驗裝置如圖 7 所示。螺旋傘齒輪磨削工藝參數如表 1 所示。加工過程中,每個齒槽分別對應一組參數。磨削加工完成后沿齒輪大端方向向內約 10 mm 深線切下齒樣,并將齒樣在超聲波清洗機中清洗干凈。使用白光干涉儀(CCILITE-M112)測量齒面形貌及粗糙度。

白光干涉儀拍攝的磨削后齒面形貌如圖 8 所示。
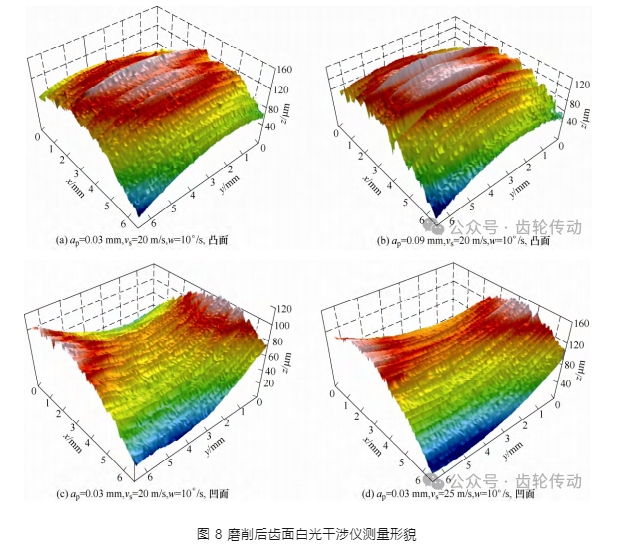
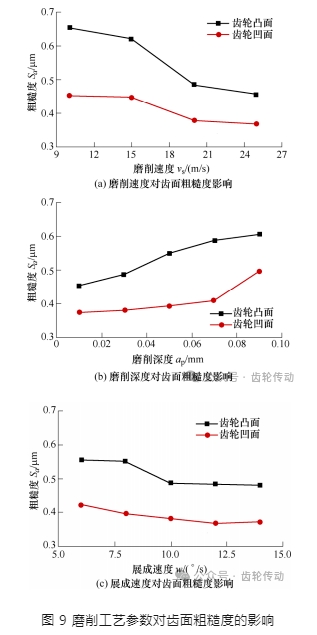
圖 9 為不同磨削參數磨削后齒面粗糙度變化曲線圖。可以看到隨著磨削速度與展成速度的增加,齒面粗糙度皆下降;隨著磨削深度的增加,齒面粗糙度升高。
螺旋傘齒輪磨削仿真結果分析
使用與磨削試驗相同的參數進行仿真,仿真結果如圖 10 所示。將仿真圖 10 與試驗測量圖 8 進行對比,圖 10a、10b 分別為螺旋傘齒輪凹面與凸面的齒面形貌仿真圖,其與圖 8a、8c 試驗后拍攝的齒面形貌總體一致。圖 10a、10d 分別為不同磨削深度磨削后的齒面形貌仿真圖,隨著磨削深度的增大表面劃痕加深,其與圖 8a、8b 試驗后拍攝的工件表面形貌具有一致的規律。圖 10a、10e 分別為不同磨削速度磨削后的齒面形貌仿真圖,隨著磨削速度的增大表面紋理趨于致密,其與圖 8c、8d 試驗后拍攝的工件表面形貌具有一致的規律。
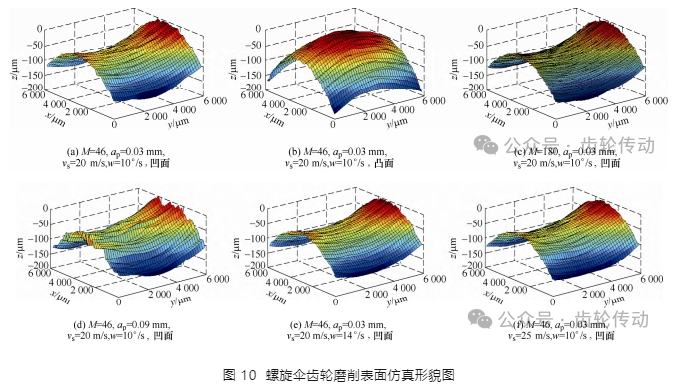
對各螺旋傘齒輪仿真形貌圖進行對比,分析不同工藝參數對螺旋傘齒輪表面形貌的影響原因。對比圖 10a 與 10c 可以看到,砂輪粒度增大,磨粒密度增大,砂輪表面磨粒突出高度減小,磨削時同時參與磨削的磨粒數增加,有利于提高磨削表面質量。對比圖 10a 與 10d 可以看到,磨削深度增加,單顆磨粒未變形切削厚度增大,磨粒對齒面的劃痕加深,使磨削表面質量降低。對比圖 10a 與 10e 可以看到,隨著展成速度的增加,每顆磨粒在齒面刻劃長度增長,相鄰磨粒切削后留下的齒面殘留高度減小,齒面磨削質量有所提高。對比圖 10a 與 10f 可以看到,磨削速度提高單位時間內有效磨粒數增加,隨著每個砂輪磨粒在工件表面上切削次數增多,在多個磨粒累計切削作用下,加工表面殘余高度減小,使得加工表面質量得到提高。
通過對比仿真與試驗的結果,驗證直口杯砂輪磨削螺旋傘齒輪時磨粒運動模型的正確性和有效性。同時說明采用數值仿真的方法可以分析不同磨削參數對螺旋傘齒輪磨削表面形貌的影響規律。在分析某一加工參數對螺旋傘齒輪磨削表面形貌影響時,數值仿真的靈活性可以有效地排除其它干擾因素,準確高效地給出兩者之間的區別。因此,基于螺旋傘齒輪磨削磨粒軌跡建立的表面創成模型可以 用來預測加工表面形貌,并減少試驗次數從而達到廣義的分析效果。
五、結論
(1) 基于正態分布模型和砂輪表面磨粒實際大小,對砂輪表面形貌進行仿真。根據磨削運動學原理,建立了螺旋傘齒輪磨削磨粒切削運動模型。并選擇有效磨粒與工件的干涉痕跡,生成了工件表面的三維數值形貌。
(2) 仿真與試驗所得工件表面微觀形貌特征基本一致,驗證了提出的磨削表面生成算法的正確性和有效性。綜合試驗與仿真結果可知提高磨削速度與展成速度、增加磨粒粒度皆有利于獲得良好的磨削表面形貌。
(3) 該模型可以生成不同工藝參數的螺旋傘齒輪磨削表面形貌,并可用于分析螺旋傘齒輪磨削表面形貌的產生過程及各加工參數對其影響機理。
參考文獻略.
