航空領域中,齒輪傳動因具備平穩、效率高等優勢被大量使用。航空齒輪多采用成型磨削來提高齒面性能,磨削時砂輪與齒輪表面緊密貼合,切削液難以完全進入磨削區域,易發生齒面燒傷,在高速重載的工況下導致微裂紋擴展,甚至導致材料脫落,影響航空產品的整體性能。
齒輪磨削過程中伴隨著變形、斷裂以及熱量傳遞,是典型的熱-力耦合問題,采用試驗法研究磨削燒傷問題存在周期長、成本高等缺點。數字仿真技術的發展,為齒輪磨削燒傷問題的研究提供了方向。J. S. Strenkowski 利用有限元 法研究了齒輪磨削時的平面應變和等效塑性應變對切屑分離的影響。T.Ozel 等學者根據應變、應力等系數,利用有限元方法,實現了磨削時樣件的流動應力公式的求解。楊祎旭建立了單顆磨粒磨削加工的有限元模型,研究了工藝參數與應力、應變以及溫度場間的關系。周靜等利用有限元分析軟件對螺旋錐齒輪進行了建模,并開展了力-熱耦合仿真分析。
上述有限元仿真研究多圍繞單磨粒為磨削主體開展,實際磨削過程中,砂輪表面參與磨削的磨粒眾多,且呈現隨機分布的特點,傳統的仿真方法降低了仿真結果的可信度。鑒于此,本文開展了多磨粒砂輪-齒輪的磨削仿真,以 Gr10CrNi3Mo 材料為研究對象,研究了磨削參數對磨削溫度場的影響規律,通過開展齒輪磨削試驗,驗證仿真模型的合理性;利用 BP 神經網絡建立磨削燒傷預測模型,降低磨削燒傷發生的機率。
一、仿真模型建立
利用有限元分析軟件 ABAQUS,完成工件-砂輪模型、材料參數設置、邊界條件設置,建立磨削仿真模型,具體步驟如下。
物理模型
(1)工件模型
磨削溫度場由瞬態到穩態的時間極短,熱量來不及繼續傳遞就會被冷卻液帶走,沿磨削深度方向的傳播距離有限。考慮到齒輪尺寸遠大于磨粒的尺寸,可近似認為磨粒在磨削時作平面運動。設工件為長方體,尺寸 1.75mm×1.6mm×0.25mm,工件模型如圖 1 所示。

(2)多磨粒砂輪模型
在磨削加工過程中,參與磨削的磨粒呈現隨機分布的特點。參考相關文獻,建立隨機分布的多磨粒砂輪模型,如圖 2 所示。
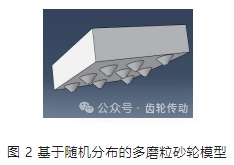
材料參數
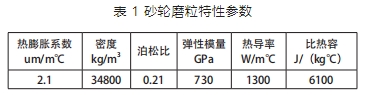
選取砂輪型號 32GC120 - J8BL。砂輪磨粒的主要參數如表 1 所示。
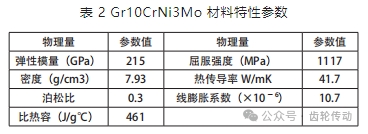
工件材料選擇 Gr10CrNi3Mo,材料特性參數見表 2。
邊界條件
磨削過程屬于高度非線性問題,選擇動態-顯式時間積分更適合于求解動態接觸斷裂問題。
邊界條件設置:定義砂輪為主動件,工件為從動件,摩擦系數設置為 0.2;選擇水基冷卻液,在模型中設置對流換熱系數為 0.49W/mm2℃;選擇順磨加工,砂輪線速度范圍為 20m/s~30m/s,磨削深度范圍 0.01mm~0.1mm,忽略橫向進給速度的影響。將磨削路徑上沿著磨削深度方向 0.1mm 內的網格細化,其余網格適當粗化處理,如圖 3 所示。

二、仿真結果分析
磨削燒傷的根本原因在于瞬時溫升過高,本文以磨削過程中齒面的瞬時最高溫度為研究對象,開展磨削參數對齒面磨削溫度場的影響規律分析。
砂輪線速度對磨削溫度場的影響
圖4 顯示了不同砂輪線速度下的齒面溫度分布云圖(磨削深度 ap=0.01mm)。
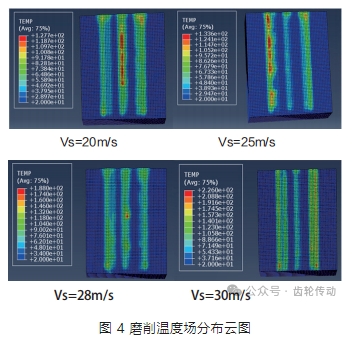
隨著砂輪線速度的提高,齒面瞬時最高溫度呈現上升的趨勢。磨粒可等效為以恒定速度在齒面上運動的熱源,當砂輪線速度提高時,耕犁及滑擦作用的磨粒數增多,磨削產生的熱量增加,導致齒面溫度上升。
磨削深度對磨削溫度場的影響
圖 5 顯示了不同磨削深度下的齒面溫度分布云圖(砂輪線速度 Vs=25m/s)。

隨著磨削深度的增加,齒面瞬時最高溫度呈現上升的趨勢。增大磨削深度后,磨削過程中去除的材料體積增加,磨削過程中的磨屑變形和摩擦力增加,需要消耗更多的能量來克服摩擦功和材料的變形功,導致齒面溫度大幅度提高。
三、成型磨削試驗
為驗證上述有限元模型及結論,本文開展了齒輪磨削加工試驗。
試驗樣件及設備
① 機床:平面磨床 ② 砂輪:P20*2.2*4.0,32GC120 - J8BL ③ 工件材料:Gr10CrNi3Mo,尺寸:60mm(長)×40mm(寬)×30mm(高)④ 磨削用量:砂輪線速度 Vs=20m/s ~ 28m /s,橫向進給速度 Vw= 25mm/s,磨削深度 ap=0.01mm ~ 0.05mm;磨削余量 0.05mm ⑤冷卻液:5%乳化液⑥磨削方式:順磨⑦修整工具:金剛石滾輪;修整深度d =0.01mm,軸向進給速度 Vd=20mm/min,修整速比a =0.5。
在試件上采用線切割的方法加工齒槽,如圖 6 所示。

試驗方案設計
(1)磨削參數選擇
以砂輪線速度和磨削深度為變量,建立磨削加工試驗方案,如表 3 所示。
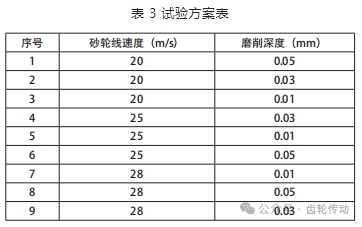
(2)磨削溫度測量
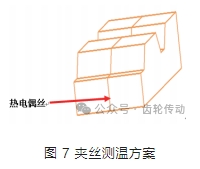
①采用圖 7 所示的夾絲測溫方法,將熱電偶絲貼在齒根處,利用溫度測量表測量該處的溫度,記錄每組試驗的瞬時最高溫度。
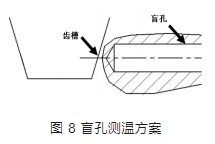
②采用圖 8 所示的溫度測量方案,獲取齒面沿齒厚方向溫度分布。在距離齒槽 1mm ~ 2mm 處加工? 2 的盲孔,將熱電偶絲埋入盲孔,端頭與孔底接觸,用密封膠將端口封好。每次磨削后計算齒面與孔底之間的距離,同時記錄磨削溫度,得到同一組磨削參數下沿齒厚方向的溫度分布情況。
試驗結果分析
(1)齒面瞬時最高溫度
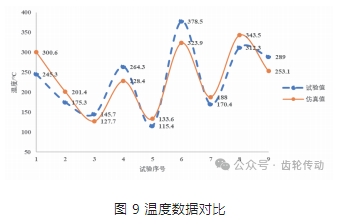
圖 9 顯示了齒面瞬時最高溫度的試驗數據與仿真數據的對比情況。在齒面溫度隨磨削參數的變化趨勢上,試驗數據與仿真數據是相同的,最大相對誤差 22.5%,其余各組偏差在 10%~16% 之間,出現偏差的原因主要有以下兩方面:
①磨削溫度的測量精度受客觀條件制約。熱電偶絲與齒面的距離難以精確控制、熱電偶絲響應時間,都可能影響溫度數據的測量。
②仿真模型的邊界條件設置與簡化假設。工件、砂輪材料參數、對流換熱系數等與實際情況存在偏差;由于磨粒形狀、磨粒在結合劑上的位姿等均作了簡化處理,也可能對計算結果造成影響。
(2)沿齒厚方向溫度分布情況
取砂輪線速度 25m/s,磨削深度 0.01mm,進給速度 25mm/s。設計盲孔底部與齒面的距離為 1mm。盲孔加工完成后,首先進行 4 次快速磨削,去除 0.04mm 的余量,使盲孔底部與齒面距離為 0.06mm。待試件完全冷卻后,進行 5 次磨削加工,每次去除 0.01mm 的余量。
從圖 10 可以看到,試驗數據與仿真數據在沿齒厚方向的變化趨勢是相同的,試驗數據略大于仿真數據,最大偏差為 9℃,在可接受范圍內。

上述分析在一定程度上驗證了所建立的有限元仿真模型的合理性,考慮實際加工中的各種影響因素,仿真數據與試驗數據之間的偏差是難以避免的,可借鑒仿真分析來模擬實際磨削過程,降低加工風險。
四、基于 BP 神經網絡的磨削燒傷預測
磨削燒傷影響齒輪的使用性能,如何實現磨削燒傷的有效預測,是人們一直研究的問題。人工神經網絡為解決上述問題提供了思路。人工神經網絡通過數量眾多的神經元進行信息的傳遞與處理,具有強大的自學習特性,適用于處理復雜的非線性問題。本文利用 BP 神經網絡建立齒輪磨削燒傷預測模型,實現磨削燒傷的有效預測。
BP 神經網絡工作原理
圖 11 表示了神經元的工作原理。其中 X1 ~ Xn 是從神經元 j 輸入到神經元 i 的信號,Wi1 ~ Win 表示對應的連接權值,yi 表示神經元i的輸出。
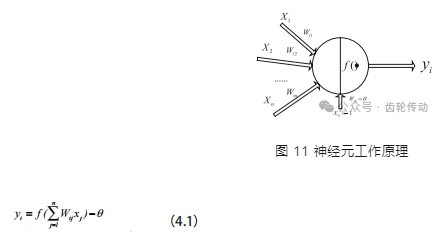
式中:θ 表示閾值,當外界刺激大于該神經元的閾值時,神經元會被激活;f 為神經元功能函數。常采用雙極 Sigmoid 函數,函數形式為:
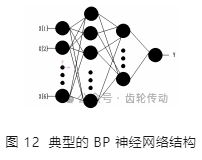
BP 神經網絡由多個層級組成,分為輸入層、隱層和輸出層,圖 12 是一種典型的 BP 神經網絡結構。其工作原理為:樣本數據經過輸入層和隱層之間的計算和處理,由輸出層輸出。若輸出層的實際輸出與期望輸出存在誤差,誤差將會以某種形式通過隱層向輸入層逐層反轉,并修正連接權值和閾值;當神經網絡的輸出誤差減少到預先設定的數值時,訓練停止。當設定的誤差值足夠小,且訓練樣本足夠多時,利用 BP 神經網絡建立的模型精度就越高,預測的準確性就越高。
神經網絡模型建立
設模型的輸入矢量為多維矢量,輸出矢量為一維矢量。對于磨削加工,輸入矢量表示磨削材料、磨削參數、切削液種類等因素,輸出矢量可表示材料的燒傷結果。磨削燒傷的輸入、輸出關系復雜,為提高神經網絡計算的準確性,設置網絡隱層的數量為兩層,神經元個數分別為 9 個和 5 個。輸入矢量為六維,即神經網絡的結構為 6-9-5-1。
神經網絡的輸入向量 X 可由下式表示:
X=[X1,X2,X3,X4,X5,X6] (4.3)
式中,X1 ~ X6 分別表示工件材料、砂輪種類、磨削液種類、砂輪線速度(m/s)、進給速度(mm/s)、磨削深度(mm)。
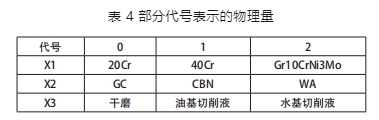
如樣本矢量 [0,2,2,35.0,30.0,0.05,1] 表示工件材料為 20Cr,砂輪材料 WA,水基切削液,砂輪線速度 35m/s,進給速度 30mm/s, 磨削深度 0.05mm,發生了磨削燒傷。
本文利用 MATLAB,實現基于 BP 神經網絡的燒傷預測,流程如圖 13 所示。
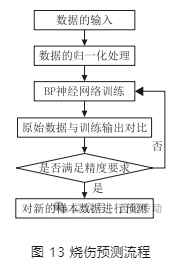
(1)數據的歸一化:對進行數據的歸一化處理的目的在于:減小數據范圍,縮短訓練時間。選用雙極 Sigmoid 函數作為神經網絡的激活函數,將輸入、輸出數據歸一到 [-1,1] 區間;
(2)BP 神經網絡訓練:利用 MATLAB 神經網絡工具箱創建神經網絡,采用梯度下降自適應學習率訓練函數,設置訓練參數;
(3)原始數據與訓練輸出數據對比:利用神經網絡訓練樣本數據,將訓練結果還原為原始數據級,并于原始數據進行對比,驗證模型精度;
(4)在神經網絡模型的計算精度滿足設計要求的前提下,輸入新的樣本數據,實現磨削燒傷預測。
磨削燒傷預測
BP 神經網絡的訓練需要大量的樣本數據。從降低人力、物力的角度出發,可近似由磨削仿真分析結果來代替,并假設當表面瞬時最高溫度達到 440℃時發生磨削燒傷。通過磨削仿真得到 45 組樣本數據,部分數據如表 5 所示(最后一列“0”代表無燒傷,“1”表示燒傷):
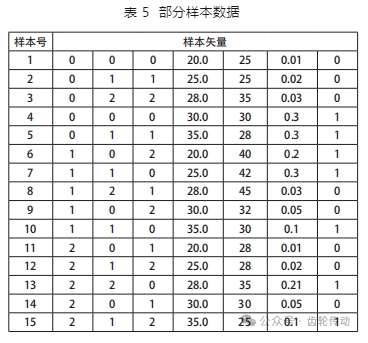
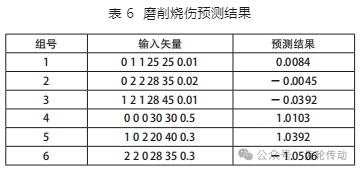
將表 6 中的 1~3 組樣本數據輸入到模型中,輸出矢量為 0.0084,-0.0045,-0.0392,顯示未發生磨削燒傷。由于這 3 組樣本與表 5 未發生燒傷的第 2、3、8 號樣本對比,僅磨削深度變小,從前文仿真分析可知,磨削深度越小,齒面溫度越低,說明神經網絡的預測結果是正確的。
將表 6 的 4-6 組樣本數據輸入到模型中,輸出矢量為 1.0103、1.0392、-1.0506,顯示發生了燒傷。表 5 發生磨削燒傷的第 4、6、13 號樣本,其磨削深度值小于表 6 中 的第 4、5、6 號樣本,因此表 6 中的第 4、5、6 號樣本也必然發生磨削燒傷,說明神經網絡的預測結果是合理的。
五、結語
本文針對 Gr10CrNi3Mo 材料,開展了基于多磨粒磨削的有限元仿真,對磨削參數與磨削溫度場之間的關系進行了研究,開展了齒輪成型磨削試驗,通過比較實際磨削過程與仿真過程的溫度數據,驗證了仿真分析的合理性,利用 BP 神經網絡,建立了磨削燒傷預測模型,利用樣本數據對模型進行了訓練,提高了模型的計算精度,實現了航空齒輪的磨削燒傷預測。本文的研究成果有助于提高磨削仿真分析的準確性,提出的 BP 神經網絡可在開展實際磨削加工前預測磨削燒傷,便于合理選擇磨削參數,降低燒傷概率。
參考文獻略.
