精密減速器是高精度衛(wèi)星天線、機(jī)器人及精密機(jī)床等設(shè)備中的核心零部件。目前,國內(nèi)精密減速器存在傳動(dòng)精度低、承載能力不足等問題,高質(zhì)量的精密減速器主要依賴進(jìn)口,影響了國產(chǎn)精密減速器的發(fā)展。擺線輪是精密減速器傳動(dòng)系統(tǒng)的核心零件,存在加工齒廓偏離理論設(shè)計(jì)齒廓程度較大的問題,且缺乏專用的擺線輪加工精度測量設(shè)備,因此無法對(duì)制造誤差進(jìn)行預(yù)控,這是影響精密減速器承載能力和嚙合傳動(dòng)精度的核心問題。

　　隨著科技的快速發(fā)展,對(duì)精密減速器品質(zhì)和性能的要求越來越高,因此,擺線輪的加工制造精度問題日益凸顯。從擺線輪誤差測量方面來看, 傳統(tǒng)的測量方法,如頂根距、雙量棒、外公法線等, 只限于對(duì)齒輪上的特殊點(diǎn)進(jìn)行檢測,難以反映擺線輪整體的誤差情況,更難以保證擺線輪高精度加工的穩(wěn)定性。文獻(xiàn)采用極坐標(biāo)測量方法完成相應(yīng)測量儀器的開發(fā),但并沒有投入使用。此外,擺線輪的制造誤差可以采用三坐標(biāo)測量儀準(zhǔn)確獲取,但需要配套的驅(qū)動(dòng)程序,成本高,難以精確控制數(shù)據(jù)處理過程,至今未得到廣泛應(yīng)用。以上方法可對(duì)擺線輪的高精測量提供借鑒和參考。

　　胡文石通過對(duì)擺線輪的空位置度、孔內(nèi)徑和圓度等關(guān)鍵技術(shù)的研究,實(shí)現(xiàn)了擺線輪的誤差檢測,在一定程度上提高了精密減速器的裝配精度。孫彬等和李兵等采用接觸式電感傳感器完成了擺線輪測量系統(tǒng)的開發(fā)以及關(guān)鍵尺寸的檢測,實(shí)現(xiàn)了擺線輪加工誤差的測量與評(píng)定。Fang等通過分析擺線輪在測量過程中影響測量精度的因素,完成了齒面數(shù)學(xué)模型的構(gòu)建,并設(shè)計(jì)了擺線輪在測量過程中軸線對(duì)角度誤差的補(bǔ)償方法,提高了擺線輪的測量精度。上述方法均可實(shí)現(xiàn)擺線輪齒廓誤差的高精度檢測,但獲取擺線輪制造誤差的整個(gè)過程均基于三維測頭的齒輪測量中心,三維測頭價(jià)格不僅昂貴,而且關(guān)鍵技術(shù)進(jìn)行知識(shí)產(chǎn)權(quán)保護(hù),不利于與國內(nèi)加工機(jī)床形成閉環(huán)。近年來,一維測頭測量技術(shù)及應(yīng)用快速發(fā)展, 已掌握測量路徑規(guī)劃和數(shù)據(jù)補(bǔ)償?shù)汝P(guān)鍵技術(shù),能夠準(zhǔn)確完成錐齒輪等復(fù)雜齒面的誤差檢測,測量精度與重復(fù)性能滿足工程需求。此外,一維測頭價(jià)格低廉,運(yùn)動(dòng)控制相對(duì)容易,且可與國內(nèi)齒輪加工機(jī)床形成閉環(huán)聯(lián)系,已成為齒輪加工企業(yè)進(jìn)行擺線輪精度控制的重要設(shè)備。Dai等和 Li 等使用一維測頭準(zhǔn)確完成了錐齒輪復(fù)雜型面的齒面偏差測量與評(píng)定。因此,通過基于一維測頭的齒輪測量中心代替基于三維測頭的齒輪測量中心能夠探明擺線輪的精密測量處理過程、方法以及制造誤差補(bǔ)償?shù)燃夹g(shù),進(jìn)而可以準(zhǔn)確且快速的獲知其制造誤差。這不僅可以對(duì)擺線輪加工 質(zhì)量進(jìn)行有效檢測和評(píng)定,而且對(duì)其它相關(guān)零部件制造誤差的準(zhǔn)確控制十分重要。

　　鑒于此,本文基于國產(chǎn)的JB45型齒輪測量中心提出了一種基于一維測頭的擺線輪制造誤差數(shù)字化測量方法。根據(jù)擺線輪成形和測量模型,計(jì)算齒廓測量所必需的理論數(shù)據(jù),基于測頭的實(shí)際運(yùn)動(dòng)軌跡數(shù)據(jù),深入分析擺線輪制造誤差計(jì)算過程與方法、構(gòu)建誤差模型,進(jìn)而獲取擺線輪的實(shí)際制造誤差。通過國產(chǎn)齒輪測量中心的檢測結(jié)果驗(yàn)證了所提出測量理論和處理方法的正確性。

　　一、實(shí)際齒廓的數(shù)字化檢測

　　理論齒廓是檢測擺線輪制造誤差的基準(zhǔn)齒廓, 不僅可以通過與理論齒廓的對(duì)比,評(píng)估實(shí)際齒廓的偏差,從而確保傳動(dòng)比的精確性,而且理論齒廓提供了測量基準(zhǔn),幫助確定擺線輪在齒輪測量中心上的正確位置,從而保證測量結(jié)果的準(zhǔn)確性。因此, 完成理論齒廓的構(gòu)建對(duì)于擺線輪的準(zhǔn)確測量尤為重要。文獻(xiàn)對(duì)其進(jìn)行了詳細(xì)的論述。理論齒廓及其法矢可表達(dá)為

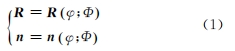
　　式中:φ為輪齒轉(zhuǎn)角(范圍為0~360°);Φ 為擺線輪加工參數(shù)集合。

　　根據(jù)精密檢測原理可知,測頭是半徑為r的測球,會(huì)對(duì)擺線輪的測量過程造成一定影響。綜合考慮到測頭半徑r的影響,齒廓檢測得到的是測球球心的運(yùn)動(dòng)坐標(biāo)。根據(jù)測頭半徑補(bǔ)償原理可得工件坐標(biāo)系S_W 下測球的理論運(yùn)動(dòng)軌跡R_e

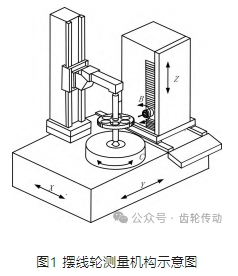
　　在測量過程中,齒輪測量中心采用坐標(biāo)測量原理,測頭首先運(yùn)動(dòng)至被測齒坯的某一齒廓參考點(diǎn)的理論位置,然后測量中心回轉(zhuǎn)工作臺(tái)自動(dòng)旋轉(zhuǎn)使得擺線輪完成被測齒廓的靠齒動(dòng)作。之后,計(jì)算機(jī)根據(jù)擺線輪被測齒廓的理論數(shù)據(jù)控制直線軸Y 和旋轉(zhuǎn)軸C 的插補(bǔ)運(yùn)動(dòng)。各坐標(biāo)軸運(yùn)動(dòng)過程中,測頭始終與齒廓保持接觸(測頭電感部分需增設(shè)隨動(dòng)跟蹤機(jī)構(gòu)),計(jì)算機(jī)連續(xù)采集各接觸點(diǎn)的實(shí)際坐標(biāo)值,并存儲(chǔ)起來,直至擺線輪繞中心軸連續(xù)轉(zhuǎn)動(dòng)旋轉(zhuǎn)一周或完成單個(gè)齒廓的測量,則檢測結(jié)束。通過實(shí)際齒廓與理論齒廓的比較處理后即可計(jì)算得到擺線輪實(shí)際齒廓的制造誤差。因此,為準(zhǔn)確明晰擺線輪制造誤差的獲取過程,建立圖1所示的擺線輪實(shí)際齒廓檢測數(shù)學(xué)模型(由三個(gè)直線軸 X、Y、Z 和兩個(gè)旋轉(zhuǎn)軸B、C 組成)。

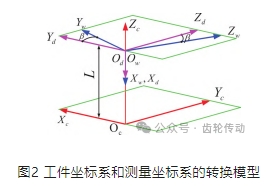
　　由圖1可建立圖2所示的工件坐標(biāo)系和測量坐標(biāo)系的轉(zhuǎn)換關(guān)系模型。工件坐標(biāo)系 S_W (X_W ,Y_W ,Z_W ) 和測量坐標(biāo)系S_C (X_C,Y_C,Z_C ) 分別固連于輪坯和齒輪測量中心,O_C 為旋轉(zhuǎn)工作臺(tái)的中心。S_d (X_d,Y_d,Z_d ) 為輔助坐標(biāo)系。直線位移量 L 用于被測輪坯定位,由測球高度確定;β為 S_W 與 S_C 間的轉(zhuǎn)角偏移量,其確定因素包括測球位置和被測齒廓,用于獲取被測齒廓位置。

　　在實(shí)際測量過程中,需要將被測擺線輪的工件坐標(biāo)系轉(zhuǎn)換至測量坐標(biāo)系中進(jìn)行測量,即將輪坯由工件坐標(biāo)系S_W 向測量坐標(biāo)系S_C 進(jìn)行空間變換,得

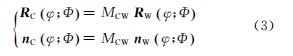
　　式中,

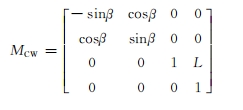
　　輪坯位移量L 確定后,由于仍存在回轉(zhuǎn)自由度 (β,圖1),因此,需要確定實(shí)際齒廓與理論齒廓在坐標(biāo)系S_C 中的相對(duì)位置關(guān)系,即確定實(shí)際齒廓上測量參考點(diǎn)K 的位置(圖3)。測量參考點(diǎn)是測量起始點(diǎn),通常可以選擇齒頂、齒根和節(jié)點(diǎn)位置,并認(rèn)為理論齒廓和實(shí)際加工齒廓在該測量參考點(diǎn)處的制造誤差為0,剩余點(diǎn)的制造誤差可根據(jù)測量點(diǎn)與參考點(diǎn)的相對(duì)位置得到。

　　通常在齒頂和齒根位置修形量較大,以便于儲(chǔ)存潤滑油和裝配,但不參與輪齒的嚙合傳動(dòng),不宜參與輪齒定位;而在節(jié)點(diǎn)位置的修形量極小,位于輪齒接觸的主要齒廓段中,可保證嚙合齒廓具有良好的嚙合傳動(dòng),利于被測齒廓定位,因此,選擇齒廓節(jié)點(diǎn)作為測量參考點(diǎn)進(jìn)行被測齒廓定位。

　　為準(zhǔn)確獲取擺線輪齒廓的制造誤差,測頭首先在參考點(diǎn)接觸,然后對(duì)整個(gè)齒廓進(jìn)行檢測,并對(duì)測量結(jié)果進(jìn)行處理即可。

　　二、實(shí)際齒廓的誤差計(jì)算

　　由于基于齒輪測量中心完成齒廓測量后獲取的僅僅是離散齒廓坐標(biāo)點(diǎn),無法直接根據(jù)離散齒廓坐標(biāo)點(diǎn)完成實(shí)際齒廓誤差計(jì)算,需采用擬合算法對(duì)離散坐標(biāo)點(diǎn)進(jìn)行曲線擬合,進(jìn)而完成實(shí)際齒廓誤差計(jì)算。非均勻有理 B 樣條(Non-Uniform Rational B-spline,NURBS)法廣泛用于計(jì)算機(jī)圖形學(xué)中。在工程領(lǐng)域,NURBS法在 CAD/CAM 中有強(qiáng)大的造型功能,因而被各類主流的幾何造型系統(tǒng)作為曲線曲面唯一的表示方法。在實(shí)際應(yīng)用中,它能夠精確表示二次、三次 NURBS 曲線曲面。NURBS 能夠精確、靈活地描述復(fù)雜的二維和三維幾何形狀, 從而在產(chǎn)品設(shè)計(jì)、制造等領(lǐng)域發(fā)揮重要作用。因 此,采用 NURBS算法完成實(shí)際齒廓的擬合,并在此基礎(chǔ)上進(jìn)行后續(xù)分析。

　　定義沿著理論齒廓R 被測點(diǎn)處的法線方向n, 實(shí)際齒廓R^* 與理論齒廓R 的法向距離為齒廓誤差 δ ,如圖4所示。沿著法矢n的方向,過齒廓R 上一點(diǎn)P0 ,交齒廓R^* 上與點(diǎn)P₀ 相對(duì)應(yīng)的點(diǎn)P^* ,P₀P^* 為這兩點(diǎn)間的齒廓偏差δδ 的幾何描述。

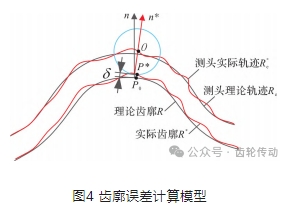
　　理論齒面上每一點(diǎn)都對(duì)應(yīng)唯一δ,所以可以認(rèn)為δ與曲線坐標(biāo)φ 有關(guān),且由式(1)可確定Φ 是φ 的參變量。則齒廓誤差可表示為

　　則,可得測頭實(shí)際運(yùn)動(dòng)軌跡R^*_e 為

　　式中,n^* 為實(shí)際齒廓R^* 的法矢。

　　值得注意的是,在擺線輪的測量過程中,實(shí)際齒廓與理論齒廓的相對(duì)位置不是完全貼合的,為減小或消除測量基準(zhǔn)不重合誤差及齒距誤差,對(duì)于擺線輪這種回轉(zhuǎn)體零件來說,需要實(shí)際齒廓向理論齒廓作最佳匹配處理,進(jìn)而使得實(shí)際齒廓與理論齒廓完全貼合。以測量所得的離散測量數(shù)據(jù)點(diǎn)上的齒廓誤差平方和最小為目標(biāo)函數(shù),以 X、Y 軸的移動(dòng)量 Δx 和Δy ,Z 軸的轉(zhuǎn)動(dòng)量Δz 為設(shè)計(jì)變量,通過單純形法等數(shù)值迭代方法尋求移動(dòng)量和轉(zhuǎn)動(dòng)量的最優(yōu)值。建立曲線匹配模型為

　　式中:n 為被測點(diǎn)的個(gè)數(shù);D 為被測點(diǎn)間的法向距離。采用單純形法對(duì)式(6)進(jìn)行求解。

　　實(shí)際齒廓與理論齒面最佳匹配后,曲線形狀并未發(fā)生變化,將匹配后的R^*_e與R_e作比較,得

　　將式(4)代入(7),根據(jù)微分幾何原理得

　　測頭半徑r和參數(shù)Φ 已知,測頭實(shí)際軌跡 R^*_e 由 NURBS重構(gòu)確定,理論齒面R 和法矢n 由式(1) 得到。因此,式(10)是一個(gè)以δ和φ 為變量的非線性方程組,由牛頓-拉菲森算法求解可得到相應(yīng)的齒廓制造誤差。

　　三、實(shí)驗(yàn)驗(yàn)證

　　以國產(chǎn)的JB45型齒輪測量中心和1700RV 減速器中的擺線輪來驗(yàn)證文中理論和方法的正確性。表1所示為被測輪齒的幾何參數(shù)。在工件坐標(biāo)系下,以等轉(zhuǎn)角φ的方式在被測齒廓上選擇3600個(gè)點(diǎn),并進(jìn)行相應(yīng)的數(shù)字化處理。實(shí)驗(yàn)中對(duì)某單一齒廓進(jìn)行檢測,表2所示為工件坐標(biāo)系下單一齒廓主要被測點(diǎn)的理論位置坐標(biāo)和法線方向坐標(biāo)。

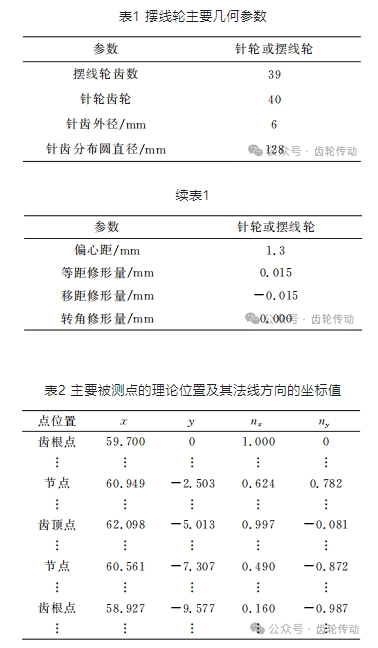
　　選取直徑為2mm 的測頭,并根據(jù)式(2)獲取工件坐標(biāo)系下的測頭中心理論運(yùn)動(dòng)軌跡后,由式(3) 可將理論坐標(biāo)和法矢轉(zhuǎn)至測量坐標(biāo)系下。將擺線輪安裝于圖5所示的JB45型齒輪測量中心上,在測頭接觸測量參考點(diǎn)后即可確定被測齒廓位置,并根據(jù)測量參考點(diǎn)位置完成測頭的靠齒定位動(dòng)作。采用點(diǎn)陣式測量方法對(duì)被測點(diǎn)進(jìn)行檢測,由此獲取測球中心的實(shí)際運(yùn)動(dòng)軌跡坐標(biāo)。對(duì)測球中心檢測數(shù)據(jù)進(jìn)行半徑反補(bǔ)償處理,由此獲取實(shí)際齒廓坐標(biāo)值。

　　基于測量坐標(biāo)系下的擺線輪齒廓離散坐標(biāo)值和 NURBS算法完成對(duì)實(shí)際齒廓進(jìn)行擬合,擬合的最大誤差為9.5×10^-10 mm,滿足要求。齒廓R^* 與齒廓R 匹配時(shí),轉(zhuǎn)換矩陣中的輪坯最佳轉(zhuǎn)動(dòng)量為 0.003°,最佳移動(dòng)量Δx =3.6mm,Δy =1.5mm,目標(biāo)值F_min =2.7856。檢測時(shí),芯軸定位精度在2 mm 以內(nèi),所以齒廓最佳匹配修正量和目標(biāo)函數(shù)值減小量較小。

　　齒廓誤差精確計(jì)算后得到該擺線輪的齒廓誤差和齒距誤差,如圖6和7所示。

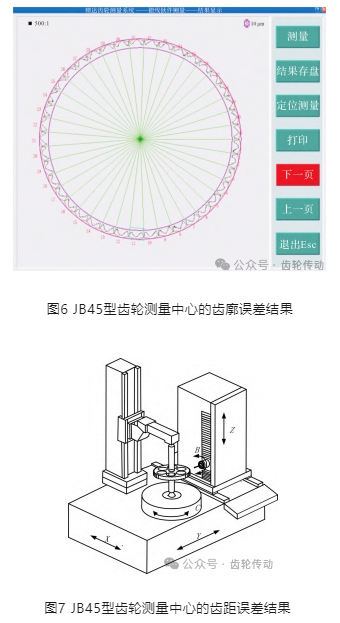
　　圖6中,該擺線輪的最大齒廓誤差為89.4 mm, 平均齒廓誤差為88.9 mm;圖7中,徑向跳動(dòng)、齒距偏差、齒距累積偏差和頂根距變化量的具體值分別為9.2、6.1、27.6和19.2 mm,符合實(shí)際齒形公差和齒距公差的要求。

　　由上述實(shí)驗(yàn)驗(yàn)證結(jié)果可知,文中所提出的擺線輪制造誤差數(shù)字化檢測理論和方法在國產(chǎn)測量中心上的結(jié)果準(zhǔn)確、高效。

　　四、結(jié)論

　　基于一維測頭的齒輪測量中心提出了一種精密減速器擺線輪制造誤差的數(shù)字化測量方法,并在國產(chǎn)JB45型齒輪測量中心上對(duì)該方法進(jìn)行驗(yàn)證。結(jié)果表明:精密減速器擺線輪制造誤差檢測軟件系統(tǒng)的實(shí)際應(yīng)用驗(yàn)證了該理論方法的實(shí)用性;該數(shù)字化測量方法,不僅拓展了齒輪測量中心的功能,而且能夠快速而準(zhǔn)確的測量和評(píng)價(jià)擺線輪的制造誤差,從而可為國內(nèi)精密減速器擺線輪制造精度的評(píng)價(jià)、監(jiān)控和改善提供技術(shù)支持。

　　參考文獻(xiàn)略.