相較于插齒、銑齒等傳統內齒輪加工方法,車齒具有材料去除率高、成形精度好等優點,同時具備實現精加工的潛能,可以進一步縮短加工鏈,降低能耗。但車齒由于獨特的加工特性,成形齒面會呈現出波紋狀的進給刀痕,影響齒面質量,阻礙了其精加工應用。因此,研究車齒加工誤差影響因素,降低成形齒面波紋誤差是推廣車齒工藝發展,實現齒輪高效加工的關鍵。
目前,國內外學者對車齒工藝進行了大量研究,并且在車齒工藝原理、刀具設計、切屑成形機理、加工誤差等方面取得了一定成果。針對車齒加工精度的問題,Guo研究了刀具運動偏心誤差對車齒加工精度的影響,研究結果表明工件齒面出現的進給刀痕的切深與刀具的運動偏心有關,進而在較大程度上影響著工件的齒向和齒形誤差。Maximilian提出了一種計算車齒成形齒面微觀形貌的數學模型,并基于該模型探討了不同軸向進對齒面微觀形貌的影響規律以及對齒輪噪聲的影響。吳震宇針對軸交角誤差的存在影響車齒精度的問題,詳細對比分析了無進給、刀具進給和工件進給三種不同進給方式以及不同軸交角誤差方向對車齒加工誤差的影響程度。楊亞蒙根據車齒運動學原理建立了機床幾何位姿誤差與車齒成形齒面法向誤差的映射關系,研究了各項幾何位姿誤差對法向誤差的影響程度。
本文采用數值仿真的方法建立了齒面誤差模型,首先基于車齒工藝理論和齊次坐標變換原理,根據刀具和工件的運動學關系建立了刀具切削刃空間軌跡曲面幾何數學模型;然后采用離散網格方法計算得到齒面法向誤差形貌;最后分析了軸向進給量、刀具前角、刀具螺旋角對最大齒面偏差的影響程度。該模型可以為車齒工藝參數優化、刀具幾何設計等研究提供支撐。
一、車齒工藝原理
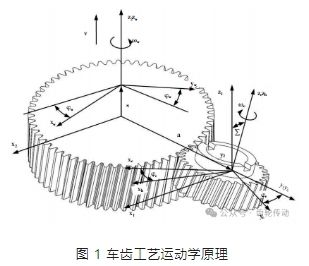
加工外齒輪時車齒刀與工件的相對位置與運動關系如圖 1 所示。車齒工藝的五個切削參數對應機床的五種運動:車齒刀的回轉運動是車齒加工中的主運動,在車齒加工過程中車齒刀以恒定轉速 ωc(rad/min)繞軸線連續回轉;工作與車齒刀按照一定的傳動比關系同步回轉以保證兩者正確嚙合從而獲得正確的齒形,在車齒加工過程中工件以恒定轉速 ωw(rad/min)繞軸線連續回轉;工件沿軸線軸向進給加工出齒輪齒寬,描述軸向進給運動的參數為 v(mm/min);安裝中心距 a 由機床切削運動調整決定;為了保證車齒刀與工件在節圓柱面上的螺旋線相切,需要將車齒刀的軸線相對于工件端面偏轉一個角度 Σ 進行交錯安裝。
安裝中心距 a 的大小由車齒刀分度圓半徑 rc 與工件分度圓半徑 rw 決定:
式中:“+”用于外齒輪嚙合車齒加工;“-”用于內齒輪嚙合車齒加工。本文建立的模型為車齒加工外齒輪模型,此時安裝中心距 a 的大小為 rc+rw。
車齒刀與工件軸線之間的傾斜角被成為軸交角,軸交角 Σ 與車齒刀分度圓螺旋角 βc 和工件分度圓螺旋角 βw 有關,三者關系為:
式中:當加工外齒輪時,“+”用于車齒刀和工件的螺旋方向一致,“-”用于車齒刀和工件的螺旋方向相反;當加工內齒輪時,“+”用于車齒刀和工件的螺旋方向相反,“-”用于車齒刀和工件的螺旋方向一致。本文模型中車齒刀和工件均為右旋,因此軸交角 Σ 的大小為 βc+βw。
在實際車齒加工過程中,軸向進給運動的引入破壞了工件與車齒刀原本的傳動關系,因此在加工具有螺旋角的齒輪時,工件或車齒刀還需要額外增加一個回轉運動以形成齒輪齒槽螺旋線,這個運動被稱為差動運動,用 Δω 表示。若通過在工件上增加差動運動,此時工件完整的回轉運動如下所示:
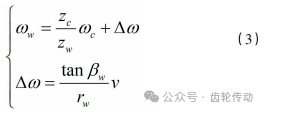
與機床結構一致,共設置 5 個坐標系與各運動部組相對應:Oh-xhyhzh 為車齒刀安裝坐標系,是和車齒刀初始位置重合的固定坐標系;O2-x2y2z2 為工件參考坐標系,是和工件初始位置重合的固定坐標系;O1-x1y1z1 為車齒刀參考坐標系,與工件參考坐標系相互平行;Oc-xcyczc 為車齒刀固連的運動坐標系;Ow-xwywzw 為與工件固連的運動坐標系。
根據齊次坐標變換原理,車齒刀坐標系和工件坐標系之間可以通過變換矩陣進行轉換。設車齒刀切削刃曲線已知,表示在車齒刀坐標中為 M=[x(u),y(u),z(u),1] T,通過齊次坐標變換,可以得到切削刃運動形成的空間軌跡曲面在工件坐標系 Ow-xwywzw 中齊次坐標方程為:
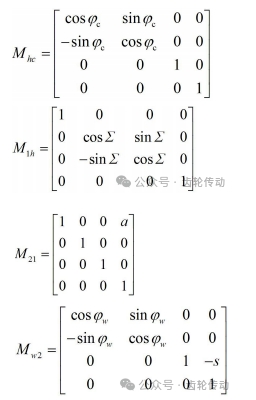
式中:Mhc、M1h、M21、Mw2 分別表示從車齒刀坐標系到車齒刀安裝坐標系、車齒刀安裝坐標系到車齒刀參考坐標系、車齒刀參考坐標系到工件參考坐標系、工件參考坐標系到工件坐標系的變換矩陣,其完整形式如下:
二、車齒成形齒面幾何數值仿真計算
車齒加工齒面成形過程分析
車齒加工實質是車齒刀與工件按照給定傳動比做同步回轉運動,由分布在車齒刀上的切削刃根據運動關系在空間中掠過生成一系列軌跡曲面,稱為掃掠面,掃掠面依次與工件相交并切除材料,最終形成了加工齒輪的表面形貌。
齒面包絡波紋誤差計算方法
理想漸開線圓柱齒輪的齒面可視為一條標準漸開線繞齒輪軸線做螺旋創成運動形成的空間漸開面。以漸開線展開角 θ 為參數,標準漸開線的參數方程表示為:

式中:rb 為工件齒輪基圓半徑。
設 M(Δ)表示漸開線生成漸開面的的齊次變換矩陣,以標準漸開線沿齒輪軸線的位移量 ζ 為參數,齒輪理論齒面的齊次坐標方程 F(θ,ζ)如式(6)所示:

式中:△包括漸開線做螺旋運動時與位移量ζ 對應轉過的角度和獲得齒槽寬的齒面張角。
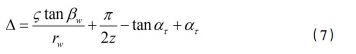
式中:ατ 為工件端面壓力角。
齒面包絡波紋誤差是沿理論齒面 F(θ,ζ)上一點的法向計算的,即齒面的法向誤差,理論齒面 F(θ,ζ)的法向量計算公式為:
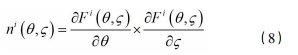
本文采用離散網格法計算齒面包絡波紋誤差,具體方法如下:將理想齒面 F(θ,ζ)的參數 θ 與 ζ 在其取值范圍內離散形成網格,網格區域面積設置為 m×l,步長設置為 Δθ 與 Δζ。用上標 m、l 對網格上離散點進行編號,F(θ,ζ) 在離散點(θm,ζl)的法向矢量表示為 ni(θ m,ζ l),其法向誤差表示為 hi(θm,ζ l)。
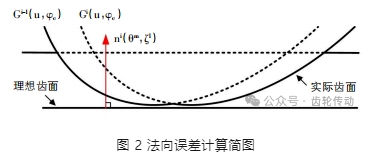
圖 2 為法向誤差計算示意圖,由圖中可知,理想齒面 F(θ,ζ)上離散點(θm,ζl)的法向矢量 ni(θm,ζl)會先后穿過不同的掃掠面,因此法向誤差值需分別計算 F(θ,ζ)的法向量與各個掃掠面之間的法向距離,取其中的最小值即為齒面的法向誤差值 hi(θm,ζl)。
三、齒面包絡波紋誤差影響因素分析
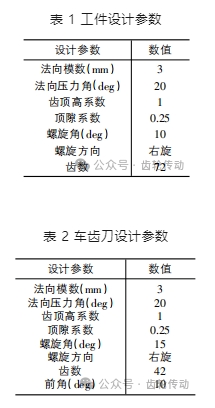
影響車齒加工質量的因素有很多,主要包括刀具幾何參數、切削參數、設備因素、環境因素等。本文對車齒加工過程中不同軸向進給量 f、刀具螺旋角 βc 和刀具前角 γ0 下成形齒面微觀形貌進行數值仿真計算,車齒刀和工件的設計參數如表 1 和表 2 所示。
各車齒工藝參數對齒面法向誤差的影響規律如圖 3、圖 4 所示。由圖可知,在試驗參數范圍內,保持刀具螺旋角或刀具前角不變的情況下,隨著軸向進給量的增大,齒面最大法向誤差值 Rmax 隨之增大,且變化幅值較大。這是由于軸向進給量的增加會導致刀具每齒切削厚度增大,波紋誤差的波距變大,刀齒在單位時間內切除材料的體積隨之上升,切削力隨之增大,故表面粗糙度增加,表面形貌變差。
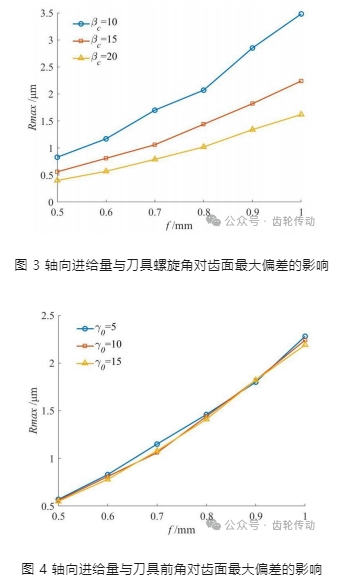
由圖 3 可知,隨著刀具螺旋角的增大,齒面最大法向誤差值 Rmax 隨之減小,且變化幅值較大。這是由于刀具螺旋角增大,軸交角隨之增大,增大軸交角可以提高刀刃切削性能,改善切削條件,從而降低表面粗糙度。但軸交角增大會減小接觸區域寬度,過大的軸交角反而會對加工精度產生不利影響,因此實際加工時需要綜合考慮多種因素以選擇合理的軸交角。
由圖 4 可知,隨著刀具前角的增大,齒面最大法向誤差值 Rmax 出現振蕩趨勢,但是振幅比較小且沒有明顯變化,可以認為刀具前角對理論加工誤差影響較小,基本可以忽略不計。
四、結論
本文為了研究車齒工藝中加工誤差的影響因素,通過分析車齒工藝原理,建立了車齒加工過程中切削刃空間軌跡曲面數學參數模型,然后采用離散網格方法計算了齒面包絡誤差,在此基礎上分析車齒工藝參數對齒面包絡波紋誤差的影響程度。本研究得到如下結論:①軸向進給量和刀具螺旋角對齒面包絡波紋誤差有較顯著的影響,刀具前角對包絡波紋誤差的影響較小;②通過增大刀具螺旋角或者減小軸向進給量可以提高車齒加工精度。
參考文獻略.
