為更準確表達柔輪變形后的輪齒的位置,課題組最先提出柔輪中性層變形曲線的精確算法,計算變形后柔輪齒圈切向位移引起的轉角和輪齒對稱線相對于徑矢的轉角、及其變形后嚙合端齒廓的共軛位置。從設計角度看,為了增大承載能力,提高傳動剛度,應考慮如何獲得更寬的包絡存在區(qū)間,使更多的齒參與嚙合。課題組對公切線型雙圓弧齒廓進行了設計研究(圖6a),經(jīng)過合理設計的雙圓弧齒廓能夠在齒頂和齒根實現(xiàn)二次共軛(圖6b),并因其具有優(yōu)良的共軛設計性能,其側隙分布結果(圖6c)相對漸開線齒廓也更小、更平均。
(2) 三圓弧齒廓
公切線型雙圓弧齒廓雖然具有較大的共軛區(qū)間,但其公切線特征使得其共軛區(qū)間并不連續(xù)。為此,課題組提出了將公切線重新設計為公切圓弧的新型三圓弧齒廓設計方案(圖6d、e),三圓弧齒廓通過中間圓弧的設計,實現(xiàn)了齒頂和齒根連續(xù)的共軛嚙合區(qū)間(圖6f),共軛嚙合區(qū)間相比公切線雙圓弧齒廓顯著增大。三圓弧齒廓的包絡存在區(qū)間顯著增大,參與共軛嚙合的齒對數(shù)增多,可有效提高承載能力。
(3) 擺線齒廓
諧波齒輪柔輪變形后與剛輪間的相對運動軌跡近似呈擺線特征,課題組從嚙合運動軌跡的曲線特征出發(fā)提出了一種變系數(shù)擺線齒廓(圖6g)及其設計方法。變系數(shù)擺線齒廓主要由齒頂擺線和齒根擺線構成,兩段齒廓之間可以由公切線連接。與雙圓弧齒廓類似,變系數(shù)擺線齒廓的齒頂和齒根也具有多次共軛的現(xiàn)象,其具有從短軸到長軸的連續(xù)共軛范圍(圖6h)。由于系數(shù)的可設計性,變系數(shù)擺線齒廓可以獲得更加均勻的微小側隙(圖6i)。
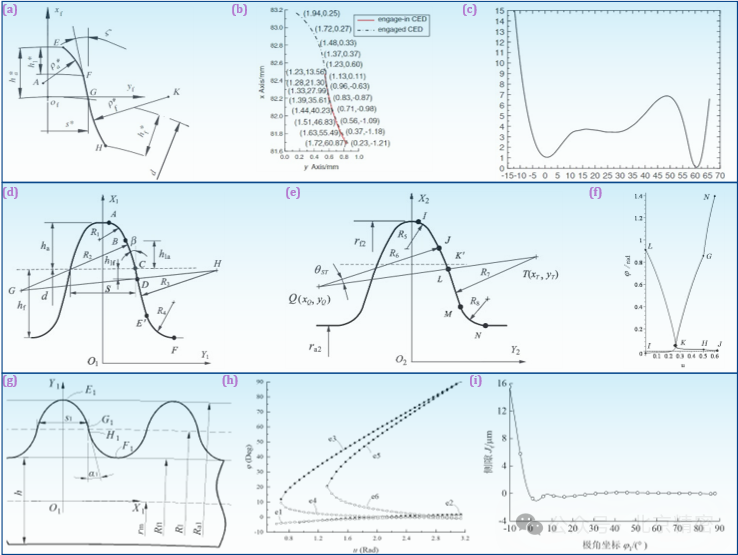
圖6 雙圓弧、三圓弧及擺線齒廓設計:(a) 公切線型雙圓弧齒廓; (b) 雙圓弧齒廓的二次共軛設計; (c) 雙圓弧齒廓的嚙合側隙; (d) 三圓弧柔輪齒廓; (e) 三圓弧剛輪齒廓; (f) 三圓弧齒廓的共軛范圍; (g) 變系數(shù)擺線齒廓; (h) 變系數(shù)擺線齒廓的共軛范圍及多次共軛; (i) 變系數(shù)擺線齒廓的嚙合側隙.
2.2 三維齒形共軛設計與修形(1) 線接觸連續(xù)共軛三維齒形通過在沿齒圈軸向分布的多個截面上進行共軛計算,可以近似獲得諧波齒輪的共軛三維齒形,這種齒形在每個截面上都可以獲得各自的大共軛范圍嚙合。課題組以變系數(shù)擺線齒廓為例,進行了線接觸連續(xù)共軛三維齒形的設計(圖7a)。這種齒廓不僅可以在從短軸到長軸的整個嚙入?yún)^(qū)進行共軛嚙合,在長軸往短軸去的小部分區(qū)域內(nèi)也具有共軛嚙合特性,將共軛區(qū)間擴展至超過90°。線接觸連續(xù)共軛三維齒形具有在較大范圍內(nèi)優(yōu)異的共軛能力,但由于齒廓沿齒向持續(xù)變化,因此加工困難。(2) 點接觸連續(xù)共軛三維齒形如果以單一截面的共軛齒廓做圓柱直齒輪方案,則會在齒圈設計截面前后出現(xiàn)不同的干涉(圖7b)。為了避免干涉并獲得易于加工的連續(xù)共軛齒形,課題組提出了多截面共軛再包絡的齒形及其設計方法:以公切線型雙圓弧齒廓為例,對多個截面上柔輪齒廓進行共軛計算,并對共軛結果進行再包絡,獲得最終的剛輪齒廓(圖7c)。該方案的三維齒形中,柔輪和剛輪在短軸到長軸的嚙合運動中,共軛嚙合點從齒頂?shù)烬X根、從后端往前端持續(xù)移動實現(xiàn)了連續(xù)的共軛嚙合。該方案齒形在每個截面上都顯著減小了共軛區(qū)間,會導致嚙合性能的損失。
(3) 近似共軛的徑向變?yōu)樾扌稳S齒形對柔輪齒形沿軸向做連續(xù)徑向變?yōu)樾扌我部梢杂行П苊鈬Ш细缮妗Un題組以三圓弧齒廓為例進行了多截面連續(xù)徑向變?yōu)樾扌锡X形的設計研究(圖7d),在修形前,除齒廓設計截面外,其余截面上都出現(xiàn)了不同程度的嚙合干涉(圖7e),修形后消除了嚙合干涉現(xiàn)象(圖7f)。同時,在徑向變?yōu)樾扌魏螅鱾€截面上柔輪與剛輪的嚙合齒對都處于近似共軛的嚙合狀態(tài)(圖7g)。徑向變位修形的齒形方案加工工藝成熟方便,是工程中應用最廣泛的方案。
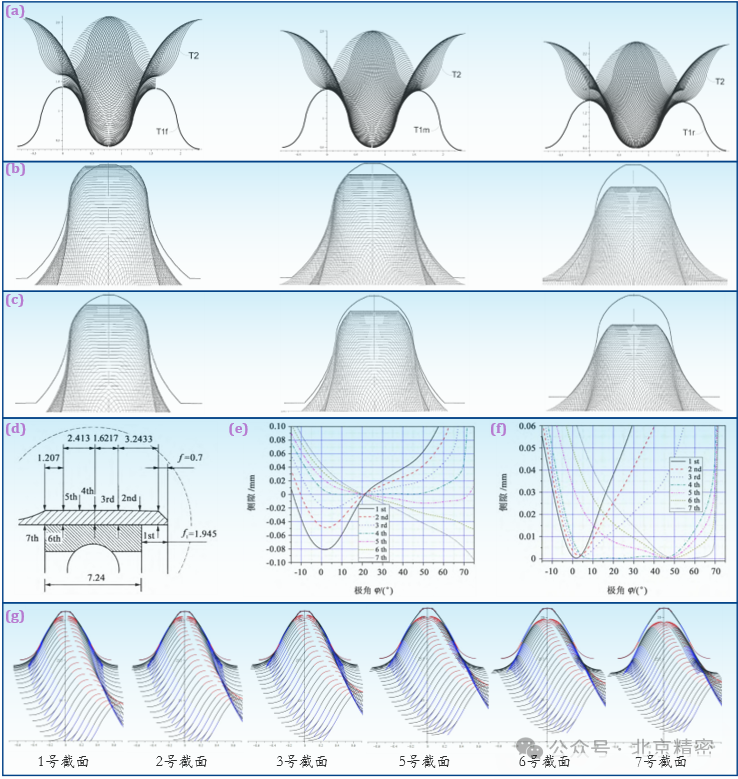
圖7 三維齒形共軛設計與修形:(a) 線接觸連續(xù)共軛三維齒形設計; (b)-(c) 點接觸連續(xù)共軛三維齒形設計; (d-g) 近似共軛的徑向變?yōu)樾扌稳S齒形.
2.3 柔輪的滾齒誤差分析當前,由于工藝和技術理論相對成熟和成本低廉等有點,漸開線齒廓依然在諧波齒輪中擁有一定的應用比例。但是標準滾刀加工大變位漸開線齒廓極易產(chǎn)生大的加工誤差,影響最終的嚙合質量和傳動性能。課題組基于滾齒仿真計算研究大變位齒輪成形機理,分析柔輪齒面理論加工誤差值及產(chǎn)生原因。建立了滾刀系列切削刃參數(shù)化方程,并結合滾齒參數(shù)及滾齒時滾刀和工件相互運動關系建立變位齒輪滾切成形數(shù)學模型,基于滾齒多刃切削成形特征建立齒面理論加工誤差評價模型進行滾齒加工誤差仿真計算。
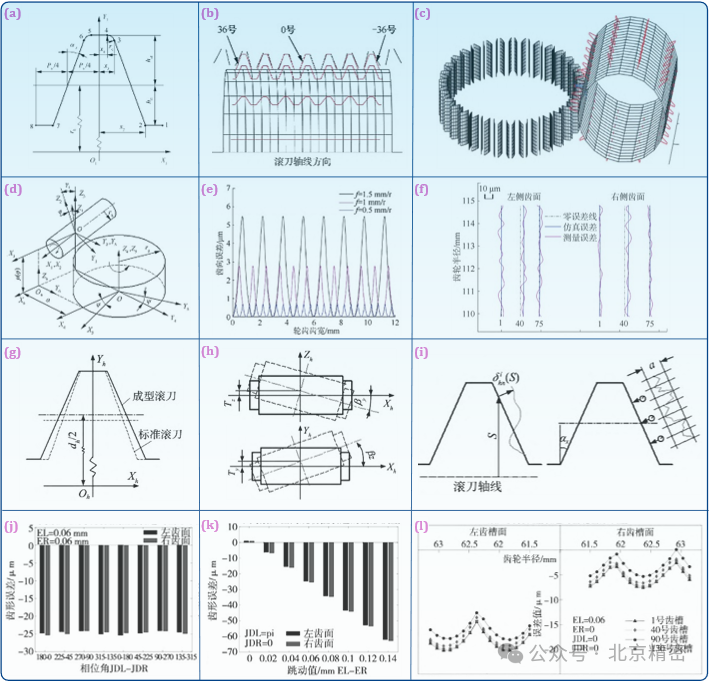
圖8 滾齒加工誤差分析:(a) 滾刀軸向齒形; (b) 滾齒仿真截面示意圖; (c) 加工仿真; (d) 滾刀空間運動關系; (e) 不同軸向進給量下的齒向誤差; (f) 左右側齒面的齒向誤差; (g) 成型滾刀軸向齒形; (h) 滾刀安裝誤差示意圖; (i) 滾刀切削刃齒形誤差示意圖; (j) 滾刀跳動相位角對齒形誤差的影響; (k) 滾刀跳動值對齒形誤差的影響; (l) 滾刀安裝誤差引起的齒形誤差.
(待續(xù))
