螺旋錐齒輪是核心傳動元件,廣泛應用于車輛、飛機和船舶等裝備。在傳遞動力的過程中,傳動系統受載變形會導致齒輪副的嚙合狀態產生偏移,影響齒輪副的傳動性能。通常要結合齒輪副的嚙合錯位結果開展齒面設計與修形。因此快速準確分析傳動系統的嚙合錯位情況,對評估齒輪副的加載嚙合性能和優化齒面設計非常重要。
國內外學者對齒輪傳動系統的嚙合錯位量分析方法進行了大量的研究。王欽等建立了多支撐軸系耦合分析模型,綜合考慮軸承剛度、齒輪、軸和殼體的影響求解齒輪嚙合錯位量,并通過實驗進行驗證。高潔等綜合考慮了機匣、軸系及軸承的支撐變形對齒輪軸線偏移的影響對當量錯位量疊加,在此基礎上對弧齒錐齒輪齒面修形。覃秋霞等考慮了機匣的加工誤差、軸承的過盈配合等因素建立嚙合錯位量計算模型,基于計算結果對弧齒錐齒輪齒面進行設計,用實驗驗證嚙合錯位后的印痕和傳動誤差。賴長發等借助 Masta 軟件建立了驅動主減速器的仿真分析模型計算螺旋錐齒輪的嚙合錯位量,將仿真分析結果與實驗作對比。然而為了快速獲得計算結果,上述研究在分析傳動軸的變形時,大多將傳動軸簡化為梁單元模型。但這種簡化處理忽略了歐拉梁、鐵木辛柯梁理論推導的假設條件,當傳動軸結構復雜時,其變形分析結果可能會產生較大的誤差,導致齒輪傳動系統的嚙合錯位量計算不準確,從而影響齒面優化設計效果。
針對以上問題,本文提出一種基于實體有限元法的分步螺旋錐齒輪傳動系統嚙合錯位分析方法。該方法考慮軸承剛度和齒輪嚙合力的影響,采用實體有限元模型進行傳動軸的變形分析保證齒輪副嚙合錯位量計算的準確性,以此為基礎建立包含嚙合錯位影響的輪齒加載接觸分析以大幅度提高計算分析效率。
一、齒輪副嚙合錯位量計算
嚙合錯位量的定義
齒輪傳動系統包括軸、軸承和齒輪等零件,且結構復雜。傳動系統工作時,齒輪副的嚙合力傳遞到軸和軸承上,導致系統產生變形,從而使齒輪的相對安裝位置發生偏移。齒輪副在載荷作用下安裝位置的偏移量即為齒輪副的嚙合錯位量,如圖 1 所示。
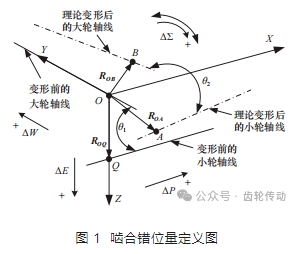
軸交錯點變形前為 O、Q,變形后為A、B 。齒輪軸線變形前用細實線表示,理論變形后用點劃線表示,ROA、ROB、ROQ 是點O 到 A、B、Q的向量。軸交錯點的偏移矢量為
將其分解到初始齒輪坐標系中,則嚙合錯位量的計算公式為
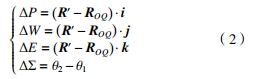
式中:?P為齒輪副沿小輪軸向的相對位移量;?W 為沿大輪軸向的相對位移量;?E為沿偏置方向的相對位移量;?Σ為沿軸交角方向的相對變化量;i、j、k為初始坐標系中坐標軸的單位矢量;θ1、θ2 為變形前后的軸交角。
嚙合錯位量的計算方法
圖 2 所示為齒輪副嚙合錯位量的計算原理圖。初始坐標系Σq = {O; x, y,z} x、y、z為X、Y、Z軸的矢量;彎矩坐標系Σqy = {O; x ′, y ′,z ′} x ′、y ′、z為X ′、 Y ′、Z ′軸的矢量。
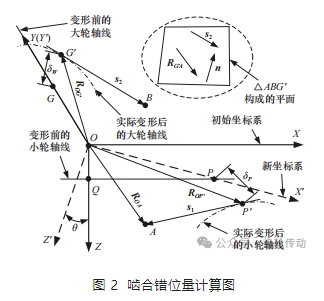
P、G 是變形前小、大齒輪齒寬中點在齒輪軸線上的投影點。受載變形后點 P、G 變成了點P ′、G ′ ,δP、δW分別是點 P到P ′ 以及G 到 G ′ 的距離。實際變形后軸線變成曲線用點劃線表示,在點P ′、G ′處分別作兩條曲線的切線,其方向向量為s1 和 s2。則兩個 方向向量的法矢 n 為
設s3 是點 P ′ 和 G ′連線的矢量,設向量 s1和 s2之間的距離為lE 和角度為θS ,計算公式為
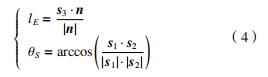
設小輪等效軸線上點A 與 P ′之間的距離為lP2,則建立包含 lP2 的方程表達式為
式中:ROP′為點O 和 P ′連線的矢量。
構建包含向量 s2 和法向量 n 的平面,其中點 A、B、G ′ 在該平面內,則RG′A 滿足
式中:ROG′ 為點O 和G′ 連線的矢量;RG′A 為點G ′ 和 A 連線的矢量。
設大輪等效軸線上點B 與 G ′ 之間的距離為 lW2,計算公式為
將系統變形前后的參數疊加,獲得齒輪副的嚙合錯位量。
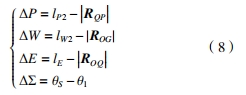
式中:RQP 為點 Q和 P連線的矢量;ROG為點O 和 G 連線的矢量。
二、不同計算模型的傳動軸變形分析對比
傳動軸的受載變形是導致齒輪副嚙合錯位的主要影響因素,因此準確計算傳動軸的變形量至關重要。傳動軸大多簡化為梁單元模型,其變形分析原理如圖 3 所示。
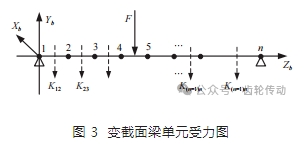
根據傳動軸的截面情況將其分段,用兩個節點和一個梁單元表示相同截面的軸段。整根傳動軸則可表示為由若干個不同截面的梁單元組合,其節點個數比單元個數多 1。每個節點包含 6 個自由度, 因此每個相同截面的梁單元可以用一個 12×12 的剛度矩陣表示。
將整根傳動軸中每一段兩節點的梁單元剛度矩陣進行疊加,得到整根傳動軸的總剛度矩陣如下:

式中:K(n−1)n為 2×2 的剛度矩陣;矩陣 K(n−1)n包含![]() 是節點 (n−1)和 n所在梁單元中在節點 n−1處的剛度;
是節點 (n−1)和 n所在梁單元中在節點 n−1處的剛度;![]() 為節點n處的剛度;A(n−1)n、An(n−1)為耦合剛度,且每個剛度都是 6×6 的矩陣,其余剛度以此類推。
為節點n處的剛度;A(n−1)n、An(n−1)為耦合剛度,且每個剛度都是 6×6 的矩陣,其余剛度以此類推。
根據力與變形之間的關系,構建梁的力平衡方程如下:
式中:Fn 為節點n處的載荷子矩陣;δn為變形子矩陣,兩者都為 6×6 的矩陣。
已知外力和總剛度矩陣,通過平衡方程計算出梁單元在各節點上的變形量。
以某個復雜傳動軸為例,首先根據傳動軸的軸段數量來確定梁單元的初始節點數目,然后以載荷施加位置、邊界條件及軸的變形提取位置進一步增加節點數量,最后通過這些節點去建立完整的梁單元模型如圖 4 所示。節點 2 和節點 16 是支撐位置。節點 5~節點 9 是位移變形量的提取位置,節點 7 為載荷施加位置,其余節點是軸段的分界位置。
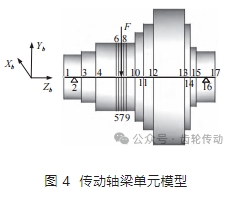
軸的材料為 20CrMnTi,泊松比為 0.3。在節點 7 處施加 3 個方向上的集中力,分別為 1 700、1 200、2 000 N。在節點 2 和節點 16 處添加邊界條件,需要約束除了軸線回轉方向之外的其余 5 個自由度。
為了對比不同模型分析軸變形的誤差情況。同時按照圖 4 的結構去構建軸的實體有限元模型,其材料、受力情況以及邊界條件與梁單元模型的設置相同。通過靜力學分析得到兩種計算模型傳動軸的變形如圖 5 所示。

為了直觀地對比兩種模型的傳動軸變形情況,提取軸線上節點的變形量,見表 1。
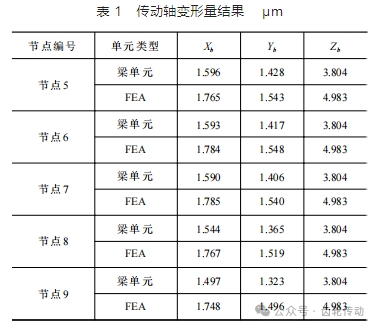
由表 1 可知,采用梁單元模型計算的傳動軸變形量在各方向上與實體有限元模型相比均存在一定誤差,徑向方向(Xb、Yb)誤差約 13%~16%,沿軸線方向(Zb)誤差更大,約 30%。因此傳動軸結構復雜時,不能用梁單元模型代替實體有限元模型去分析其受載變形情況。這種誤差可能來源于梁單元模型受載變形后的梁截面與軸線關系的假設。
三、分步式嚙合錯位分析模型
綜上所述,采用梁單元模型計算傳動軸受載變形會在各方向上產生較大誤差。為了提高變形分析的準確度,有學者研究通過實體有限元構建包含傳動軸、齒輪以及軸承的傳動系統全有限元模型,通過接觸對定義齒面的嚙合關系進行系統嚙合錯位的分析。這種方法能較好地提高計算精度,但是網格數量多,劃分困難,非常耗費計算資源。為了保證計算分析的準確性,同時提高計算效率,本文提出一種基于實體有限元法的分步螺旋錐齒輪傳動系統嚙合錯位分析方法:僅將傳動軸構建為實體有限元模型,軸承等效為剛度矩陣耦合于傳動軸上;將齒輪副傳遞的載荷等效為嚙合力;采用靜力學有限元法分析傳動軸變形,進而計算齒輪副的嚙合錯位量;根據嚙合錯位量構建輪齒的加載接觸分析模型分析齒面的接觸偏移情況。
傳動軸耦合分析模型
首先建立包含軸承影響的傳動軸變形耦合分析模型,如圖 6 所示。依據傳動軸不同軸段去劃分網格,為了減少網格數量,全部劃分為六面體單元。再根據軸承安裝位置、嚙合力施加位置以及變形量提取位置對網格進行調整。
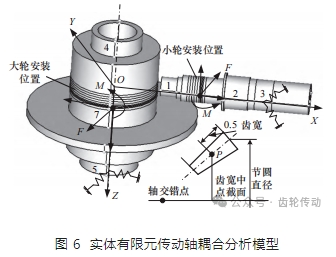
圖 6 中軸段 1~5 為軸承安裝位置,將這些軸段上軸承等效受力點處建立導向點,并將軸承與對應軸段上表面網格進行耦合。考慮軸承的彈性特征可以用彈簧來等效。每個導向點會通過 5 個彈簧約束其除回轉方向之外的 5 個運動自由度,每個導向點在各方向彈簧的剛度由軸承的剛度矩陣中主對角元的數值確定。
軸段 6 和軸段 7 為大、小齒輪安裝位置,在該軸段需要施加齒輪嚙合力,同時需要提取傳動軸受載變形量。通常將齒寬中部的節點位置定義為接觸區的中心位置。若將嚙合力施加在傳動軸上時,會在齒寬中點 P 處切割出一個軸截面(P 點的位置如圖 6 所示),在軸心位置建立導向點并與截面耦合,并在該導向點上添加嚙合力和彎矩。另外將該軸段等分切割成若干個子軸段,按照從左到右的順序依次在軸心位置建立若干個導向點并與對應的軸截面耦合。通過以上處理,齒輪在安裝位置的變形可由各導向點的位移表示。
等效嚙合力計算
為了減少齒面接觸分析的計算量,將齒輪接觸作用等效為嚙合力。根據傳動扭矩計算節點處的切向力Fmt,考慮螺旋錐齒輪參數進一步計算出軸向力 Fax和徑向力 Frd。以上計算的嚙合力是作用在齒面上的,而 3.1 節所述的計算模型其嚙合力作用于軸線上。力的作用點改變后需要采用力的平移定理重新計算載荷。其中徑向力朝著軸心位置平移不產生彎矩,切向力產生繞軸線回轉方向的彎矩不影響變形,軸向力產生其余方向彎矩會影響變形。
小輪坐標系 ΣP={Q; xP, yP, zP}與初始坐標系 Σq 在 z 方向的距離為偏置距,xP 是小輪回轉軸,小輪軸向力產生 zP 方向的彎矩:
當齒輪副的偏置距為 0 時,大輪的彎矩計算方式與小輪相同。但偏置距不為 0 時,大輪軸向力產 生彎矩的方向與 z 方向有一定的角度,則在大輪軸心導向點處的彎矩坐標系Σqy 與嚙合力坐標系Σq 不同。為了避免在同一個導向點施加嚙合力和彎矩需要添加兩個不同的坐標系問題,以彎矩坐標系Σqy 為主,將切向力和徑向力分解到坐標系Σqy 中,計算公式為
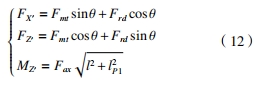
式中:FX′、FZ' 為坐標系Σqy 中 x ′與 z'方向的力;MZ ′ 為 z'方向的彎矩。
在小輪坐標系 ΣP中齒寬中點所在軸截面的導向點處施加嚙合力與彎矩;在大輪坐標系 Σqy 中齒寬中點所在軸截面的導向點處施加嚙合力與彎矩。
考慮嚙合錯位的輪齒加載接觸分析
將 3.2 節計算的等效嚙合力代入 3.1 節所述的傳動軸變形耦合分析模型,導出該模型中傳動軸軸線上多個導向點的位移變形量,將其代入 1.2 節的公式求出系統的嚙合錯位量。通過嚙合錯位量去調整多齒嚙合模型中齒輪的位置及姿態。首先將大輪沿著全局坐標系的Y 軸移動?W,然后以大輪為基準將小輪分別沿著局部坐標系的 X1、Z1軸分別移動 ?P、?E,最后將小輪繞軸 Y1旋轉 ?Σ,從而構建出包含嚙合錯位的輪齒加載接觸分析模型,如圖 7 所示。
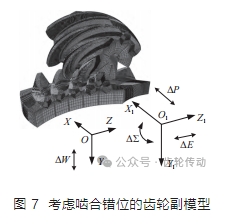
輪齒齒面通過接觸對建立嚙合作用。在大小齒輪寬中部的軸線中心建立載荷作用參考點,分別與齒輪的輪轂面建立耦合作用以便施加載荷。大輪參考點施加工作扭矩,小輪參考點施加轉角,同時約束除齒輪回轉自由度外的其余自由度。采用靜力分析方法進行計算,則可獲得某嚙合瞬時齒面的接觸狀態以及齒輪的實際轉角。改變小輪轉角進行多步計算,則可得整個嚙合過程中齒輪副的加載傳動誤差及接觸印痕。
四、計算實例
嚙合錯位量計算對比
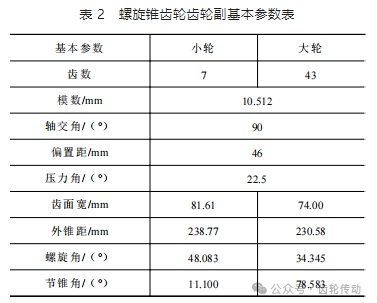
為了檢驗本文提出的實體有限元法分步螺旋錐齒輪傳動系統嚙合錯位分析方法的準確性,以某客車驅動橋為例進行齒輪副嚙合錯位分析。其中螺旋錐齒輪基本參數見表 2。
齒輪副的額定工作扭矩為 15 000 N·m,利用 3.2 節所述的計算公式得到嚙合力和彎矩計算結果,見表 3。
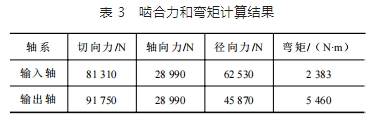
參考多支撐軸系中軸承單元剛度計算公式[11] 計算傳動系統中軸承剛度矩陣,導出各軸承剛度矩陣中在主對角元上的數值,見表 4。
采用上述參數與傳動軸圖紙可以建立傳動軸耦合分析有限元模型,計算獲得傳動軸的變形量及齒輪副的嚙合錯位量。同時建立圖 8 所示的傳動系統全有限元模型與本文方法做對比分析。由于齒輪與傳動軸結合部位六面體網格劃分困難,因此輪齒部分采用四面體進行網格劃分。該模型中的材料屬性、傳動軸的設置方式與 3.1 節所述模型相同。齒面嚙合作用參考 3.3 節接觸對設置。添加邊界條件時,需注意在施加工作扭矩和轉角的參考點處約束自由度,除了軸線回轉自由度外,其余自由度將由軸承的等效彈簧約束。
同時以梁單元構建傳動系統模型進行系統的嚙合錯位分析,分別提取三種模型傳動軸軸線上節點處的變形量。其中全有限元模型齒輪嚙合位置是時刻變化的,因此提取五齒模型中第三齒在節點嚙合時的變形量。最終繪制出傳動軸的變形結果,如圖 9 所示。
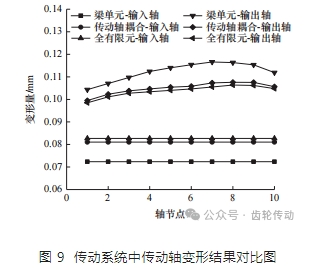
對比分析梁單元模型與全有限元模型的傳動軸變形結果,其平均誤差輸入軸約為 12.4%、輸出軸約為 10.2%。比較實體有限元傳動軸耦合分析模型與全有限元模型的傳動軸變形結果,其平均誤差輸入軸約為 1.9%、輸出軸約為 1.2%。考慮到梁單元計算結果誤差較大,將傳動軸的變形量代入 1.2 節 的計算公式得到錯位量,見表 5。
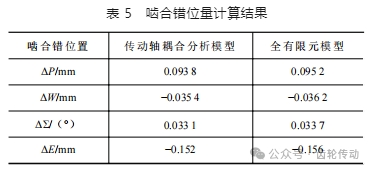
由表 5 可知,傳動軸耦合分析模型與全有限元模型的嚙合錯位量誤差在 2.5% 以內。
加載印痕和傳動誤差對比
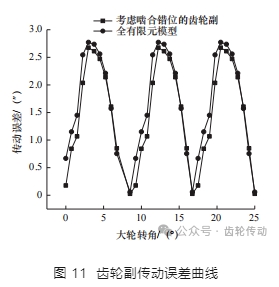
將每一嚙合瞬時的齒面接觸位置的應力提出疊加到齒面上可獲得齒面的加載接觸印痕,本文所述方法計算的加載印痕如圖 10a 所示,全有限元模型計算的加載印痕如圖 10b 所示,兩者的傳動誤差結果如圖 11 所示。

由圖 11 可知,分步螺旋錐齒輪傳動系統嚙合錯位分析方法得到的加載印痕與全有限元模型計算的加載印痕位置及形狀均一致,僅在齒寬方向有細微差異,其加載傳動誤差曲線形態吻合,幅值偏差在 1.3% 左右。
分步螺旋錐齒輪傳動系統嚙合錯位分析方法分為兩部分:傳動軸耦合變形分析模型部分的網格數約為 18.5 萬;考慮嚙合錯位的輪齒加載接觸分析模型網格數約為 80.4 萬(齒面接觸部分網格大小為 0.2 mm)。全有限元模型網格數量約為 308 萬(齒面接觸部分網格大小為 0.4 mm)。統計兩種分析模型的計算時間,見表 6。

由表 6 可知,分步螺旋錐齒輪傳動系統嚙合錯位分析方法的分析時間相比全有限元模型大幅減少。若將全有限元模型的齒面網格劃分為 0.2 mm,則分析時間還將進一步增加。
五、結語
針對傳動軸結構復雜時采用梁單元模型求解軸的變形差異較大,會導致齒輪副嚙合錯位分析不準確的問題,本文提出一種基于實體有限元法的分步螺旋錐齒輪傳動系統嚙合錯位分析方法。通過理論研究以及仿真分析得出以下結論:
(1)傳動軸模型結構復雜時,采用梁單元模型求解軸的受載變形與實體有限元模型計算結果存在較大誤差。
(2)提出的基于實體有限元模型的傳動軸變形耦合分析模型,綜合考慮了齒輪嚙合力作用以及傳動軸結構柔性與軸承支撐柔性耦合狀況,能夠更為準確地分析螺旋錐齒輪傳動系統傳動軸的受載變形情況。
(3)提出的基于實體有限元法的分步螺旋錐齒輪傳動系統嚙合錯位分析方法能夠準確分析齒輪副的加載印痕及傳動誤差,在保證計算精度的同時,計算效率明顯提升。
參考文獻略.
