齒輪作為當代社會各種機械設備中重要的組成元件之一,已經遍布在汽車、航天、電器以及精密測量儀器等領域。隨著當前自動化、信息化以及智能化成為未來的發展趨勢,對機械設備的精度要求也越來越高,作為其中之一的齒輪也是目前的研究熱點。當前對齒輪的加工工藝已經非常成熟,而如何實現快速、自動的測量對提高齒輪的加工效率具有重大的意義。
齒輪的測量精度高低,不僅與選取的測量方法有關,還與測量設備本身的精度有關,選取的測量設備越合適,測量設備的精度等級越高,將會使齒輪的測量精度越高,進而提高齒輪的制造精度。齒輪測量技術發展近百年,從最開始的量具測量到“Tooth Surface Tester”,接著出現機械展成式測量,再到坐標法測量。在 20 世紀 80 年代,日本推出非接觸齒面分析機 FS—35,標志著非接觸式測量的開始。在齒輪的測量技術上,歷經了“以機械為主”到“機電結合”,直至當今的“光機電”與“信息技術”綜合集成的演變。
國內外諸多學者對齒輪測量展開了研究,解鵬輝在 CNC 齒輪測量中心中展開了對弧齒錐齒輪齒面偏差測量,實現了對弧齒錐齒輪的齒距偏差和齒面偏差的測量。武冠宏等人在三坐標測量機下,對螺旋錐齒輪進行了測量,得到了螺旋錐齒輪的齒面偏差和齒距累積偏差; 同時對測量數據進行了分析處理,將其與普通齒輪檢測儀的測量數據進行對比,發現其誤差明顯小于普通齒輪檢測儀的測量數據,測量精度高,可為齒面修型及機床參數調整等數據提供指導。張衛青等人展開了基于三維掃描式測頭的弧齒錐齒輪的測量,并對誤差進行了分析處理,經過實驗,驗證了其可行性,提高了測量數據準確性以及測量效率。熊文豪等人利用數字圖像處理技術對齒輪尺寸進行了測量,由實驗證明,該方法可以快速地進行齒輪參數尺寸的檢測,且精度較高。程敏杰等人結合了機器視覺技術,對直齒輪展開了非接觸式測量,得到了齒輪的基本尺寸參數以及齒距偏差,并對其進行了相應的誤差分析; 通過實驗,將理論值與實際值進行了對比,證明了采取機器視覺技術進行齒輪測量的可行性,為直齒輪在機測量提供了一種新思路。
然而,針對超精密齒輪測量展開工作還是很少,且大多數都是使用三坐標測量機對齒輪進行檢測,暫時還沒有學者和研究人員使用線結構光對齒輪進行相關的測量。本文采用線結構光測量系統對齒輪進行測量,以期能夠提高齒輪測量精度與效率,并為在機測量生產提供新的思路。
一、線結構光測量原理及系統
線結構光測量原理及系統組成
當前對于齒輪的測量方式主要分為非接觸式測量和接觸式測量。接觸式測量作為一種已經發展了近百年的測量技術,已經發展的很成熟。三坐標測量機就是接觸式測量中最典型的設備,但是其也有局限性和缺點,在測量時因為與被測物體直接接觸,容易在被測物體表面造成劃傷、劃痕等; 同時還有測量力的存在,造成測量表面的輕微變形,影響了測量精度; 并且測量精度范圍有所局限,當面臨超高精度或大批量的產品測量時,使用接觸式測量就不太經濟 實用。非接觸式測量技術以光、電、機以及計算機等技術為基礎,在測量儀器不與被測物體發生接觸的條件下,通過測量與收集以及計算機的分析即可得到所需的被測物體的參數信息。當前主流的非接觸式測量方法主要分為兩種: 光學法與非光學法。光學法使用最為廣泛,其可細分為激光三角法、激光測距法、圖像分析法、結構光法以及干涉測量法。
結構光法的基本原理是激光器發射出結構光,投射于被測物體表面,光條紋經物體表面后發生形變,其形變大小主要由物體的表面形狀( 即物體的加工精度) 決定,形變后的光條紋經相機收集,再通過計算機系統進行進一步的分析、量化與處理后,在計算機上展現被測物體的三維圖像與具體參數,進而使用這些參數去求解需要的數據。
結構光三維測量系統由結構光投射器(激光器) 、工業相機(CCD 相機) 、移動實驗臺及計算機等組成,其理論依據是激光三角測量原理,如圖 1 所示。
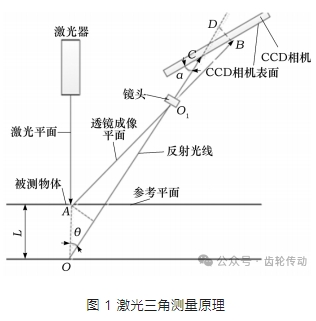
圖 1 中: 點 A 為被測物體在參考平面的基準點; 點 L 為被測物體偏離參考平面基準點的距離; 點 O 為點 A 偏離參考平面基準點所在的點; 點 O1 為反射光線與透鏡成像平面在鏡頭處的交點; 點 B 為透鏡成像平面與 CCD 相機表面的交點; 點 C 為反射光線與 CCD 相機表面的交點; 點 D 為點 O1 經反射后在 CCD相機處的聚焦點; α 為反射光線與 CCD 相機表面之間的夾角; θ 為激光平面與反射光線之間的夾角。
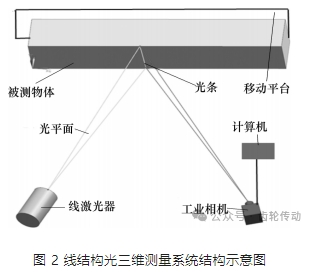
線結構光測量系統就是結構光測量系統中的激光器是線激光器,發射出的光是線結構光。線結構光三維測量系統(簡稱線結構光測量系統) 主要由一臺計算機、工業相機、工業鏡頭、線激光器和移動平臺組成,線結構光三維測量系統結構示意圖如圖 2 所示。
線結構光測量系統測量誤差分析
線結構光測量系統的綜合誤差主要來源于 3 個方面,分別為 CCD 相機標定、線結構光視覺模型標定以及光條中心點檢測。在線結構光測量系統中,先對 CCD 相機進行標定,再進行線結構光視覺模型標定,最后對線結構光光條中心點進行檢測,其精度主要取決于檢測算法。不管如何進行標定或選擇算法,誤差總是無法避免的,且由于每次的誤差無法完全補償,誤差將會在后續的過程中得到疊加,最后呈現出一個整體的綜合誤差。
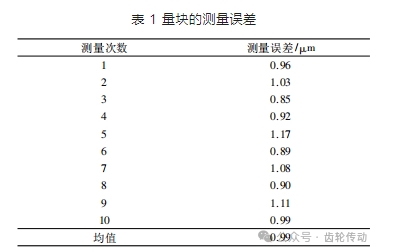
在完成上述 3 個誤差的標定及檢測后,對其展開測量誤差的評定,選取長度為 4 mm 的三等量塊進行重復性試驗,最終取其均值作為線結構光的測量系統綜合誤差。量塊的測量誤差見表 1。
采用線結構光測量系統進行齒輪的測量時,除了線結構光測量系統本身的誤差外,還會存在齒輪安裝誤差、頂尖同軸度誤差、測量重復性誤差等,但是這些誤差遠遠小于線結構光測量系統本身的誤差,因此,線結構光測量系統的精度是影響整個系統精度的主要因素。
二、齒距偏差
齒輪的齒距偏差指的是生產制造出來的齒輪齒距與理論上的齒輪齒距之間出現的偏差,它表示各齒的齒寬在圓周上分布的均勻程度。由于理論上的齒距是一個定值,然而實際制造中總是存在著設備、環境以及人工等影響因素,它們都影響著實際齒距的數值,因此,齒距偏差也是齒輪制造好壞以及齒輪制造精度的一個評判標準。因實際齒距與理論齒距之間存在偏差,齒輪在嚙合傳動時也受到其影響,在實際嚙合時會造成嚙合沖擊、振動等,故齒距偏差主要影響了齒輪傳動的平穩性、使用壽命以及傳動時的噪聲值等,因此,對齒距偏差進行分析與測量有著重要的意義。根據 ISO 1328—1: 2013《圓柱齒輪精度標準》的論述可知,該標準對齒距偏差各項指標的定義、評定方法以及評判標準作出了最新的說明; 其中,齒距偏差的評定指標分為了 4 部分,分別為任一單個齒距偏差 fpi、單個齒距偏差 fp、任一齒距累積偏差 Fpi 以及齒距累積總偏差 Fp。
單個齒距偏差 fp 和齒距累積總偏差 Fp 分別屬于影響齒輪工作平穩性、機械振動和噪聲以及傳遞運動準確性的重要誤差因素,并成為齒輪精度標準中重要的誤差分項。與此同時,國際標準中規定的齒輪測量的 4 個必檢項目中,單個齒距偏差 fp 和齒距累積總偏差 Fp 是其中之二。
任一單個齒距偏差 fpi 是指沿齒輪測量圓的橫截面中的實際齒距與相應的理論齒距的代數差,該值也為任一齒面的理論齒面與相鄰齒的同側齒面之間的位移值大小。對于同一齒輪 fpi的數值個數,無論是左齒面還是右齒面,它的個數只與齒輪的齒數相關,兩者在數值上相等。
在 ISO 1328—1: 2013 中,對任一單個齒距偏差 fpi 的數值正、負做出規定: 在規定的測量方向上(逆時針或順時針) ,當某一齒的實際齒距值比理論齒距值大時,兩者之差為該齒的任一單個齒距正偏差; 同理,當某一齒的實際齒距值比理論齒距值小時,兩者之差為該齒的任一單個齒距負偏差; 上述結果均保留其正、負值符號,求出值為正,即為正(+) 偏差,求出值為負,即為負(-) 偏差。對左、右齒面的 fpi測量應分別進行。
單個齒距偏差 fp 指的是被測齒輪全部任一單個齒距偏差 fpi 中絕對值最大的數值,無正、負之分。只要求出被測齒輪的全部任意單一齒距偏差,通過其定義即可求出對應的單個齒距偏差。同一齒輪左、右齒面的單個齒距偏差不同,因此,對于同一齒輪的左、右齒面的單個齒距偏差 fp 應分開進行測量。
任一齒距累積偏差 Fpi是指 n 個相鄰齒距的理論弧長與實際弧長的代數差。n 的取值范圍為 1~ z(z 為被測齒輪的齒數) 。從理論上的定義來看,Fpi的數值即為這 n 個被測齒的任一單個齒距偏差的數值之和,也為選定 n 值之后的實際齒面到理論齒面之間的位移之差。齒距累積總偏差 Fp 指的是一個齒輪的所有齒在同一側齒面獲得的任一齒距累積偏差值之間的最大代數差。
對于數值 Fp 的正、負并沒有做出與之相應的規定; 此時,數值的正、負則由測量者所指定的測量方向 (逆時針或順時針) 來進行確定,如規定逆時針為負,順時針為正亦或是逆時針為正,順時針為負。對左、右齒面的 Fp 應單獨測量。
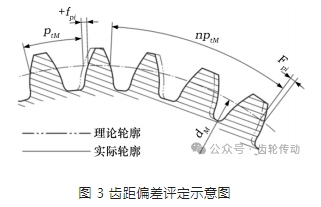
在 ISO 1328—1: 2013 中,對齒距偏差評定給出了示意圖,如圖 3 所示。圖 3 中,dM 為被測齒輪的分度圓直徑; z 為被測齒輪的齒數; n 為任意選取的齒數; ptM為被測齒輪的理論齒距值,PtM =πdM /z。
三、線結構光進行齒距偏差測量
該次測量采用由北京工業大學與哈爾濱精達測量儀器有限公司等單位聯合開發的基于對齒輪齒距偏差的測量,并結合線結構光測量技術的新型復合齒輪線結構光測量系統,其測量過程流程見圖 4。
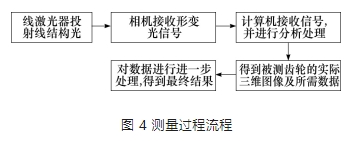
由圖 4 可知,進行齒輪齒距偏差的測量原理可以概括為: 線激光器發射出來的線結構光投射在齒輪表面; 通過平臺的移動,可以拾取到整個被測齒輪表面信息,由相機對相應的形變光信號進行采集; 計算機進行對應信息收集與處理; 得到被測齒輪實際三維圖像與所需數據; 將得到的實際齒廓與理論齒廓進行對比,通過計算分析即可得到被測齒輪的齒距偏差。
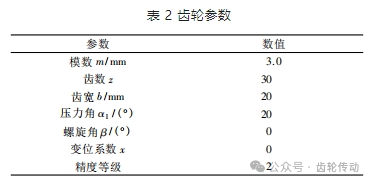
此次測量實驗選擇的齒輪為漸開線圓柱直齒齒輪樣板(被測齒輪) ,齒輪參數如表 2 所示。
被測齒輪三維模型如圖 5 所示。

線結構光測量設備如圖 6 所示。

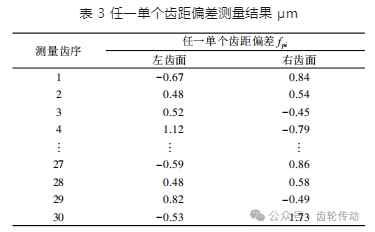
在線結構光測量系統中進行被測齒輪的齒距偏差測量,任一單個齒距偏差測量結果如表 3 所示。
經測量計算可得該被測齒輪左、右齒面任一齒距累積偏差,將其繪成曲線,分別如圖 7 和圖 8 所示。
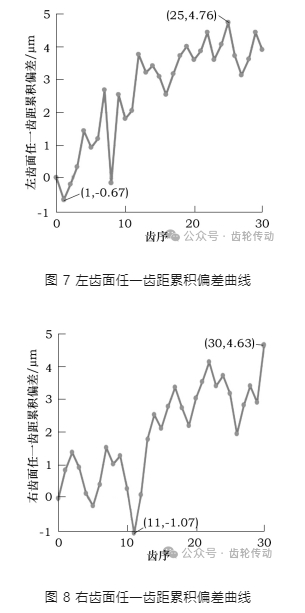
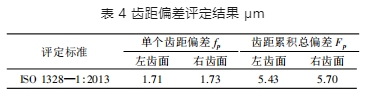
由圖 7 所示可知,左齒面任一齒距累積偏差在第 1 個齒達到最小值-0.67 μm,在第 25 個齒達到最大值 4.76 μm; 經計算,左齒面齒距累積總偏差為 5.43 μm。同理,由圖 8 所示可知,右齒面任一齒距累積偏差在第 11 個齒達到最小值-1.07 μm,在第 30 個齒達到最大值 4.63 μm; 經計算,右齒面齒距累積總偏差為 5.70 μm。經計算分析可得被測齒輪的齒距偏差評定結果,如表 4 所示。
由 ISO 1328—1: 2013 中齒距偏差許用值公式可知單個齒距偏差許用值 fpT為:
齒距累積總偏差許用值 FpT為:
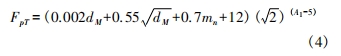
式中: dM 為被測齒輪的分度圓直徑( dM = mz) ; mn 為被測齒輪的法向模數(對于直齒輪而言,法向模數即為模數,即 mn = m) ; A1 為齒輪的精度等級。
由齒輪的參數可以求得該被測齒輪對應的 fpT為:
由齒輪的參數可以求得該被測齒輪對應的 FpT為:
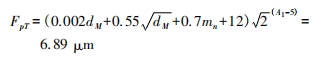
將被測齒輪的齒距偏差評定結果與偏差許用值進行對比可知,該齒輪的左、右齒面的單個齒距偏差分別為 1.71 μm 和 1.73 μm( 見表 4) ,均小于該齒輪的單個齒距偏差許用值 2.22 μm,所以該齒輪的單個齒距偏差達到 2 級精度; 該齒輪的左、右齒面的齒距累積總偏差分別為 5.43 μm 和 5.70 μm(見表 4) ,均小于該齒輪的齒距累積總偏差許用值 6.89 μm,所以該齒輪的齒距累積總偏差達到 2 級精度。
查 GB /T 10095.1—2008可知,模數為 3.0,齒數為 30,精度等級為 2 級的齒輪的單個齒距偏差的許用值范圍為-2.1 ~ 2.1 μm,當被測齒輪的單個齒距偏差的大小在許用值范圍之內,即代表該齒輪的單個齒距偏差達到了 2 級精度。由表 4 數據可以得知: 該齒輪的左、右齒面的單個齒距偏差數值均包含在對應的 2 級精度的許用值范圍之內,因此,該齒輪在單個齒距偏差上達到了對應 2 級精度的相關要求。
查 GB /T 10095.1—2008可知,模數為 3.0,齒數為 30,精度等級為 2 級的齒輪的齒距累積總偏差的許用值范圍為-6.5 ~ 6.5 μm,當被測齒輪的齒距累積總偏差的大小在許用值范圍之內,即代表該齒輪的齒距累積總偏差滿足了 2 級精度。由表 4 數據可以得知:該齒輪的左、右齒面的齒距累積總偏差數值均包含在 對應的 2 級精度的許用值范圍之內,因此,該齒輪在齒距累積總偏差上達到了對應 2 級精度的相關要求。
該漸開線圓柱直齒齒輪樣板通過高精度齒輪測量儀測量其左、右齒面的單個齒距偏差以及齒距累積總偏差,其測量結果為: 左、右齒面的單個齒距偏差分別為 1.7 μm 和 1.8 μm,左、右齒面的齒距累積總偏差分別為 5.7 μm 和 5.9 μm,均達到了對應 2 級精度的相關要求; 因此,通過對該漸開線圓柱直齒齒輪樣板的測量,證明該線結構光測量系統滿足超精密齒輪的測量要求。
四、結語
根據 ISO 1328—1: 2013《圓柱齒輪精度標準》對齒輪齒距偏差的定義,再結合當前非接觸式測量常用的幾種方法,從中選取了線結構光測量系統,對選定的漸開線圓柱直齒齒輪樣板的齒距偏差進行了測量,得到了該齒輪左、右齒面的單個齒距偏差分別為 1.71 μm 和 1.73 μm,以及其左、右齒面的齒距累積總偏差分別為 5.43 μm 和 5.70 μm,將其分別與 ISO 1328—1: 2013 和 GB /T 10095.1—2008 中對應的單個齒距偏差和齒距累積總偏差的許用值進行對比,證明了該線結構光測量系統能夠實現超精密齒輪的非接觸式測量,并為在機測量提供了一種新的參考。
參考文獻略.
