齒輪傳動具有傳動效率高、穩定性好、高可靠性等優點,是機械設備中最重要的傳動形式之一。常規直齒輪重合度較低,嚙合剛度突變程度較大,從而導致較大的振動噪聲,嚴重影響傳動系統的綜合性能。而細高齒齒輪通過采用大齒高設計來提高重合度及齒面接觸線長度,有效降低了嚙合剛度及嚙合力波動幅值,使得系統振動噪聲水平大幅下降,在提高齒輪承載能力的同時減輕了傳動裝置的體積質量,因此其在重卡變速器、直升機主減速器、軍用履帶式車輛及汽車電驅橋等領域得到了廣泛應用。但齒輪工作環境通常較為復雜,在交變載荷的長期作用下,齒根部位極易產生裂紋,若未及時采取措施,其在系統運行過程中將逐漸擴展,最終導致輪齒的疲勞斷裂,影響系統的可靠運行。因此研究細高齒齒輪在裂紋故障下的響應特性對保證傳動系統的安全平穩運行具有重要意義。
國內外學者針對裂紋故障齒輪系統開展了大量研究,取得了一定的成果。MA 等對含齒根裂紋直齒輪副的嚙合剛度進行研究,在傳統勢能法的基礎上計入齒廓修形、齒間耦合等影響因素。在此基礎上,HUANGFU 等考慮實際工況下裂紋沿齒寬及齒高方向的擴展形式,對含裂紋故障斜齒輪副的嚙合剛度計算模型進行修正。YANG 等研究了裂紋張開狀態對嚙合剛度及振動響應的影響,結果顯示在較大裂紋深度下,相比傳統計算模型其求解精度顯著提高。MENG、花志鋒等計入齒面摩擦的影響,利用集中質量模型對裂紋故障下系統的動態響應進行研究。QIAO 等在考慮真實裂紋擴展路徑的基礎上計入傳動軸柔性,分析了裂紋故障對齒輪系統振動響應的影響。LIU 等在簡化裂紋擴展模型的基礎上,引入新的故障程度評價指標,在建模過程中進一步考慮到箱體柔性對測點處振動響應的影響。DUAN 等將集中質量法、子結構法及有限元法相結合,建立了含齒根裂紋故障的行星齒輪系統剛柔耦合動力學模型,討論了齒圈厚度及邊界條件對系統動態響應的影響。以上研究均假設裂紋從齒根部位開始擴展,YANG 等采用勢能法對齒面裂紋故障下的時變嚙合剛度進行求解,分析了常用統計指標對故障演化的敏感程度。在上述單一故障研究的基礎上,CAO 等提出一種齒面磨損與齒根裂紋復合故障演化分析模型,采用集中質量法對復合故障模式下傳動系統的動態響應進行求解。以上研究對裂紋故障齒輪系統的剛度激勵及振動響應特性進行分析,且研究對象多為常規直齒輪。與常規直齒輪相比,細高齒齒輪重合度較大,在裂紋故障下其振動信號故障特征較為微弱。針對振動信號的不足,ZHANG 等提出采用齒根動應變作為故障特征載體信號,實現了基于內齒圈齒根應變的行星齒輪箱故障診斷。與振動信號相比,齒根應變與嚙合狀態之間具有更加直觀、明確的對應關系,理論上能更好地反映系統運行狀態。因此,研究裂紋故障下細高齒齒輪的齒根動應變,對細高齒齒輪系統的故障診斷具有重要意義。
本文建立了含裂紋故障的細高齒齒輪傳動系統動力學模型,結合輪齒承載接觸分析及有限元瞬態分析得到裂紋故障下細高齒齒輪的齒根動應變,分析裂紋深度對細高齒齒輪齒間載荷分配及齒根動應變的影響。
一、裂紋故障細高齒齒輪系統動力學模型
系統動力學模型
本文以一對外嚙合細高齒齒輪副為研究對象,其參數如表 1 所示。當齒輪副輸入轉速遠小于共振轉速,且負載轉矩較大時,齒側間隙及誤差對齒根動應變計算結果的影響較小,同時齒面摩擦對齒根應變的變化趨勢及數值的影響均較小。因此忽略上述各因素的影響,采用集中質量法建立系統動力學模型如圖 1 所示,其中 y 為嚙合線方向,P 為主動輪,G 為從動輪。
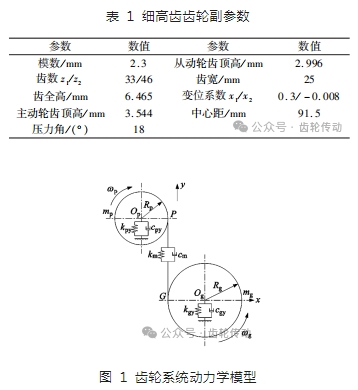
模型具有 4 個自由度,分別為主、從動輪轉動自由度 θp 、θg 及沿嚙合線方向的平移自由度 yp 、yg。以各彈簧受壓方向為正方向,則齒輪副動態嚙合力可表示為:
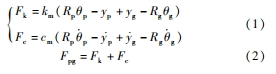
式中:Fk 為彈性嚙合力,Fc 為粘性嚙合力,Fpg為齒輪副動態嚙合力,Rp、Rg 分別為主、從動輪基圓半徑,km 為齒輪副時變嚙合剛度,cm 為齒輪副嚙合阻尼系數。
由 D′Alembert 原理可得系統動力學方程為:
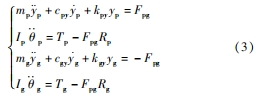
式中:mp 、mg 為主、從動輪質量,Ip 、Ig 為主、從動輪轉動慣量,kpy、kgy分別為主從動輪支撐剛度,cpy、cgy分別為主從動輪支撐阻尼。
裂紋故障齒輪副時變嚙合剛度
在從動輪齒根部位引入裂紋故障,采用三維建模軟件構建故障輪齒模型如圖 2a 所示,其中 y 軸為輪齒對稱軸方向,z 軸為齒寬方向。為研究裂紋深度對齒根動應變的影響,假設裂紋從齒根過渡圓角處沿直線方向進行擴展,且裂紋為影響到整個齒寬方向的貫通型裂紋,其中 q 為裂紋深度,分別取為 0.5、1、1.5 mm;d 為齒寬;v 為裂紋角度,其定義為裂紋擴展方向與輪齒對稱軸方向間的夾角,取為定值 45°。為準確求取裂紋故障下輪齒在載荷作用下的變形量,將輪齒從嚙入到嚙出的整個過程劃分為若干個嚙合位置,并假定齒輪材料滿足線彈性假設,采用有限元分析軟件對各嚙合位置建立分析模型如圖 2b 所示。
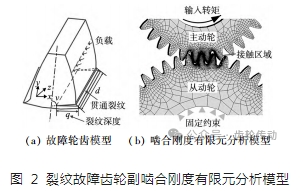
將從動輪內圈固定,在主動輪內圈施加轉矩 T 并約束各節點橫向自由度,定義嚙合齒面間的接觸,求解得到各嚙合位置處的主動輪轉角變形量 θ,則齒輪副沿嚙合線方向的變形量為:
式中:rb 為主動輪基圓半徑。
該嚙合位置的嚙合剛度為:
由式(5)求得不同裂紋深度下的齒輪副時變嚙合剛度如圖 3 所示。可以看出輪齒產生裂紋后齒根變軟,柔性增大,沿嚙合線方向的變形量增加,嚙合剛度減小,且隨著裂紋的加深,嚙合剛度降幅進一步增大。
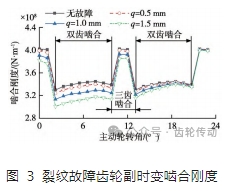
裂紋故障齒輪系統動態嚙合力
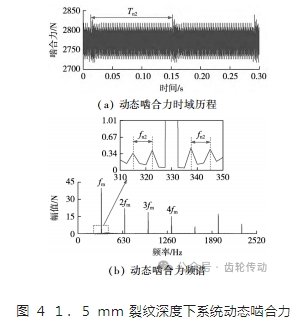
將圖 3 所示時變嚙合剛度代入系統動力學模型,采用 Newmark?β 法求解式(3)得到輸入轉速為 600 r/ min,輸入轉矩為 100 N·m 工況下含裂紋故障齒輪副的動態嚙合力。其中 1.5 mm 裂紋深度下的嚙合力時域歷程及頻譜如圖 4 所示。可以看到從動輪發生裂紋故障后,嚙合力時域歷程出現周期為 Tn2 = 1/fn2 的沖擊成分,嚙合力均值為 2 770.7 N,與靜載荷一致。在頻域中,齒輪副嚙合頻率及其倍頻附近出現邊頻帶,其間隔為從動輪轉頻 fn2。
二、裂紋故障下細高齒齒輪齒根動應變計算
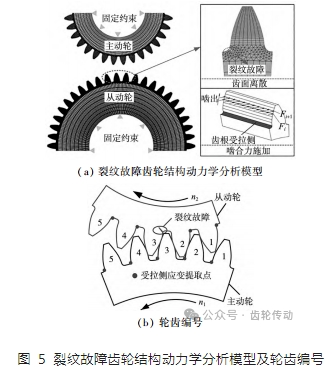
將嚙合齒面沿齒廓方向離散為 n 條接觸線,利用有限元分析軟件建立裂紋故障齒輪結構動力學分析模型如圖 5a 所示,其中參數 n 可根據計算精度要求確定。分析模型矩陣形式為:
式中:M 為齒輪結構質量矩陣,C 為齒輪結構阻尼矩陣,采用比例阻尼;K 為齒輪結構剛度矩陣,x(t)為節點位移列向量,F(t)為時變載荷列向量。
為便于后續分析,按圖 5b 所示方式對各輪齒進行編號,其中從動輪輪齒 3 為故障齒,輪齒 2 及輪齒 4 為其相鄰輪齒,輪齒 1 及輪齒 5 為其間隔輪齒。將主動輪中與從動輪故障齒相嚙合的輪齒記為輪齒 3,其余輪齒編號規則與從動輪一致。
將圖 4a 中的時域動態嚙合力進行離散,代入每一子步載荷后利用輪齒承載接觸分析方法得到齒間載荷分配關系。將離散后的每一子步載荷按輪齒載荷分配率分別施加到參與嚙合輪齒的各條接觸線上,從而模擬齒輪嚙合過程,最終利用有限元分析軟件中的瞬態分析模塊求解得到齒輪結構在時變嚙合力作用下的動態響應。其中輪齒載荷分配率的表達式為:

式中:Fij為 ti 時刻輪齒 j 所受載荷,Kij為 ti 時刻第 j 對嚙合輪齒的剛度,Ki 為 ti 時刻齒輪副嚙合剛度,ηij為 ti 時刻輪齒 j 的載荷分配率。
三、裂紋故障下細高齒齒輪齒根動應變分析
裂紋故障齒輪副輪齒載荷分配率
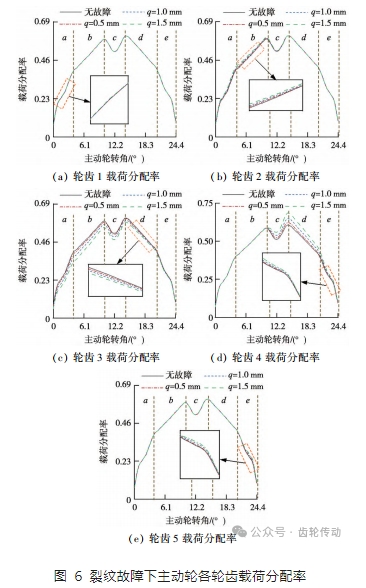
采用輪齒承載接觸分析方法得到裂紋故障下圖 5b 中主動輪各輪齒在 100 N·m 輸入轉矩及 600 r/ min 輸入轉速下的載荷分配率 ηij隨主動輪轉角的變化關系如圖 6 所示,其中 a、c、e 為三齒嚙合區,b、d 為雙齒嚙合區。可以看出從動輪發生裂紋故障后,故障齒剛度下降,其載荷分配率有所降低,如圖 6c 所示。當故障齒參與嚙合時,其相鄰輪齒的載荷分配率在三齒及雙齒嚙合區內均受到影響,而其間隔輪齒的載荷分配率僅在三齒嚙合區內發生變化,且三齒嚙合區載荷分配率變幅總體上小于雙齒嚙合區。同一嚙合位置下,隨著裂紋深度的增加,各輪齒載荷分配率變幅逐漸增大。由作用力及反作用力間的關系可知,從動輪各輪齒的載荷分配率與主動輪對應輪齒相同。
裂紋故障下從動輪齒根動應變分析
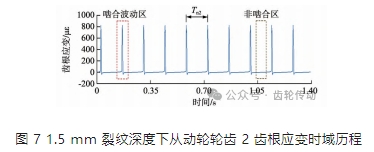
由前述動應變計算方法求解得到 1.5 mm 裂紋深度下圖 5b 中從動輪輪齒 2 在 100 N·m 輸入轉矩及 600 r/ min 輸入轉速下的齒根應變時域歷程如圖 7 所示。可以看到齒根應變呈周期性變化,無沖擊成分。
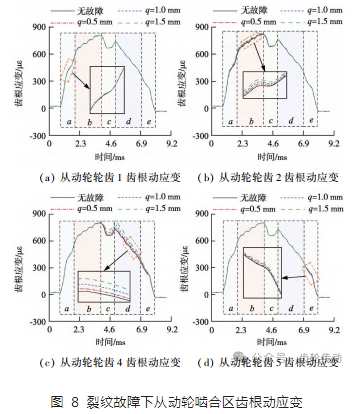
提取圖 5b 中從動輪除故障齒外輪齒嚙合區齒根動應變如圖 8 所示,其中區域 a、c、e 為三齒嚙合區,區域 b 和 d 為雙齒嚙合區。可以看出發生裂紋故障后,在嚙合力沖擊及載荷分配率變化的共同作用下,各輪齒所受載荷在部分嚙合區間內較無故障齒輪副有所增加,導致齒根應變在相應區間內有所增大,且各輪齒齒根動應變與圖 6 中載荷分配率的變化形式相似。其中從動輪輪齒 1 及輪齒 5 的齒根應變僅在區域 a 或 e 中略大于無故障齒輪副,而輪齒 2 和輪齒 4 的齒根應變在區域 b 或 d 內相比無故障齒輪副明顯增大,且在同一嚙合位置下,齒根應變增幅隨裂紋深度的增加呈上升趨勢。
裂紋故障下主動輪齒根動應變分析
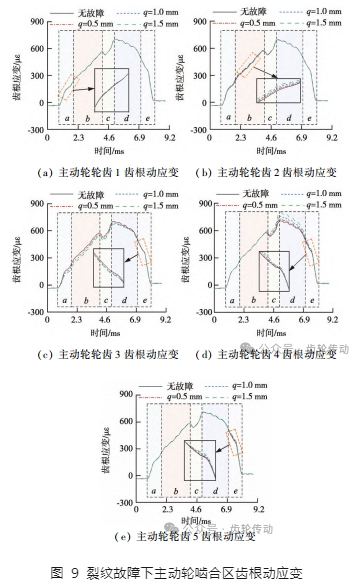
當故障齒與主動輪輪齒 3 相嚙合時,提取圖 5b 中主動輪輪齒 1 至輪齒 5 嚙合區齒根動應變如圖 9 所示。可以看出隨著嚙合過程的進行,作用于從動輪故障齒上的載荷有所降低,使得在整個嚙合區內,主動輪輪齒 3 的齒根應變與無故障條件下相比呈降低趨勢,但在嚙合力沖擊的作用下其降幅較小。除輪齒 3 外,其余輪齒齒根應變的變化趨勢與從動輪對應輪齒相似。當主動輪輪齒處于第二個三齒或雙齒嚙合區間時,其載荷作用點接近齒頂,力臂較大,在相同載荷增量作用下其齒根應變增幅較大,因此主動輪輪齒 4 及輪齒 5 的齒根應變增幅略大于從動輪相應輪齒。類似地,輪齒 1 及輪齒 2 的齒根應變增幅略小于從動輪對應輪齒。
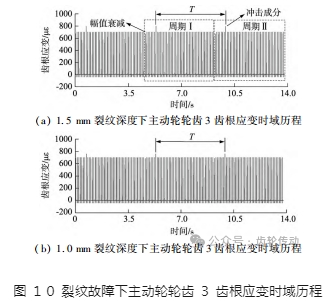
由于從動輪發生裂紋故障后主動輪各輪齒齒根應變時域歷程基本一致,此處以圖 5b 中主動輪輪齒 3 為例,分別提取 1.0 mm 及 1.5 mm 裂紋深度下該輪齒齒根應變時域歷程如圖 10 所示。可以看到當從動輪故障齒分別與圖 5b 中主動輪輪齒 4 及輪齒 3 相嚙合時,由圖 9 可知此時主動輪輪齒 3 齒根應變峰值將出現不同程度的增大或減小,導致齒根應變出現周期性沖擊及幅值衰減,且隨著裂紋深度的增加,上述現象愈明顯。其中周期 T 表達式為:
式中:z1 為主動輪齒數,z2 為從動輪齒數,n1 為主動輪轉速,LCM(z1 ,z2 )為 z1 與 z2 的最小公倍數。
裂紋故障下齒根應變信號統計指標分析
由于從動輪齒根動應變故障特征主要表現為嚙合區內齒根應變數值的變化,采用故障條件下嚙合區齒根應變均方根值較無故障條件下的相對變化量來評價裂紋對圖 5b 中從動輪各輪齒嚙合區齒根動應變的影響。齒根動應變均方根值表達式為:
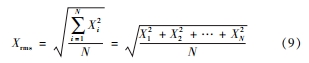
其相對變化量為:
式中:Xi 為 ti 時刻對應齒根動應變,N 為采樣點數,Xrc 為裂紋故障下齒根動應變均方根值,Xrh為無故障條件下齒根動應變均方根值。
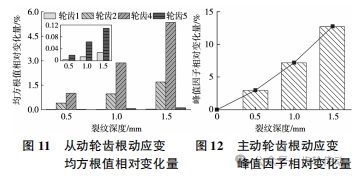
最終計算結果如圖 11 所示。可以看到在嚙合區內,齒根動應變均方根值隨裂紋深度的增加呈上升趨勢,且與故障齒相鄰輪齒的均方根值增幅明顯大于其間隔輪齒。當裂紋深度為 1.5 mm 時,從動輪嚙合區齒根應變均方根值相對變化量最高達到 5.34% 。
由于從動輪出現裂紋故障后,主動輪齒根應變時域歷程中將出現周期性沖擊成分,采用對沖擊較為敏感的峰值因子指標來評價裂紋對上述沖擊特征的影響。齒根動應變峰值因子表達式為:
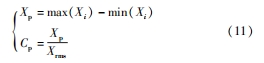
其相對變化量為:
式中:Xp 為齒根動應變峰峰值,Cp 為齒根動應變峰值因子,Cpc為裂紋故障下齒根動應變峰值因子,Cph為無故障條件下齒根動應變峰值因子。
最終計算結果如圖 12 所示。可以看到隨著裂紋深度的增加,齒根應變峰值因子呈上升趨勢。在 1.5 mm 裂紋深度下,主動輪齒根應變峰值因子相對變化量達到 12.72% 。從以上結果中可以看出與從動輪嚙合區齒根動應變均方根值相比,主動輪齒根動應變峰值因子指標對齒根裂紋故障表現出更強的敏感性。
四、結論
本文采用動力學分析、輪齒承載接觸分析與有限元瞬態分析相結合的方式計算了從動輪齒根裂紋故障下細高齒齒輪的齒根動應變,分析了裂紋深度對齒根動應變的影響,主要結論為:
(1)隨著嚙合過程的進行,從動輪故障齒載荷分配率逐漸減小,其相鄰輪齒齒根應變在三齒及雙齒嚙合區內均有所增加,其間隔輪齒齒根應變僅在三齒嚙合區內有所增大。
(2)主動輪齒根動應變故障特征主要表現為齒根應變時域歷程中出現周期性沖擊及幅值衰減現象,且裂紋深度越大,上述特征愈明顯。
(3)隨著裂紋深度的增加,從動輪故障齒的相鄰及間隔輪齒嚙合區齒根動應變均方根值及主動輪齒根動應變峰值因子均呈上升趨勢,且主動輪齒根動應變峰值因子指標對齒根裂紋故障表現出更強的敏感性;在 1.5 mm 裂紋深度下,主動輪齒根應變峰值因子相對變化量達到 12.72% 。
參考文獻略.
